
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственные интегралы от неограниченных функций
Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция f (x) терпит бесконечный разрыв (не существует): 1) в точке 2) точке 3) в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка. Если подынтегральной функции не существует в точке Рассмотрим сразу пример, чтобы было понятно:
Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, так как, если мы подставим в подынтегральную функцию значение нижнего предела
то знаменатель обращается в ноль, то есть подынтегральной функции в этой точке просто не существует! При анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел:
Здесь всё хорошо. Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода. Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна), либо несобственный интеграл равен конченому числу (когда площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению a справа. Легко проследить по чертежу, что по оси OX мы должны бесконечно близко приблизиться к точке разрыва справа. Посмотрим, как это реализуется на практике.
Пример 6 Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (a = 3/4). Проверяем, всё ли нормально с верхним пределом. Сначала вычислим неопределенный интеграл:
Выполняем замену переменных:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле.
Вычислим теперь несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела:
Добавка +0 обозначает, что мы стремимся к значению (3/4) оставаясь справа от него, что логично (см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница. (3) Разбираемся с А сейчас примеры для самостоятельного решения. Пример 7 Вычислить несобственный интеграл или установить его расходимость.
Пример 8 Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке b. Здесь всё делаем так же, за исключением того, что предел стремится к значению b слева. По оси OX мы должны бесконечно близко приблизиться к точке разрыва слева.
Пример 9 Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке b = 3; устно проверяем, что с другим пределом интегрирования всё нормально. Для разнообразия решим этот предел сразу – методом подведения функции под знак дифференциала. Те, кому трудно, могут сначала найти неопределенный интеграл по уже рассмотренной схеме.
Добавка (-0) обозначает, что предел у нас левосторонний, и к точке b =3 мы приближаемся по оси OX слева, оставаясь меньше 3. Разбираемся, почему дробь
(это лучше делать устно или на черновике). Подставляем под корень предельное значение b = 3 - 0.
и тогда
Окончательно:
Несобственный интеграл расходится. Знак минус обозначает, что соответствующая криволинейная трапеция расположена под осью OX. Будьте очень внимательны в знаках.
Да, конечно, здесь несобственный интеграл расходится, но И заключительные два примера для самостоятельного рассмотрения: Пример 10 Вычислить несобственный интеграл или установить его расходимость.
Пример 11 Вычислить несобственный интеграл или установить его расходимость.
Разбор ситуации, когда оба предела интегрирования «плохие», или точка разрыва содержится прямо на отрезке интегрирования, можно найти в статье Эффективные методы решения определённых и несобственных интегралов.
Решения и ответы: Пример 4: Решение:
Подынтегральная функция непрерывна на
Пример 5: Решение:
Подынтегральная функция непрерывна на
Несобственный интеграл расходится. Пример 7: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Несобственный интеграл расходится. Примечание: с пределом выражения
можно разобраться следующим образом: вместо
Пример 8: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Примечание: Разбираемся в пределе выражения
(см. график логарифмической функции!), тогда:
Именно эти соображения и помечаются, как
Пример 10: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке b = 1
Пример 11: Решение:
Подынтегральная функция терпит бесконечный разрыв в точке
Несобственный интеграл расходится Примечание: Разбираемся в пределе выражения
Если
Будьте очень внимательны в знаках!
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.187 (0.025 с.) |
 .
. ,
, ,
,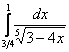 .
. ,
, .
.
 .
. .
. .
. .
. .
. при
при  , подставляем три четверти и указываем, что
, подставляем три четверти и указываем, что  . Причесываем ответ. В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью OX.
. Причесываем ответ. В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью OX. .
. .
. .
.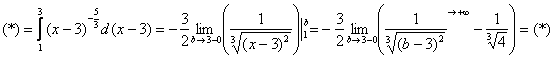
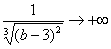

 .
.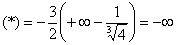 .
. и
и  – это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку.
– это разные вещи, разные жанры, и если Вы недосмотрите за знаками, то, строго говоря, допустите серьезную ошибку. .
. .
. .
. .
.
 .
. .
. .
.


 подставляем (-1)+0:
подставляем (-1)+0:



 . Если
. Если  , то
, то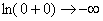
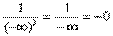 .
. .
.

 .
.
 .
.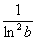 .
. , то
, то , и тогда
, и тогда .
.


