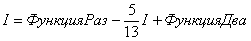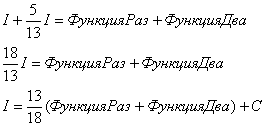Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра: Пример 5 Найти неопределенный интеграл
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе, не сложно. Если знаешь как. Обозначим рассматриваемый интеграл латинской буквой I и начнем решение:
Интегрируем по частям:
(1) Готовим подынтегральную функцию для почленного деления. (2) Почленно делим подынтегральную функцию. Возможно, не всем понятно, распишем подробнее:
(3) Используем свойство линейности неопределенного интеграла. (4) Берём последний интеграл («длинный» логарифм). Теперь смотрим на самое начало решения:
И на концовку:
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе! Приравниваем начало и конец:
Переносим I в левую часть со сменой знака:
А двойку сносим в правую часть. В результате:
Или: Константу C, строго говоря, надо было добавить ранее, но мы приписали её в конце. Настоятельно рекомендуем прочитать в примечании, в чём тут строгость:
Примечание: Более строго заключительный этап решения выглядит так:
Таким образом:
Константу В результате:
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях. Там будем строгими, особенно при определении частных решений. А здесь такая вольность допускается только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования. Пример 6 Найти неопределенный интеграл
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, или его часть, то решение в любом случае сводится к двум разобранным Примерам 5 и 6. Например, рассмотрим интеграл
Всё, что нужно сделать – это тождественными преобразованиями предварительно выделить полный квадрат:
Далее проводится линейная замена, которая обходится «без всяких последствий»:
Или такой пример, с квадратным двучленом: Выделяем полный квадрат: И, после линейной замены
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе: – интеграл от экспоненты, умноженной на синус; – интеграл от экспоненты, умноженной на косинус. В этих перечисленных интегралах по частям придется интегрировать уже два раза: Пример 7 Найти неопределенный интеграл
Подынтегральная функция – экспонента, умноженная на синус. Дважды интегрируем по частям и сводим интеграл к самому себе:
В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
Переносим
Готово. Попутно желательно причесать правую часть, т.е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:
За u мы обозначили экспоненту. Возникает вопрос, именно ли экспоненту всегда нужно обозначать за u? Не обязательно. На самом деле в рассмотренном интеграле принципиально без разницы, что обозначать за u, можно было пойти другим путём:
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании). То есть, за u можно обозначить и тригонометрическую функцию. Но, в рассмотренном примере это менее рационально, поскольку появятся дроби. При желании можете попытаться решить данный пример вторым способом, ответы обязательно должны совпасть. Пример 8 Найти неопределенный интеграл
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за u, экспоненту или тригонометрическую функцию? Полное решение и ответ в конце урока.
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например:
Попутаться в подобном интеграле придется многим. Дело в том, что в решении велика вероятность появления дробей, и очень просто что-нибудь по невнимательности потерять. Кроме того, велика вероятность ошибки в знаках, обратите внимание, что в показателе экспоненты есть знак «минус», и это вносит дополнительную трудность. На завершающем этапе часто получается примерно следующее:
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.149 (0.008 с.) |
 .
.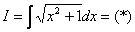 .
. .
. .
. .
.

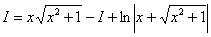

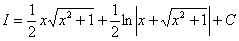

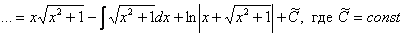
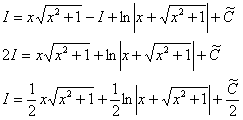
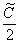 можно переобозначить через
можно переобозначить через  . Почему можно переобозначить? Потому что
. Почему можно переобозначить? Потому что 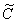 всё равно принимает любые значения, и в этом смысле между константами
всё равно принимает любые значения, и в этом смысле между константами 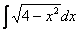 .
.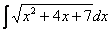 .
.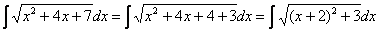 .
.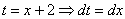 , в результате чего получается интеграл
, в результате чего получается интеграл 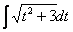 . Нечто знакомое, правда (см. Пример 5)?
. Нечто знакомое, правда (см. Пример 5)?

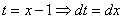 , получаем интеграл
, получаем интеграл 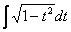 , который также решается по уже рассмотренному алгоритму.
, который также решается по уже рассмотренному алгоритму.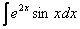 .
.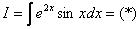
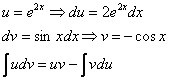

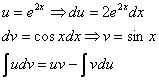

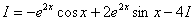
 в левую часть со сменой знака и выражаем наш интеграл:
в левую часть со сменой знака и выражаем наш интеграл:
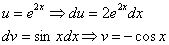
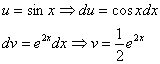 .
. .
.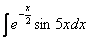 .
.