
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если сумма степеней косинуса и синуса – целое отрицательное число, тоинтеграл можно свести к тангенсам и его производной.
Для интеграла Для интеграла Для интеграла Рассмотрим пару более содержательных примеров на это правило:
Пример 20 Найти неопределенный интеграл
Сумма степеней синуса и косинуса
(1) Преобразуем знаменатель. (2) По известной формуле получаем (3) Преобразуем знаменатель. (4) Используем формулу
(5) Подводим функцию под знак дифференциала. (6) Проводим замену Далее берётся простой интеграл и проводится обратная замена.
Пример 21 Найти неопределенный интеграл
Это пример для самостоятельного решения.
Пример 22 Найти неопределенный интеграл
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
Пара творческих примеров для самостоятельного решения:
Пример 23 Найти неопределенный интеграл
Пример 24 Найти неопределенный интеграл
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока. Переходим к заключительному пункту путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет. Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл:
Считаем, что все эти числа и коэффициенты не равны нулю. В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции. Метод стар – необходимо избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить непростую замену. Замена, с помощью которой мы гарантированно избавимся от корня, такова:
Теперь нужно выразить «икс» и найти, чему равен дифференциал dx. Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения? Мы вывели готовые формулы, которыми можно пользовать при решении интеграла вида
Формулы замены таковы:
Заключительный пример: Пример 25 Найти неопределенный интеграл
Проведем замену:
В данном примере: a =-1, b = 2, c = 3, d = 1. Тогда для dx имеем:
Таким образом:
Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально
то обратно:
Преобразуем далее:
Некоторым страшно, а я это продифференцировал, ответ верный! Иногда встречаются интегралы вида
но это нужно быть либо слишком умным, либо попасть под раздачу. Идея та же – избавиться от корня, причем во втором случае, как все догадались, следует проводить подстановку
и самостоятельно выводить, чему будет равняться дифференциал dx. Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы: Пример 2: Решение:
Проведем замену:
Интегрируем по частям:
Пример 3: Ответ:
Пример 4: Ответ:
Пример 6: Решение:
Интегрируем по частям:
Таким образом:
В результате:
Пример 8: Решение: Дважды интегрируем по частям и сводим интеграл к самому себе:
Таким образом:
Пример 10: Решение:
Проведем замену:
Пример 11: Решение:
Замена:
Пример 12: Решение:
Замена:
Пример 14: Решение:
Дважды используем рекуррентную формулу
Пример 16: Решение:
Пример 18: Решение:
Используем формулу приведения:
и формулу двойного угла:
Далее имеем
Пример 19: Решение:
Пример 21: Решение: –3 – 3 = –6 – целое отрицательное число, значит преобразуем
Пример 23: Решение:
Пример 24: Решение:
Определенный интеграл. Примеры решений
Для того, чтобы научиться решать определенные интегралы необходимо: 1) Уметь находить соответствующие неопределенные интегралы.
2) Уметь вычислить определенный интеграл. Как видите, для того, чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому, если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще не совсем закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений. В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Нижний предел интегрирования стандартно обозначается буквой a. Верхний предел интегрирования стандартно обозначается буквой b. Отрезок [ a; b ] включает граничные точки и называется отрезком интегрирования. Что такое определенный интеграл? Можно посмотреть в учебниках про диаметр разбиения отрезка, предел интегральных сумм и т. д., но урок носит практический характер. Поэтому скажем, что определенный интеграл – это, прежде всего, самое что ни на есть обычное ЧИСЛО. Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача вычисления определённого интеграла – вычисление площади с помощью определенного интеграла. Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число, равное приращению первообразной функции на отрезке [ a; b ]. Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока. Этапы решения определенного интеграла следующие: 1) Сначала находим первообразную функцию F (X) (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле никогда не добавляется. Обозначение
Это подготовка для применения формулы Ньютона-Лейбница. 2) Подставляем значение верхнего предела в первообразную функцию: F (b). 3) Подставляем значение нижнего предела в первообразную функцию: F (a). 4) Рассчитываем (без ошибок!) разность F (b)- F (a), то есть, находим число, равное приращению первообразной (от подынтегральной) функции на отрезке [ a; b ]. Готово.
Всегда ли существует определенный интеграл? Нет, не всегда существует всё, что мы напишем в виде определённого интеграла. Например, интеграла
не существует, поскольку отрезок интегрирования
Такого интеграла тоже не существует на всём отрезке [-2; 3], так как в точках
этого отрезка подынтегральная функция f (x) = tg (x) не существует. Для того, чтобы определенный интеграл существовал на данном отрезке, необходимо, чтобы подынтегральная функция была непрерывной на отрезке интегрирования. Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. Бывает так, что подолгу мучаешься с нахождением трудной первообразной, а когда наконец-то ее находишь, то ещё и ломаешь голову над вопросом: «что за ерунда получилась?». Например, если получилось примерно так:
то нельзя подставлять отрицательные числа под корень! Если для решения в контрольной работе, на зачете или экзамене Вам предложен несуществующий интеграл вроде
то нужно дать ответ, что интеграла не существует и обосновать – почему. Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция. Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике. Интеграл
преспокойно вычисляется по формуле Ньютона-Лейбница. Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием
целесообразно поменять пределы интегрирования на «привычный» порядок:
В таком виде интегрировать значительно удобнее. Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
Это справедливо не только для двух, но и для любого количества функций. В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим. Для определенного интеграла справедлива формула интегрирования по частям:
Пример 1 Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла. (2) Интегрируем по таблице с помощью самой популярной формулы
(3) Используем формулу Ньютона-Лейбница
Сначала подставляем в x 3 верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2 Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Пример 3 Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла. (2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница. СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряем на третьем слагаемом:
т. к. очень часто машинально пишут
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, так:
Здесь устно использованы правила линейности, устно проинтегрированы табличные интегралы. Получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию мы сначала подставили 4, затем –2, опять же выполнив все действия в уме. При втором способе существует повышенный риск допустить ошибку в вычислениях, поэтому студенту-чайнику лучше использовать первый способ, чтобы не терять знаки. Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная.
находится в одной скобке.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.98 (0.096 с.) |
 – целое отрицательное число.
– целое отрицательное число. – целое отрицательное число.
– целое отрицательное число. – целое отрицательное число.
– целое отрицательное число. .
. : 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
: 2 – 6 = –4 – целое отрицательное число, значит, интеграл можно свести к тангенсам и его производной:
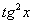 .
. .
. . Более опытные студенты замену могут и не проводить, но все-таки лучше заменить тангенс одной буквой – меньше риск запутаться.
. Более опытные студенты замену могут и не проводить, но все-таки лучше заменить тангенс одной буквой – меньше риск запутаться. .
. .
. .
.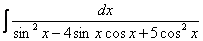 .
. .
. , где a, b, c, d – числа.
, где a, b, c, d – числа. .
.

 .
. .
. .
. .
. .
.

 .
.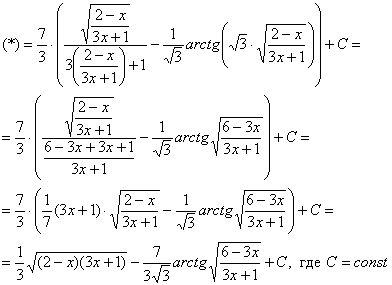 .
. ,
,  ,
, .
. .
.



 .
. .
.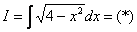 .
.









 .
.




 .
.
 .
.







 .
.
 .
.



 .
.
 .
. является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись
является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ?
?
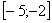 не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример:
не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример: .
. ,
, 
 ???!!!
???!!!

 .
.

 .
. .
.
 .
.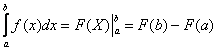 .
. .
. .
. .
. ,
, .
. .
.




