
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и относительная погрешности вычисленийСодержание книги
Поиск на нашем сайте Абсолютная погрешность вычислений находится по формуле:
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону. Относительная погрешность вычислений находится по формуле:
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без умножения на 100%, но на практике почти всегда используют вышеприведенный вариант с процентами.
После короткой справки вернемся к нашей задаче, в которой мы вычислили приближенное значение функции Вычислим точное значение функции с помощью микрокалькулятора:
Вычислим абсолютную погрешность:
Вычислим относительную погрешность:
Ответ: Следующий пример для самостоятельного решения:
Пример 4 Вычислить приближенно с помощью дифференциала значение функции Примерный образец чистового оформления и ответ в конце урока. Многие обратили внимание, что во всех рассмотренных примерах фигурируют корни. Это не случайно, в большинстве случаев в рассматриваемой задаче действительно предлагаются функции с корнями. Но для страждущих читателей я раскопал небольшой пример с арксинусом:
Пример 5 Вычислить приближенно с помощью дифференциала значение функции Этот коротенький, но познавательный пример тоже для самостоятельного решения.
Теперь рассмотрим особое задание: Пример 6 Вычислить приближенно с помощью дифференциала Решение: Что нового в задании? По условию требуется округлить результат до двух знаков после запятой. Но дело не в этом, школьная задача округления, думаю, не представляет для вас сложностей. Дело в том, что у нас дан тангенс с аргументом, который выражен в градусах. Что делать, когда вам предлагается для решения тригонометрическая функция с градусами? Например, Алгоритм решения принципиально сохраняется, то есть необходимо, как и в предыдущих примерах, применить формулу Записываем очевидную функцию Значение Анализируя таблицу, замечаем «хорошее» значение тангенса, которое близко располагается к 47 градусам, а именно:
После предварительного анализа градусы необходимо перевести в радианы. Так, и только так!
В данном примере непосредственно из тригонометрической таблицы можно выяснить, что
Таким образом: Ответ:
Пример 7 Вычислить приближенно с помощью дифференциала Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как видите, ничего сложного, градусы переводим в радианы и придерживаемся обычного алгоритма решения.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 , или, то же самое:
, или, то же самое:
 с помощью дифференциала.
с помощью дифференциала. , строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
 , получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение. , относительная погрешность вычислений
, относительная погрешность вычислений  .
. в точке
в точке 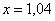 . Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
. Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений. ; в точке
; в точке  .
. , результат округлить до двух знаков после запятой.
, результат округлить до двух знаков после запятой. и т. д.
и т. д.

 нужно представить в виде
нужно представить в виде  . Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики.
. Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики. . Таким образом:
. Таким образом:  .
.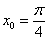 . По формуле перевода градусов в радианы:
. По формуле перевода градусов в радианы:  (формулы можно найти в той же таблице). Дальнейшее шаблонно:
(формулы можно найти в той же таблице). Дальнейшее шаблонно: .
. (при вычислениях используем значение
(при вычислениях используем значение 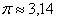 ). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
). Результат, как и требовалось по условию, округлён до двух знаков после запятой. .
. , результат округлить до трёх знаков после запятой.
, результат округлить до трёх знаков после запятой.


