
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложные производные. Логарифмическая производная. Производная степенно-показательной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Продолжаем повышать свою технику дифференцирования. На данном уроке мы закрепим пройденный материал, рассмотрим более сложные производные, а также познакомимся с новыми приемами и хитростями нахождения производной, в частности, с логарифмической производной. Тем читателям, у кого низкий уровень подготовки, следует обратиться к статье Как найти производную? Примеры решений, которая позволит поднять свои навыки практически с нуля. Далее необходимо внимательно изучить страницу Производная сложной функции, понять и прорешать все приведенные мной примеры. Данный урок логически третий по счету, и после его освоения Вы будете уверенно дифференцировать достаточно сложные функции. Нежелательно придерживаться позиции «Куда еще? Да и так хватит!», поскольку все примеры и приёмы решения взяты из реальных контрольных работ и часто встречаются на практике. Начнем с повторения. На уроке Производная сложной функции мы рассмотрели ряд примеров с подробными комментариями. В ходе изучения дифференциального исчисления и других разделов математического анализа – дифференцировать придется очень часто, и не всегда бывает удобно (да и не всегда нужно) расписывать примеры очень подробно. Поэтому мы потренируемся в устном нахождении производных. Самым подходящими «кандидатами» для этого являются производные простейших из сложных функций, например:
По правилу дифференцирования сложной функции
При изучении других тем матана в будущем такая подробная запись чаще всего не требуется, предполагается, что студент умеет находить подобные производные на автомате. Представим, что в 3 часа ночи раздался телефонный звонок, и приятный голос спросил: «Чему равна производная тангенса двух икс?». На это должен последовать почти мгновенный и вежливый ответ:
Первый пример будет сразу предназначен для самостоятельного решения. Пример 1 Найти следующие производные устно, в одно действие, например:
Ответы в конце урока
Сложные производные
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой. Пример 2 Найти производную функции Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, 1) Сначала нам нужно вычислить выражение 2) Затем необходимо вычислить логарифм: 3) Далее косинус: 4) Потом косинус возвести в куб: 5) На пятом шагу разность: 6) И, наконец, самая внешняя функция – это квадратный корень: Формула дифференцирования сложной функции
Вроде без ошибок…. (1) Берем производную от квадратного корня. (2) Берем производную от разности, используя правило (3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба). (4) Берем производную от косинуса. (5) Берем производную от логарифма. (6) И, наконец, берем производную от самого глубокого вложения Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает. Следующий пример для самостоятельного решения.
Пример 3 Найти производную функции Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения Полное решение и ответ в конце урока. Настало время перейти к чему-нибудь более компактному и симпатичному. Пример 4 Найти производную функции Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм. В таких случаях необходимо последовательно применить правило дифференцирования произведения Фокус состоит в том, что за «у» мы обозначим произведение двух функций:
Теперь осталось второй раз применить правило
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять. Готово.
Рассмотренный пример можно решить вторым способом: Оба способа решения абсолютно равноценны.
Пример 5 Найти производную функции Это пример для самостоятельного решения, в образце он решен первым способом. Рассмотрим аналогичные примеры с дробями.
Пример 6 Найти производную функции Здесь можно пойти несколькими путями:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную. Более простой пример для самостоятельного решения:
Пример 7 Найти производную функции Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8 Найти производную функции Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул. Само решение можно оформить примерно так: Преобразуем функцию: Находим производную: Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить». А сейчас пара несложных примеров для самостоятельного решения:
Пример 9 Найти производную функции
Пример 10 Найти производную функции
Все преобразования и ответы в конце урока.
Логарифмическая производная
Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.
Пример 11 Найти производную функции Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела. Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:
Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:
Собственно приступаем к дифференцированию.
Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться. Как быть с левой частью? В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?». Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции
В левой части как по мановению волшебной палочки у нас «нарисовалась» производная
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие: Окончательный ответ:
Пример 12 Найти производную функции Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока. С помощью логарифмической производной можно было решить любой из примеров №№4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


 :
:
 .
.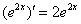 . Для выполнения задания нужно использовать только таблицу производных элементарных функций (если она еще не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции.
. Для выполнения задания нужно использовать только таблицу производных элементарных функций (если она еще не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 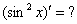 ,
,  ,
, ,
, 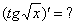 ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
, 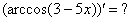

 и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение». , значит, сумма
, значит, сумма  – самое глубокое вложение.
– самое глубокое вложение.








 два раза
два раза , а за «вэ» – логарифм:
, а за «вэ» – логарифм:  . Почему так можно сделать? А разве
. Почему так можно сделать? А разве  – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
– это не произведение двух множителей и правило не работает?! Ничего сложного нет:
 :
:



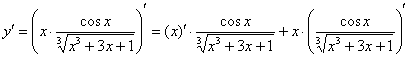

 , приняв за
, приняв за  весь числитель:
весь числитель: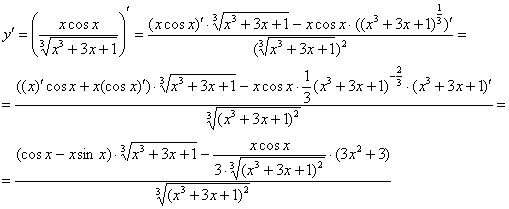

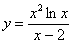


 , а потом ещё и от дроби
, а потом ещё и от дроби  .
.


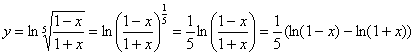



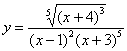





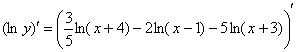

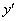 . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
. Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:





