
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простые и составные высказыванияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Есть два вида высказываний: 1) простые и 2) составные, или сложные. Под простым высказыванием будем понимать такое высказывание, которое не может быть разбито на более простые высказывания. Высказывания А и В предыдущего примера – простые высказывания. Про простое высказывание всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи так называемых логических связок или логических операций, например, союзов «и», «или», слов «если…, то…», «тогда и только тогда, когда…», можно строить сложные высказывания. Например, из высказываний
Отметим, что сложные высказывания можно образовывать и из таких высказываний, которые не связаны между собой по смыслу. Например, высказывание:
составлено при помощи логической операции «если…, то…» из двух высказываний, между которыми нет никакой смысловой связи. Сложные высказывания, как и простые, всегда или только истинны, или только ложны. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки (операции) использованы для образования сложного высказывания. Во-вторых, истинность или ложность сложного высказывания определяется тем, какие из простых высказываний, образующих сложное высказывание, истинны, а какие – ложны.
Логические операции Операции над высказываниями – логические операции – обычно задают в виде таблиц, называемых таблицами истинности. Операция отрицания, или отрицание высказывания Для каждого высказывания А может быть сформировано новое высказывание
Таблица истинности для операции отрицания:
Операция отрицания – одноместная, или унарная, операция. Последующие операции – двухместные, или бинарные. Например, если
Отметим, что если
Операция конъюнкции, или конъюнкция высказываний Высказывание С, составленное из двух высказываний А и В при помощи союза «и», называют конъюнкцией (логическим произведением) этих высказываний: Логическое произведение Таблица истинности для операции конъюнкции:
Пусть, например, Операцию конъюнкции можно определить и для нескольких высказываний, как связку высказываний, объединённых союзом «и». Конъюнкция из n высказываний – новое высказывание, причём высказывание А = имеет значение «истина», если и А 1, и А 2, и … Аn одновременно истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например, А 1 А 2 Ù А 3 Ù А 4 А 1 Ù А 3 Ù А 4
Операция дизъюнкции, или дизъюнкция высказываний Высказывание С, составленное из двух высказываний А, В при помощи союза «или», называют дизъюнкцией (логической суммой) этих высказываний: Сумма
Таблица истинности для операции дизъюнкции:
Пусть, например, Операцию дизъюнкции можно определить и для нескольких высказываний как связку высказываний, объединённых союзом «или»: А = В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Операция эквивалентности, или эквивалентность высказываний. Высказывание С, составленное из двух высказываний А и В при помощи слов «тогда и только тогда, когда…», называют эквивалентностью высказываний А и В: Для эквивалентности используют знак Эквивалентность Таблица истинности для операции эквивалентности:
Пусть Высказывание Операция импликации, или импликация высказываний Высказывание С, составленное из высказываний А и В при помощи слов «если…, то…», называют импликацией высказываний А и В и 1б1-начают (выражение Импликация Таблица истинности для операции импликации:
Первый член импликации Обратите внимание, что таблица истинности для импликации, в отличии от таблиц для конъюнкции, дизъюнкции и эквивалентности, изменяется при перестановке столбцов для А и В. Отметим также, что импликация не полностью соответствует обычному пониманию слов «если…, то…» и «следует». Из третьей и четвёртой строк таблицы истинности для импликации вытекает, что если А – ложно, то, каково бы ни было В, высказывание Например, утверждение «если 6 – простое число, то Как говорил Р. Декарт: «Если 2 х 2 = 5, то я докажу, что из трубы вылетает ведьма».
Для иллюстрации содержательного смысла импликации рассмотрим ещё один пример. Пусть
Импликация «если папа завтра получит премию, то купит сыну велосипед». Пусть А и В – истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Если же папа, получив премию (А – истинно), не купит сыну велосипед (В – ложно), то это, можно сказать, – не логичный поступок, и импликация имеет значение «ложь». Если папа не получит премию (А – ложно), но купит велосипед (В – истинно), то результат положителен (импликация истинна). Наконец, в том случае, если, не получив премии (А – ложно), папа не купит велосипед (В – ложно), то обещание не нарушено, импликация истинна.
Задача 1. Даны два высказывания Решение. 1) Высказывание 2) Высказывание Высказывание 3) Эквивалентность ( 4) Импликация В самом деле, импликация
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 3051; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.203.242 (0.011 с.) |

 ;
;  , используя логические операции, можно образовать следующие сложные высказывания:
, используя логические операции, можно образовать следующие сложные высказывания: ,
, ,
,
 .
. {если слон – насекомое, то Антарктида покрыта тропическими лесами}
{если слон – насекомое, то Антарктида покрыта тропическими лесами} (читается «не А», или «не верно, что А») – это отрицание высказывания А. Высказывание
(читается «не А», или «не верно, что А») – это отрицание высказывания А. Высказывание  - истинное высказывание, то
- истинное высказывание, то - ложное высказывание (отрицание А).
- ложное высказывание (отрицание А). {в комнате холодно}, то
{в комнате холодно}, то  {в комнате не холодно}, но при этом высказывание
{в комнате не холодно}, но при этом высказывание 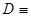 {в комнате жарко} отрицанием высказывания В не является.
{в комнате жарко} отрицанием высказывания В не является. (выражение
(выражение  читается: «А и В»).
читается: «А и В»). истинно только в том случае, когда: «и А, и В одновременно истинны».
истинно только в том случае, когда: «и А, и В одновременно истинны». ,
,  . Тогда высказывание С – истинно, т. к. истинно каждое из высказываний А и В, составляющих высказывание С.
. Тогда высказывание С – истинно, т. к. истинно каждое из высказываний А и В, составляющих высказывание С. Аi; где i = 1; 2; …; n
Аi; где i = 1; 2; …; n , А 2
, А 2  , А 3
, А 3  , А 4
, А 4  . Тогда высказывание
. Тогда высказывание {(8 = 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – ложное, в то время как высказывание
{(8 = 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – ложное, в то время как высказывание (выражение
(выражение  читается: «А или В»).
читается: «А или В»).
 ,
,  . Тогда высказывание
. Тогда высказывание  или
или  – истинно, т.к. истинно каждое из высказываний А и В, составляющих высказывание С.
– истинно, т.к. истинно каждое из высказываний А и В, составляющих высказывание С. Аi; где i = 1; 2; …; n
Аi; где i = 1; 2; …; n .
. (или ~).
(или ~). {число 3n является чётным},
{число 3n является чётным},  {число 3n является чётным тогда и только тогда, когда n – чётное число} есть эквивалентность высказываний А и В:
{число 3n является чётным тогда и только тогда, когда n – чётное число} есть эквивалентность высказываний А и В:  .
.
 читается «из А следует В», или «если А, то В»).
читается «из А следует В», или «если А, то В»).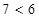 », или утверждение «если
», или утверждение «если  и
и  . В чём заключаются высказывания
. В чём заключаются высказывания  ,
,  ,
,  ,
,  ? Какие из этих высказываний истинны и какие ложны?
? Какие из этих высказываний истинны и какие ложны? , очевидно, ложно. Для того чтобы произведение двух высказываний было истинным, нужно чтобы оба высказывания были истинными.
, очевидно, ложно. Для того чтобы произведение двух высказываний было истинным, нужно чтобы оба высказывания были истинными. истинно, т.к. одно из слагаемых является истинным высказыванием.
истинно, т.к. одно из слагаемых является истинным высказыванием. .
.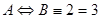 тогда и только тогда, когда
тогда и только тогда, когда  ) представляет собой ложное высказывание, т.к. А – ложно, а В – истинно.
) представляет собой ложное высказывание, т.к. А – ложно, а В – истинно. то
то 


