
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула применяется слева направоСодержание книги
Поиск на нашем сайте
Смотрим на левую часть: В интегралах рассматриваемого типа за u всегда обозначается логарифм. Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за u мы обозначили логарифм, а за dv – оставшуюся часть подынтегрального выражения. Следующий этап: находим дифференциал du:
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках. Теперь находим функцию v. Для того чтобы найти функцию v необходимо проинтегрировать правую часть нижнего равенства dv = dx:
Теперь открываем наше решение и конструируем правую часть формулы: Вот кстати, и образец чистового решения с небольшими пометками:
Единственный момент, в произведении uv я сразу переставил местами u и v, так как множитель x принято записывать перед логарифмом. Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам. Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом, обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс». Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно. В ходе проверки мы использовали правило дифференцирования произведения: Формула интегрирования по частям
Пример 2 Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен. Решаем.
Мы еще один раз подробно распишем порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока. Как уже говорилось, за u необходимо обозначить логарифм (то, что он в степени – значения не имеет). За dv обозначаем оставшуюся часть подынтегрального выражения. Записываем в столбик:
Сначала находим дифференциал du:
Здесь использовано правило дифференцирования сложной функции
Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений мы акцентировали внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз. Теперь находим функцию v, для этого интегрируем правую часть нижнего равенства
Для интегрирования мы применили простейшую табличную формулу
Теперь всё готово для применения формулы
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за u в похожих ситуациях всегда обозначается логарифм.
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке (2) Раскрываем скобки. Последний интеграл упрощаем. (3) Берем последний интеграл. (4) «Причесываем» ответ. Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3 Найти неопределенный интеграл
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! Можете также попробовать взять его по частям, получится забавная вещь.
Пример 4 Найти неопределенный интеграл
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
В примерах 3, 4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.132.118 (0.011 с.) |

 . Очевидно, что в нашем примере
. Очевидно, что в нашем примере  (и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за u, а что-то за dv.
(и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за u, а что-то за dv.


 .
.

 . И это не случайно.
. И это не случайно. и формула
и формула  .
.

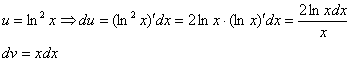
 .
. :
:
 .
. :
:
 .
.
 , и эти скобки нужно корректно раскрыть.
, и эти скобки нужно корректно раскрыть. .
. .
.


