
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение системы по правилу КрамераСодержание книги
Поиск на нашем сайте
Ранее мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Далее разберём правило Крамера и решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Для того, чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите раздел Вычисление определителей. Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения! Во-первых, пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными. Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера! Рассмотрим систему уравнений
На первом шаге вычислим определитель, который называют главным определителем системы.
Если
На практике вышеуказанные определители также могут обозначаться латинской буквой D с соответствующими индексами. Корни уравнения находим по формулам:
Пример 7: Решить систему линейных уравнений
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – редкий гость в практических заданиях по математике, эту систему мы взяли из эконометрической задачи. Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби. Что делать? В подобных случаях и приходят на помощь формулы Крамера. Прежде всего, вычислим определитель системы:
значит, система имеет единственное решение. Вычислим ещё два определителя:
Как видите, корни получились иррациональными, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики. Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс.
Когда используете данный метод, обязательным фрагментом оформления задания является следующий: «Δ ≠ 0, значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теореме Крамера. Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения
Пример 8: Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
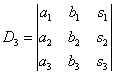
Находим главный определитель системы: Если D ≠ 0, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
И, наконец, ответ рассчитывается по формулам: Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два». Здесь столбец свободных членов Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по такому же принципу.
Пример 9: Решить систему по формулам Крамера.
Решение: Вычислим определитель системы
Ответ:
Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная
Здесь на месте отсутствующих переменных ставятся нули.
Примечание: Определители рационально раскрывать по той строке (столбцу), в которой есть ноль, или максимальное число нулей, так как вычислений получается меньше.
Пример 10:
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (ответ в конце урока).
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.231 (0.008 с.) |

 .
. .
. , то система имеет бесконечно много решений или не имеет решений (несовместна). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса. Если
, то система имеет бесконечно много решений или не имеет решений (несовместна). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса. Если  , то система имеет единственное решение, и для нахождения двух неизвестных мы должны вычислить еще два определителя:
, то система имеет единственное решение, и для нахождения двух неизвестных мы должны вычислить еще два определителя: и
и  .
. ,
,  .
. .
. ,
, ;
;
 ;
;  Ответ:
Ответ:  ,
, 


 . Если D = 0, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
. Если D = 0, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса. ,
,  ,
, 
 ,
,  ,
,  .
. последовательно «прогуливается» слева направо по столбцам главного определителя.
последовательно «прогуливается» слева направо по столбцам главного определителя. .
.
 , - значит, система имеет единственное решение.
, - значит, система имеет единственное решение.





 .
.
 , во втором – переменная
, во втором – переменная 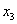 . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель, в данном случае он имеет вид:
. В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель, в данном случае он имеет вид: .
.



