
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие производной функции, ее геометрический смысл.Содержание книги
Поиск на нашем сайте Производной функции y’(x), f’(x) называетсяпредельное значение приращения функции к приращению аргумента Геометрический смысл-tg угла наклона касательной к графику функции. Правая и левая производные. Правой(левой) производной функции y=f(x) называется правое(левое) предельное значение отношения приращения функции F’(x+0) правая производная, F’(x-0) левая производная.
Дифференцируемость функции(определение. Теорема26). Функция называется дифференцируемой в т. X, если ее приращение Δy (в этой точке), соответствующее приращению аргумента Δx, равно Δy=A* Δx+o(Δx) не зависит от Δx. Для того, чтобы функция была дифференцируемой в точке x0 необходимо и достаточно, чтобы она имела этой точке конечную производную. Необходимость-считается, что функция дифференцируема в точке x0. Надо доказать, что она имеет в этой точке производную. По определению дифференциала функции Δy= Достаточность-считается,что в т. x0 существует конечная производная. Надо доказать, что в x0 функция дифференцируема. По определению производной Дифференциал функции. Дифференциалом функции dy в точке x0 называется главное приращение функции в этой точке dy=y’(x)*dx Правила дифференцирования суммы, разности, произведения частного(теорема27). Пусть функции u(x) и g(x) дифференцируемы в точке x. Тогда сумма, разность, произведение, частное(при условии, что знаменатель ≠0 в точке x) этих функций также дифференцируемы. При этом справедливы формулы: 1. 2. 3. Дифференцирование обратной функции(теорема28) Пусть функция y=f(x) дифф. в точке x0 и пусть в окрестности этой точки y=f(x) имеет обратную функцию x=f-1(y). Тогда обратная функция дифф. в точке y0 =f(x0)(соответствует т. X0) и справедлива формула: Док-во. Возьмем некоторое приращение аргумента y, т.е.
Производные показательной и обратных тригонометрических функций. 1. y=ax (a>0, a≠0, x (-∞, +∞)) x=logay обратная функция. y’=[ax]x’= 2. y=arcsinx (x [-1, 1], y [ 3. Y=arctg x; (x (-∞, ∞), y ( Правило дифференцирования сложной функции(теорема29). Рассмотрим сложную функцию вида y=f(g(x)). Пусть функция g(x) дифференцируема в точке x0 , а функция f(g) дифференцируема в точке g0=g(x). Тогда сложная функция y=f(g(x)) дифференцируема в точке x0 , при этом справедлива формула Логарифмическая производная. Пусть функция y=f(x) дифференцируема в точке x и положительна в ней. Тогда имеет смысл равенство ln y=ln f(x), (ln y)’=(ln(f(x)))’ => Использование дифференциала для приближенных вычислений. Пусть функция y=f(x) дифференцируема в точке x0, тогда приращение Δy=f’(x) Производные и дифференциалы высших порядков. Формула Лейбница. Пусть функция y=f(x) дифференцируема в точке x, тогда y’=f’(x)=g(x). Если g(x) дифференцируема в той же точке, можно записать g’(x)=[f’(x)]’=f’’(x). Рассуждая аналогично, можно ввести поняти3,4,… n-порядок производных. Для производной n-го порядка принято следующее обозначение y(n)=f(n)(x). Формула Лейбница. Y=u(x)*v(x). (uv)(n)= Дифференциал высшего порядка. Пусть функция y=f(x) дифференцируема в точке x. dy=f’(x)dx. Если функция f’(x) дифференцируема, то можно записать d(dy)=d2y=d(f’(x)dx)=d(f’(x)dx=f’’(x)dxdx=f’’(x)(dx)2 Если функция n-раз дифференцируема, то можно записать dny=f(n)(x)(dx)n=f(n)(x)= Дифференцирование функции, заданной параметрически. Правило Лопиталя(теорема30). Пусть функция f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x0, пусть кроме того, Формула Тейлора(теорема31). Пусть функция у=f(x) дифференцируема n-раз в точке x0 и некоторой окрестности этой точки. Тогда для любой точки x из этой окрестности справедлива формула: f(x)=f(x0)+ В форме Пеана o((x-x0)’), в форме Лагранжа Частный вид формулы Тейлора при x0 носит название формулы Маклорена.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

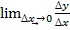

 =>
=>  =A+
=A+  ,
,  =A+
=A+  =A, y’(x0)=A. Δy0=y’(x0)+o(
=A, y’(x0)=A. Δy0=y’(x0)+o( )
) =f’(x), тогда
=f’(x), тогда  = α(
= α( ,
,  =y’(x0)*
=y’(x0)*  +o(x)
+o(x) .
.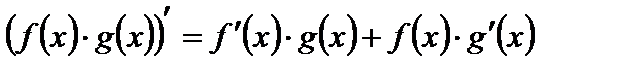 .
. .
.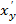 (y0)=
(y0)=  =
= 
 0. Тогда соответствующее приращение
0. Тогда соответствующее приращение  (в силу строгой монотонности обратной функции). Производная обратной функции
(в силу строгой монотонности обратной функции). Производная обратной функции 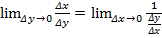 =
=  =
=  =
=  =ylna=axlna
=ylna=axlna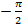 ,
,  ]) x=siny, y’=[arcsinx]’=
]) x=siny, y’=[arcsinx]’=  =
= 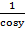 . Используя основное тригонометрическое тождество: sin2y+cos2y=1 => cosy=+-
. Используя основное тригонометрическое тождество: sin2y+cos2y=1 => cosy=+-  , cosy=
, cosy=  =
=  . По аналогии ищутся другие производные.
. По аналогии ищутся другие производные. =cos2y=(1+tg2y=
=cos2y=(1+tg2y=  =
=  . [arctg x]’=
. [arctg x]’=  *
* 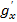 (без доказательства).
(без доказательства). => y’=y(ln f(x))’; логарифмическая производная применяется при вычислении производной функции вида y=
=> y’=y(ln f(x))’; логарифмическая производная применяется при вычислении производной функции вида y= 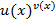
 при x<<1 можно заменить Δy на dy (Δy≈dy=f’(x0)Δx). y(x0 + Δx)-y(x0) ≈f’(x)dx, y(x0 + Δx) ≈ y(x0)+ f’(x0)dx
при x<<1 можно заменить Δy на dy (Δy≈dy=f’(x0)Δx). y(x0 + Δx)-y(x0) ≈f’(x)dx, y(x0 + Δx) ≈ y(x0)+ f’(x0)dx

 ,
, 
 =
=  =0,
=0,  , то существует и предельное значение
, то существует и предельное значение  =……
=……  . Данное правило используется для раскрытия неопределенностей вида
. Данное правило используется для раскрытия неопределенностей вида  ,
,  ,
,  .
. +
+  +…+
+…+  +
+  , остаточное слагаемое.
, остаточное слагаемое. *
*  .
.


