
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие товаропроизводителя. Метод изоквант- изокост.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выше установлено особое значение состояния равновесия и его условия для потребителя. Полезно ли вернуться теперь к понятию равновесия потребителя, пытаясь распространить его на товаропроизводителя? Да, именно так! Товаропроизводители и покупатели не просто посредники, обязанные считаться с устремлениями друг друга. Существенно и другое. Как говорят, они ведут себя рационально. Что это значит? Каждый из них стремится максимизировать для себя полезный результат с учетом наличных возможностей и ограничений. Потребитель стремится максимизировать общую полезность, принимая к сведению бюджетное ограничение. Товаропроизводитель (продуцент) выпускает продукцию не для себя. Он ее продает. При прочих равных условиях он заинтересован в максимально возможном выпуске продукции, если вся она находит покупателя. Чтобы организовать производство, приходится покупать на рынке факторы производства, нести определенные издержки. Рассматривая алгоритм принятия оптимального решения потребителем, мы ограничивались условием приобретения им двух благ. Поступим так и при толковании равновесия для товаропроизводителя. Положим, что он покупает на рынке два фактора производства. Находятся многочисленные варианты технических и технологических решений, обеспечивающие равный выпуск продукции при различной структуре задействованных факторов производства. Теоретически можно по-разному скомбинировать факторы производства и при этом понести равные общие издержки. Обозначим их ТС. Тогда: ТС = p1хF1 + p2xF2 Где p1 и p2 – цена за единицу производственных факторов (F1 и F2). Формально – математически получено уравнение прямой с двумя неизвестными, имеющее множество решений. Соответствующие линии на графике, точкам которых соответствуют равные общие издержки, получили название изокост (см. рис. 8.11). Точкам гипотенузы прямоугольного треугольника (изокосты) на графике соответствуют равные общие издержки. Последние собраны из затрат труда (L) и капитала (К). Каждой точке изокосты соответствует своя неповторимая структура издержек. Но для продуцента существенно именно то, что он несет равные суммарные издержки. Изменение цен на факторы производства, как и изменение расходных норм, приведет к тому или иному сдвигу изокосты на графике.
Графическая интерпретация издержек продуцента – изокоста – поразительно напоминает бюджетную линию потребителя, приобретающего два вида продукции (услуг). Это вовсе не случайно. Как продуцент, так и потребитель должны считаться с ограничением своих возможностей в части затрат.
Ранее показано, что продуцент стремится к максимальному объему производства и находит его на той или иной изокванте – кривой определенного выпуска продукции. Изокванта поразительно напоминает кривую безразличия потребителя, и это не случайно. Потребитель максимизирует общую полезность от приобретения двух благ. Продуцента интересует вариант максимального выпуска продукции или максимального чистого дохода (прибыли) при оптимальном сочетании двух расходуемых ресурсов. Потребитель так распределяет свой ограниченный бюджет, чтобы последняя денежная единица приносила равную предельную полезность от покупки любого блага. Продуцент так распределяет свои ограниченные ресурсы на покупку капитала и труда, чтобы уравнять предельный продукт каждого фактора производства в соответствии с его (фактора производства) ценой:
где МРк и МРL– предельный продукт капитала и труда соответственно; Рк и РL – цена единицы капитала и труда. Равновесие продуцента не обеспечено, если Неравенство свидетельствует о том, что процесс замещения труда капиталом (или наоборот) следует продолжить. Так, если
Теперь нас не удивит графическая интерпретация равновесия продуцента. Для нахождения равновесного состояния потребителя мы устанавливали точку касания одной из кривых безразличия с одной из бюджетных линий. Для нахождения равновесного состояния продуцента нам надлежит отыскать точку касания одной из изокост и изоквант (см. рис. 8.12).
Рис.8.12. Равновесие товаропроизводителя (продуцента)
На графике равновесие достигается в точке А и ни в какой другой.
Будем называть расход ресурсов, обеспечивающий максимальный выпуск при данных издержках и ценах ресурсов (например, капитала и труда), равновесным. Вводя понятие предельный нормы замещения для ресурса Х, устанавливаем, что она в общем случае равна отношению цен ресурсов: MPSx = px / py
Теперь не спешите расстаться с полученной формулой. Покажите в ходе самостоятельных рассуждений, что она правильна и экономически содержательна. Решим последние задачи по теме.
Задача 8.8.
Известно, что стоимость одного машино-часа аренды ЭВМ в 4 раза больше заработной платы преподавателя- экзаменатора. Расход машинного времени составляет 5 часов в день. Преподаватель принимает экзамен у 12 абитуриентов за 6 часов. Ставка заработной платы преподавателя, приведенная к одному часу, составляет 50 рублей. Сколько экзаменов должна принять ЭВМ, чтобы аренда была экономически эффективна?
Задача 8.9
Производственная функция Р = L 0,6K 0,4. При этом цена труда 50 ден. ед., а цена капитала 200ден.ед. Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия.
Решение задачи 8.8.
Это задача на равновесное состояние вуза. Предельный продукт (количество экзаменов) для ЭВМ (МРк), отнесенный к стоимости аренды ЭВМ (рк), должен быть больше предельного продукта преподавателя (МРL), отнесенного к его часовой зарплате:
ЭВМ должна проверить за 5 часов более 40 работ абитуриентов. Тогда аренда экономически эффективна.
Решение задачи 8.9.
Запишем условия равновесия фирмы:
Тогда АРL=
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.205.184 (0.012 с.) |


 =
=  ,
,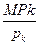 #
# 


 >
>  ;
;  >
> 
 >
>  ; MPk>
; MPk>  ; MPk>40
; MPk>40 =
=  =
=  =
= 
 = (
= (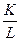 )0,4 = (
)0,4 = (


