Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
запасами з оптимальним рівнем запасівСодержание книги
Поиск на нашем сайте
запасами з оптимальним рівнем запасів 3.2.1. Модель з миттєвим витрачанням запасів Припустимо, що попит на продукцію, яка зберігається на складі на деякому інтервалі часу T, є випадкова величина X і заданий її закон розподілу. Якщо Х дискретна випадкова величина, яка приймає значення розподілу її є ряд розподілу Знаючи закон розподілу Дискретна модель Припустимо, що попит Позначимо через s – кількість одиниць товару, призначеного на склад. Можливі два взаємовиключні випадки: 1) 2) Така ситуація виникає, наприклад, якщо одночасно із виготовленням устаткування виготовляються також запасні частини до нього. Якщо вироблено надлишок запасних частин, то надлишки доводиться розпродавати із деякими збитками; якщо ж їх кількість менша необхідної, то доводиться закуповувати недостатню кількість по більш високій ціні (типовий приклад – запасні частини для імпортної автомобільної техніки). Розглянуті випадки зображені на рис. 3.2. Введемо позначення:
Y(t) Y(t)
t
Знаючи розподіл імовірностей попиту сподівання сумарних витрат, яке має вигляд
Отже, задача управління запасами у даній моделі полягає у знаходженні такого рівня запасу s, при якому математичне сподівання сумарних витрат Мінімум функції
де
– імовірність того, що рівень запасу не перевищує величини
– щільність збитків. Покажемо, як можна знайти мінімум функції
Оскільки
Таким чином,
де Тим же способом можна показати, що
Припустимо тепер, що
тобто
а співвідношення для
або
Звідкіля
Позначаючи Якщо виконуються нерівності (3.11), то звідси випливає, що Зауважимо, що якщо для деякого
тобто оптимум відповідає Аналогічно, якщо
тобто оптимум відповідає
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 3; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.2.68 (0.012 с.) |

 = 0, 1, 2,…, то законом
= 0, 1, 2,…, то законом , де
, де  – імовірність попиту k. Якщо Х неперервна величина, то її закон розподілу задається щільністю розподілу ймовірностей f(x). Імовірності
– імовірність попиту k. Якщо Х неперервна величина, то її закон розподілу задається щільністю розподілу ймовірностей f(x). Імовірності  ,
,  можна визначити математичне сподівання витрат, яке є економічною функцією для даної задачі. Задача управління запасами у даній моделі полягає у знаходженні такого рівня запасу
можна визначити математичне сподівання витрат, яке є економічною функцією для даної задачі. Задача управління запасами у даній моделі полягає у знаходженні такого рівня запасу  , при якому математичне сподівання сумарних витрат
, при якому математичне сподівання сумарних витрат  приймає мінімальне значення.
приймає мінімальне значення.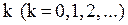 на інтервалі часу Т є випадковим і задано його закон розподілу
на інтервалі часу Т є випадковим і задано його закон розподілу 
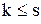 – запас перевищує попит і надлишок товару
– запас перевищує попит і надлишок товару  продається із збитками, рівними
продається із збитками, рівними 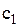 на кожну одиницю товару;
на кожну одиницю товару;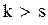 – є нестача товару і термінове придбання
– є нестача товару і термінове придбання 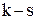 одиниць товару викликає необхідність у позаплановому поповненні, що веде до збитків
одиниць товару викликає необхідність у позаплановому поповненні, що веде до збитків 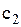 на одиницю товару.
на одиницю товару. витрати на поповнення одиниці продукції
витрати на поповнення одиниці продукції 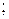
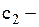 витрати на зберігання одиниці запасів;
витрати на зберігання одиниці запасів; витрати на одиницю дефіциту товару.
витрати на одиницю дефіциту товару.
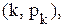 можна визначити математичне
можна визначити математичне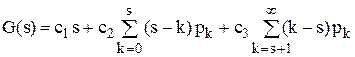 (3.10)
(3.10) набуде мінімального значення.
набуде мінімального значення.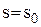 , яке задовольняє нерівностям
, яке задовольняє нерівностям , (3.11)
, (3.11) (3.12)
(3.12)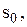 а
а
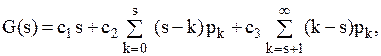
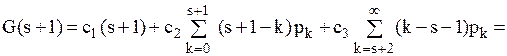

 .
.
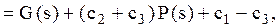
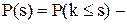 імовірність того, що попит менше або дорівнює
імовірність того, що попит менше або дорівнює 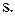
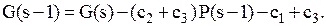
 задовольняє нерівності
задовольняє нерівності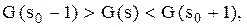
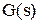 і
і 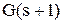 запишеться у вигляді
запишеться у вигляді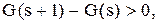 або
або 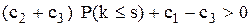 ,
, і
і 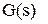 у вигляді
у вигляді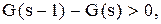


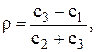 одержимо потрібне нам співвідношення (3.11).
одержимо потрібне нам співвідношення (3.11).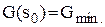
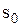 виконується співвідношення
виконується співвідношення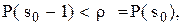 то
то 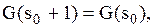 (3.13)
(3.13)
 то
то 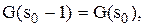 (3.14)
(3.14)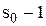 і
і