
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделі управління запасами в одному періодіСодержание книги
Поиск на нашем сайте
Неперервна модель У цьому випадку математичне сподівання втрат дорівнює
За формулою диференціювання інтеграла по параметру, знаходимо
де Прирівнюючи знайдену похідну до нуля, встановлюємо, що мінімум G(s) досягається при такому значенні
Покладемо
Дискретна модель Припустимо, що попит на товар на інтервалі часу Розглянемо наступний приклад. Станція технічного обслуговування автомобілів має склад деталей. Деякі дорогокоштуючі деталі завжди повинні знаходитись на складі і видаватись за вимогою клієнтів, оскільки не можна допустити затримки у ремонті автомобілів. Який запас s цих деталей повинна мати станція технічного обслуговування на складі, щоб мати мінімум витрат, пов’язаних із зберіганням і незадоволеним попитом (втрата клієнта або термінова закупівля деталей за завищеними цінами тощо). Позначимо через 1. При
2. При
Математичне сподівання сумарних витрат дорівнює
Мінімум функції G(s) досягається у точці
де
Функція Р(s) за означенням дорівнює Приклад 3.5. Деталі, які зберігаються на складі, витрачаються рівномірно протягом дня. Витрати на зберігання однієї деталі на складі складають
Визначимо необхідний оптимальний щоденний запас деталей на складі s, щоб можливі витрати на зберігання запасу і збитки від дефіциту були б мінімальні. Алгоритм реалізації моделі v задаємо величини v визначаємо щільність збитків v записуємо вирази для цільової функції G(s) і функції L(s); v визначаємо оптимальне значення обсягу запасу v визначаємо мінімальне значення цільової функції Алгоритм у Mathcad
Визначення значення
Коментар. У даній моделі оптимальна політика управління запасами полягає у створенні щоденного запасу деталей на складі у кількості Приклад 3.6. Розглянемо попередню модель при витратах Визначимо оптимальний рівень запасів Обчислення проводимо за наступним алгоритмом: v задаємо значення показників витрат v задаємо параметр експоненціального розподілу v записуємо вирази для функцій Алгоритм у Mathcad
Розв’язання рівняння
Коментар. Політика управління запасами у даній моделі полягає у створенні оптимального запасу у Моделі систем управління запасами в одному періоді (одноетапні моделі) відображають ситуацію, коли для задоволення попиту протягом певного періоду часу продукція замовляється тільки один раз. На практиці такі задачі виникають при постачанні запасних частин або продуктів, що швидко псуються, товарів, які швидко виходять із моди, а також сезонних товарів. Наприклад, марка автомобіля застаріває і, отже, замовлення на деталі не поновлюються. Одноетапні моделі досліджуються при різних припущеннях, у тому числі при миттєвому і рівномірному попиті з урахуванням і без урахування витрат на оформлення замовлень. Припускається, що поповнення запасу здійснюється миттєво на початку періоду. Модель визначає оптимальний рівень запасу при умові мінімізації очікуваних витрат на управління запасами, які включають витрати на розміщення замовлення (витрати на закупівлю або виробництво), витрати на зберігання і втрати від дефіциту. У зв’язку із імовірнісним характером попиту витрати на закупівлю продукції, хоча і є постійними, є суттєвим фактором у загальній функції витрат. При відомому оптимальному значенні q = q0 оптимальне управління запасами полягає у подачі замовленняобсягом
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 4; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.245.44 (0.012 с.) |

 . (3.18)
. (3.18)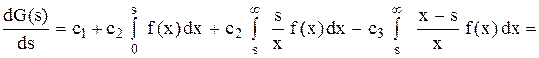
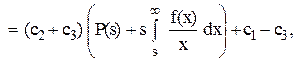
 .
.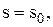 при якому
при якому (3.19)
(3.19)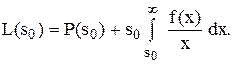 Тоді умова (3.12) запишеться у вигляді
Тоді умова (3.12) запишеться у вигляді (3.20)
(3.20) є випадковим і заданий рядом розподілу ймовірностей
є випадковим і заданий рядом розподілу ймовірностей  , де
, де 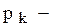 імовірність попиту на k одиниць товару. Витрати на зберігання одиниці товару в одиницю часу дорівнюють
імовірність попиту на k одиниць товару. Витрати на зберігання одиниці товару в одиницю часу дорівнюють 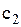 , нестача одиниці товару призводить до збитків у розмірі
, нестача одиниці товару призводить до збитків у розмірі 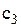 .
. , інтервал
, інтервал  і
і 
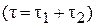 , де
, де 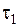 – час, коли запас є,
– час, коли запас є,  – коли запас відсутній. Припускаючи, що зміна запасу може відбуватись лінійно, будемо мати два випадки:
– коли запас відсутній. Припускаючи, що зміна запасу може відбуватись лінійно, будемо мати два випадки: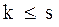 середній запас на проміжку часу
середній запас на проміжку часу 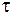 дорівнює
дорівнює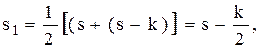
 середній запас на проміжку
середній запас на проміжку  і середня нестача запасу на проміжку
і середня нестача запасу на проміжку 

 (3.21)
(3.21)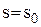 , для якої виконуються нерівності
, для якої виконуються нерівності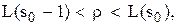 (3.22)
(3.22) ,
, 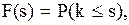
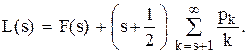
 Як легко помітити,
Як легко помітити, 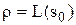 означає, що
означає, що  і
і  відповідають оптимуму, а
відповідають оптимуму, а 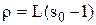 означає, що оптимуму відповідають
означає, що оптимуму відповідають  . Порівняння
. Порівняння  і L(s) зразу дає
і L(s) зразу дає 
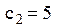 грн., а штраф за дефіцит деталі обходиться у
грн., а штраф за дефіцит деталі обходиться у 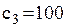 грн. для спрощення обчислень покладемо
грн. для спрощення обчислень покладемо  Розподіл імовірностей попиту на деталі
Розподіл імовірностей попиту на деталі 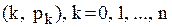 заданий у таблиці
заданий у таблиці
 і розподіл імовірностей попиту
і розподіл імовірностей попиту 
 використовуючи співвідношення (3.10). Для цього використовується оператор Mathcad
використовуючи співвідношення (3.10). Для цього використовується оператор Mathcad  який дає значення
який дає значення  , якщо задана умова виконується і 0 у протилежному випадку;
, якщо задана умова виконується і 0 у протилежному випадку;

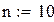
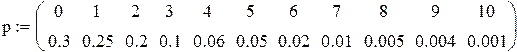
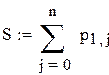
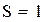

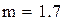
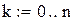
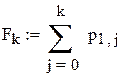


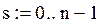

 яке дає мінімум функції G(s)
яке дає мінімум функції G(s)

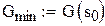
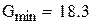
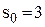 деталі при середньому значенні попиту
деталі при середньому значенні попиту  деталі. Мінімальні втрати дорівнюють
деталі. Мінімальні втрати дорівнюють 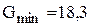 грн. ▲
грн. ▲ , але попит розподілений за експоненціальним законом із щільністю розподілу ймовірностей
, але попит розподілений за експоненціальним законом із щільністю розподілу ймовірностей 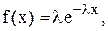 де
де  параметр розподілу, який дорівнює
параметр розподілу, який дорівнює 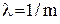 , m – середнє значення попиту. Для заданого розподілу ймовірностей середній попит m = 1,7, отже
, m – середнє значення попиту. Для заданого розподілу ймовірностей середній попит m = 1,7, отже 
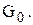
 і визначаємо величину
і визначаємо величину  ;
; і записуємо відповідні вирази для щільності розподілу ймовірностей
і записуємо відповідні вирази для щільності розподілу ймовірностей  і функції розподілу
і функції розподілу 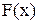 ;
; і рівняння
і рівняння 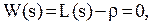 із якого визначаємо значення
із якого визначаємо значення 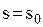 , яке є точкою мінімуму функції
, яке є точкою мінімуму функції 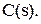
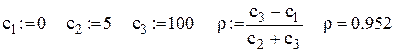

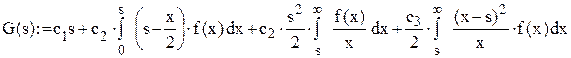


 , визначення точки екстремуму
, визначення точки екстремуму 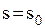 і мінімуму функції
і мінімуму функції 
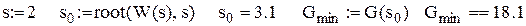
 одиниць товару при середньому попиті
одиниць товару при середньому попиті 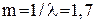 одиниць. Мінімальні витрати дорівнюватимуть
одиниць. Мінімальні витрати дорівнюватимуть  грн. ▲
грн. ▲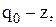 якщо
якщо 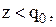 у протилежному випадку замовлення не подається.
у протилежному випадку замовлення не подається.


