
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделі систем управління запасами з двомаСодержание книги
Поиск на нашем сайте
рівнем запасів Розглянемо спочатку точні рівняння для
де Обчислимо середнє число замовлень
Таким чином, середнє число замовлень, врахованих за рік, і середня інтегральна нестача за рік дорівнюють
Враховуючи одержані вирази, середні річні витрати дорівнюватимуть
Звідси
Найменше
Відмітимо, що (5.37) справедливе для всіх Оптимальні значення Виведемо тепер точні рівняння для Безпосередньо із (5.25) випливає, що
Аналогічно із (5.28) і (5.29) маємо
Таким чином, сумарні середні річні витрати дорівнюють
де
де
Алгоритм реалізації моделі v задаємо вхідні дані моделі v записуємо функцію щільності ймовірності нормованого нормального розподілу v визначаємо середню кількість врахованих за рік замовлень v визначаємо середню інтегральну нестачу товарів за рік v визначаємо функцію середніх річних витрат Для знаходження оптимальних значень v задаємо діапазони можливих значень параметрів v представляємо масив значень функції Мінімальне значення функції v визначаємо гарантійний запас Приклад 5.4. Розглянемо алгоритм реалізації Визначимо оптимальну політику управління запасами у даній системі, використовуючи Алгоритм реалізації даної моделі аналогічний алгоритму попередньої моделі. Відповідні параметри нормального розподілу попиту дорівнюють Алгоритм у Mathcad
Перетворення масиву значень функції
Фрагмент матриці
Мінімальне значення середніх річних витрат
Індекси
Функціональні характеристики: Ø Середня кількість врахованих замовлень за рік Ø Середня інтегральна нестача товарів за рік Ø Середній обсяг запасу у системі за рік
Ø Середній гарантійний запас
Коментар. Оптимальна стратегія управління запасами за даною моделлю характеризується такими параметрами: фіктивний рівень запасів в момент перевірки Ці результати показують, що розглянута у даному прикладі рівнями запасів У цих моделях використовується Щоб одержати у явній формі вираз для середніх річних витрат приймемо такі припущення: Ø попит є стаціонарним випадковим процесом; Ø попит у різні періоди часу є незалежним; Ø час поставки постійний. Раніш ніж зосередити увагу на випадку пуассонівського розподілу попиту, обчислимо для довільного розподілу попиту Випадковий процес переходів із стану у стан може розглядатись як марковський ланцюг із скінченим числом станів. Виведемо рівняння, яким повинні задовольняти ймовірності Рівень запасів у системі зразу ж по закінченню перевірки може прийняти одне із
Таким чином
Стаціонарні ймовірності
Є очевидним, що даний розподіл не є рівномірним, як це було раніше, оскільки стану Знайдемо ймовірності станів Обмежуючись випадком, коли попит породжується пуассонівським потоком вимог одиничної величини, одержимо явний вираз для сумарних середніх річних витрат як функцій від Нехай Припустимо, що замовлення на поповнення подається в момент
У циклі завжди є щонайменше один період, а на першому періоді сумарні витрати складають
якщо, за означенням, покласти
Визначивши середні витрати на зберігання запасів і облік замовлень за цикл, ми повинні тепер знайти середнє число циклів у рік, тобто величину, обернену до середньої тривалості циклу. Тривалість періоду дорівнює Обчислимо середнє число періодів у циклі. Цикл в точності дорівнює одному періоду, якщо попит у першому періоді циклу перевищує величину
Розглянемо тепер імовірність того, що цикл складається в точності із
Отже, середнє число періодів у циклі складає
Якщо скористатись введеним вище означенням
Тепер можна записати вираз для сумарних річних витрат. Якщо, як і звичайно,
Якщо відомий розподіл попиту, то можна у явній формі виписати вирази для Зауважимо, що величина
представляє собою відповідні витрати зберігання запасів і обліку замовлень за період. Але, за означенням
Звідси випливає, що
Можна довести, що це дійсно так [8], і Звернемось тепер до випадку, коли обсяг попиту розподілений за законом Пуассона. Тоді
Тепер можна виписати явний вираз для
Аналогічно середня інтегральна нестача за період від
Нарешті, середня кількість одиниць запасу на інтервалі від
Підсумовуючи одержані складові витрат, одержимо середні витрати на зберігання і облік замовлень на інтервалі від
З урахуванням (5.49) середні загальні річні витрати, які були визначені у (5.44), тепер будуть визначатись таким виразом:
Оптимізація даної моделі за критерієм, визначеним виразом (5.55), класичними методами є складною задачею, оскільки функція Алгоритм реалізації моделі v задаємо вхідні дані моделі v записуємо вираз для розподілу Пуассона v визначаємо складові функції витрат: v визначаємо функцію середніх річних витрат v задаємо діапазони можливих значень параметрів v для кожного v мінімальне значення функції v визначаємо індекси Приклад 5.5. Розглянемо систему військового постачання, у якій зберігається деякий дорогокоштуючий матеріал. Попит на нього можна вважати розподіленим за законом Пуассона із середньою інтенсивністю 100 одиниць у рік. Вартість подачі замовлення на поповнення запасу складає 4 тис. грн., вартість перевірки рівня запасів – 2 тис. грн. Ціна одиниці дорівнює 10 тис. грн. незалежно від розміру замовлення. Усі замовлення, які надходять у систему, коли в ній нема запасів, реєструються, і втрати від кожного такого врахованого замовлення оцінюється у 20 тис. грн. незалежно від часу, який пройшов з моменту реєстрації замовлення. Втрати, пов’язані із часом дефіциту матеріалу, обходяться у 2 тис. грн. Час поставки є випадковою величиною із середнім 0,1 року. Коефіцієнт витрат утримання запасів дорівнює 0,2. Застосовуючи Алгоритм у Mathcad
Перетворення масиву значень функції
Фрагмент матриці Z
Мінімальне значення середніх річних витрат
Коментар. Оптимальна стратегія управління запасами у даній системі має такі параметри: оптимальний фіктивний рівень запасів (обсяг наявних запасів плюс обсяг ще невиконаних замовлень) Контрольні запитання 1. Дати характеристику системи управління запасами з періодичними перевірками. Які стратегії функціонування застосовуються у даній моделі. 2. Чи вірно, що у системі управління запасами з періодичними перевірками використовується стратегія функціонування, згідно якої замовлення на поповнення запасів подається в момент перевірки тільки у тому випадку, якщо попит за попередній період функціонування перевищив рівень наявних запасів. 3. Яка стратегія управління запасами називається правилом постійного рівня (або 4. Чи вірно, що у системі з періодичними перевірками в момент перевірки замовляється партія товарів, яка доводить фіктивний рівень запасів до деякого значення 5. Дати характеристику системи управління запасами, у якій використовується 6. У яких системах управління запасами використовується стратегія, при якій замовлення на поповнення запасів подаються, коли в момент перевірки фіктивний рівень запасів у системі виявляється меншим або рівним величині 7. Дати характеристику 8. У чому полягає мета дослідження систем управління запасами з періодичними перевірками. Які параметри цієї системи є визначальними. Чи може бути період перевірки Т довільним. 9. Які витрати потрібно включати у функцію загальних витрат у системах з періодичними перевірками. Чи потрібно включати вартість перевірки стану запасів, витрати, пов’язані із подачею замовлень на поповнення запасів, витрати зберігання запасів і витрати, пов’язані з обліком незадовільнених замовлень. 10. Чому у системі управління запасами з періодичними перевірками середні річні витрати на зберігання запасів складають 11. Чи вірно, що середня кількість 12. У системі із втратою замовлень витрати зберігання запасів визначаються без урахування кількості втрачених замовлень. 13. Чи залежить подача замовлення на поповнення запасу у Задачі 5.1. На одному із складів торгівельної фірми секції перевіряються раз у квартал. Для кожної секції використовується Визначити оптимальний рівень запасів Параметри моделі:
5.2. Система управління запасами, у якій використовується Визначити оптимальну політику управління запасами у даній системі, використовуючи Параметри моделі:
5.3. Розглянемо Визначити оптимальну політику управління запасами у даній системі, використовуючи Відповідні параметри нормального розподілу попиту дорівнюють Параметри моделі:
5.4. Розглянути алгоритм реалізації Визначити оптимальну політику управління запасами у даній системі, використовуючи Параметри моделі:
5.5. Розглянемо систему постачання, у якій зберігається деякий дорогокоштуючий матеріал. Попит на нього можна вважати розподіленим за законом Пуассона із середньою інтенсивністю Застосовуючи Параметри моделі:
5.6. Стан кожного товару, який зберігається на складі, перевіряється один раз у квартал. Використовується Треба визначити оптимальні параметри роботи складу: Ø оптимальне значення фіктивного рівня запасів Ø оптимальний період перевірки і оптимальний рівень запасів Ø найменші річні витрати, які можна досягти, якщо використовувати оптимальне значення періоду перевірки. Параметри моделі:
5.7. Побудуйте дискретний аналог моделі управління запасами із підрозділу 5.2 для випадку пуассонівського процесу попиту. Розгляньте випадок постійного і випадкового часу поставок. Яка нерівність використовується при визначенні фіктивного рівня запасів 5.8. На складі торгівельної фірми зберігаються товари , стан яких перевіряється один раз у три місяці. Використовується Треба визначити оптимальні параметри роботи складу: Ø оптимальне значення фіктивного рівня запасів Ø гарантійний запас; Ø витрати у наслідок випадкового характеру попиту. Параметри моделі: 5.9. В універсальному магазині раз у тиждень перевіряється наявність в асортименті білих чоловічих сорочок. Використовується Визначити оптимальні параметри прийнятої стратегії управління запасами: Ø оптимальне значення фіктивного рівня запасів Ø гарантійний запас; Ø витрати у наслідок випадкового характеру попиту. Параметри моделі: 5.10. Також, як і у випадку 5.11. Розгляньте питання, пов’язані із нелінійністю витрат, які виникають у наслідок дефіциту у системах із періодичною перевіркою. Нехай 5.12. У системі військового постачання, у якій зберігається деякий дефіцитний матеріал, запас якого перевіряється один раз у тиждень. Використовується Визначити оптимальні параметри прийнятої стратегії управління запасами: Ø оптимальні значення фіктивного рівня запасів в момент поставки Ø мінімальні річні витрати у наслідок випадкового характеру попиту. Параметри моделі:
Література 1. Бродецкий Г.Л. Управление запасами: учебное пособие. – М.: Эксмо, 2008. 2. Букан Дж., Кенигсберг Э. Научное управление запасами. – М.: Наука. 1967. 3. Голенко Д. И., Дакелин А.И., Лившиц С.Е. Моделирование в технико-економических системах. Изд. Ленинградского ун-та, 1975. – 197 с. 4. Дьяконов В. Mathcad 8/2000: спец. справочник – СПб: “Питер”, 2000. 5. Зайченко Ю.П. Дослідження операцій: Підручник. – 4-те вид., перероблене і доповнене. – К., 2001. – 688 с. 6. Кофман А. Методы и модели исследования операций. – М.: Высш. школа. Изд. “Мир”. 1966. 7. Кремер Н. Ш. и др. Исследование операций в экономике. – М.: – ЮНИТИ. 2001. – 407 с. 8. Математическое моделирование. Под ред. Дж. Эндрюса и Мак-Лоуна. Изд. “Мир”. 1979. – 248 с. 9. Рыжиков Ю.И. Управление запасами. – М.: Наука. 1969. –344 с. 10. Таха Х., Хэмди А. Введение в исследование операций. 6-е издание. – М.: Издательский дом “Вильямс”. 2001. – 912 с. 11. Хедли Дж., Уайтин Т. Анализ систем управления запасами. – М.: Наука. 1969. Предметний покажчик В Вартість поставки 9 Види витрат 9 середні річні 18, 142, 149, 173 залежні від часу 110 зберігання запасів 9 лінійні 23, 25, 36 поповнення запасу 8 Втрачена вартість (штрафи) 10 Г, І Гарантійний запас 8, 64 Імовірність ризику дефіциту 66 Інтенсивність 13 К Класифікація моделей управління запасами 11 Критерії ефективності 10 максимізації середнього прибутку 102 середніх витрат 22 М Модель системи управління запасами динамічна 13 детермінована 13, 16,49 статична 13 стохастична 13, 64,28 без дефіциту 16 в одному періоді 64, 89 з дефіцитом 27 з періодичним поповненням запасів типу з груповим поповненням запасів 191 з критичним рівнем з миттєвим витрачанням запасів 76 з рівномірним витрачанням запасів 85 трипараметрична з витратами, пропорційними обсягу поставки 23 з втратами незадовільнених замовлень 41, 130, 184 з обмеженою інтенсивністю поповнення запасів 44
з періодичними поповненням 128, 181 наближена (q, r)- модель з обліком невиконаних замовлень 128, 182 з втратами невиконаних замовлень 134 з різними рівнями цін 53 оперативного управління 128 періодична з граничним верхнім рівнем при q=1 166 при випадковому часі поставок 170 система двох рівнів точна з втратами замовлень 141, 161 частинний випадок 149 з втратами замовлень 41, 134, 141 О, П Обсяг замовлення 13 Оптові знижки цін 53 Період виконання замовлення 66 Попит 7, 90 Р Рівень запасів середній 18, 147, 148 Рівень обслуговування 70 Рівень ризику дефіциту 64 Розмір партії економічний 18 С Середня кількість врахованих замовлень 142, 146 втрачених замовлень 142, 146 нестач запасу 142, 147 Середній річний прибуток 102,, 116 Стратегія управління запасами 11 Страховий (гарантійний) запас 8 Структура складської системи 9 Т, Ф Точка замовлення 12, 20 Формула Уілсона 18 Ц, Ч, Ш, Щ Цикл 66 Час поставки 8 Число партій постачання 17 Штраф за дефіцит 10 Щільність збитків 30
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.23 (0.012 с.) |

 -моделі при постійному часі поставок і попиті, розподіленому за законом Пуассона. Ці рівняння можна одержати із рівнянь підрозділу 5.2.1, якщо покласти в них
-моделі при постійному часі поставок і попиті, розподіленому за законом Пуассона. Ці рівняння можна одержати із рівнянь підрозділу 5.2.1, якщо покласти в них  Насамперед із (5.13) видно, що імовірність
Насамперед із (5.13) видно, що імовірність 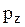 подачі замовлення у довільний момент часу дорівнює
подачі замовлення у довільний момент часу дорівнює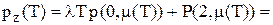 (5.33)
(5.33)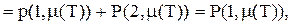

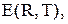 врахованих за рік, і середню інтегральну нестачу за рік
врахованих за рік, і середню інтегральну нестачу за рік 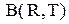 . Їх легко одержати, поклавши
. Їх легко одержати, поклавши 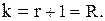 Отже будемо мати
Отже будемо мати  .
.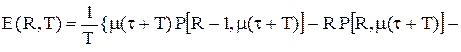 (5.34)
(5.34)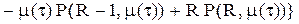 .
. (5.35)
(5.35)
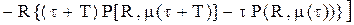
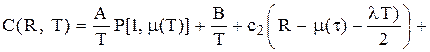 (5.36)
(5.36)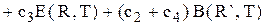 .
. (5.37)
(5.37)



 =
=

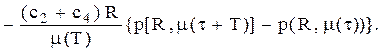
 , яке мінімізує функцію
, яке мінімізує функцію  є найбільше
є найбільше  для якого
для якого  Для знаходження
Для знаходження 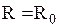 , яке задовольняє вказаній умові, можна застосувати чисельні методи. Втім, у багатьох випадках можна знехтувати доданками, які залежать від
, яке задовольняє вказаній умові, можна застосувати чисельні методи. Втім, у багатьох випадках можна знехтувати доданками, які залежать від 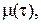 у порівнянні із членами, які залежать від
у порівнянні із членами, які залежать від  У результаті цього вираз для
У результаті цього вираз для  спрощується і має вигляд
спрощується і має вигляд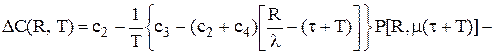 (5.38)
(5.38)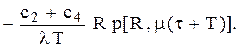
 тоді як (5.38) виконується тільки для досить великих Т.
тоді як (5.38) виконується тільки для досить великих Т.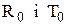 простіше всього визначати, застосовуючи алгоритм перетворення масиву значень
простіше всього визначати, застосовуючи алгоритм перетворення масиву значень 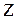 і визначаючи її мінімальний елемент
і визначаючи її мінімальний елемент  та його індекси, за якими остаточно знаходяться
та його індекси, за якими остаточно знаходяться  у матрицю
у матрицю 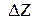 і знаходячи індекси першого її елемента, який є додатним.
і знаходячи індекси першого її елемента, який є додатним.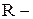 неперервна величина, а обсяг попиту за довільний проміжок часу розподілений за нормальним законом із середнім
неперервна величина, а обсяг попиту за довільний проміжок часу розподілений за нормальним законом із середнім  і дисперсією
і дисперсією 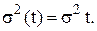 Для того, щоб скористатись результатами попереднього розділу, треба у виведених там рівняннях покласти
Для того, щоб скористатись результатами попереднього розділу, треба у виведених там рівняннях покласти  і перейти до границі при
і перейти до границі при 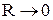 (у дискретному випадку ми покладали
(у дискретному випадку ми покладали  Очевидно, що у неперервному випадку
Очевидно, що у неперервному випадку 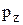 повинна дорівнювати 1, оскільки ймовірність того, що сумарний попит за довільний проміжок часу відмінний від нуля, дорівнює 1. До такого ж висновку приводить співвідношення (5.25), якщо покласти у ньому
повинна дорівнювати 1, оскільки ймовірність того, що сумарний попит за довільний проміжок часу відмінний від нуля, дорівнює 1. До такого ж висновку приводить співвідношення (5.25), якщо покласти у ньому 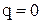 і припустити, що у області від’ємних значень аргументу щільність імовірності досить близька до нуля.
і припустити, що у області від’ємних значень аргументу щільність імовірності досить близька до нуля.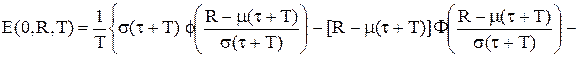
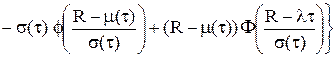

 (5.40)
(5.40) (5.41)
(5.41) При фіксованому Т оптимальне значення
При фіксованому Т оптимальне значення 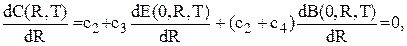 (5.42)
(5.42) ,
, 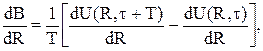

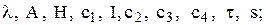
 і його додаткову функцію розподілу
і його додаткову функцію розподілу 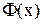 ;
;
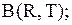
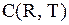 .
. застосуємо алгоритми дискретної оптимізації (перебірний алгоритм):
застосуємо алгоритми дискретної оптимізації (перебірний алгоритм):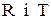 відповідно
відповідно  і
і 
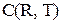 у вигляді матриці
у вигляді матриці  де
де 
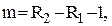


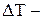 крок зміни параметра Т,
крок зміни параметра Т, 
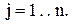
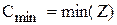 матриці
матриці  . Далі визначаємо індекси
. Далі визначаємо індекси 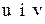 мінімального елемента матриці
мінімального елемента матриці 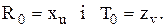
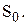
 .
.





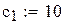

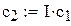





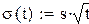
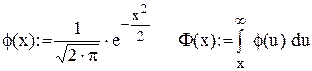

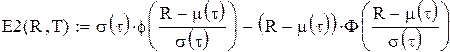

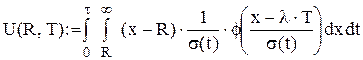

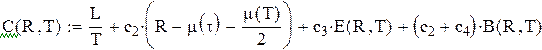
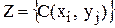 і визначення оптимальних значень
і визначення оптимальних значень 
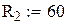

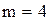




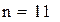
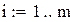

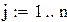




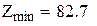
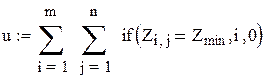

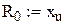

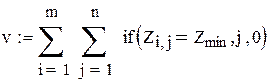

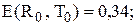
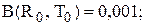

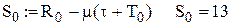
 одиниць, період перевірки
одиниць, період перевірки  року (2,4 місяця). Середні мінімальні витрати на функціонування системи складуть
року (2,4 місяця). Середні мінімальні витрати на функціонування системи складуть 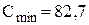 грош. од.
грош. од.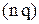 -стратегія, розглянута у попередньому прикладі. Це підтверджує той факт, що коли вартість перевірки системи менша вартості подачі замовлення (
-стратегія, розглянута у попередньому прикладі. Це підтверджує той факт, що коли вартість перевірки системи менша вартості подачі замовлення ( 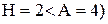 , перевагу має
, перевагу має  -стратегія управління. При використанні цієї стратегії у моменти перевірок замовляється партія, яка поповнює рівень запасів (для системи з обліком замовлень) або сумарний обсяг наявних запасів і ще невиконаних замовлень на поповнення (для системи із втратою замовлень) до рівня
-стратегія управління. При використанні цієї стратегії у моменти перевірок замовляється партія, яка поповнює рівень запасів (для системи з обліком замовлень) або сумарний обсяг наявних запасів і ще невиконаних замовлень на поповнення (для системи із втратою замовлень) до рівня  Для прийнятих тут функцій витрат при випадковому попиті
Для прийнятих тут функцій витрат при випадковому попиті 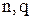 -стратегією або
-стратегією або  -стратегія, попит розподілений за законом Пуассона і час поставки постійний. Обчислимо середні річні витрати, підрахувавши середні витрати за один цикл роботи системи і помноживши цей результат на загальну кількість циклів.
-стратегія, попит розподілений за законом Пуассона і час поставки постійний. Обчислимо середні річні витрати, підрахувавши середні витрати за один цикл роботи системи і помноживши цей результат на загальну кількість циклів. стаціонарні ймовірності того
стаціонарні ймовірності того 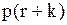 , що до моменту закінчення перевірки рівень запасів у системі дорівнює
, що до моменту закінчення перевірки рівень запасів у системі дорівнює  Якщо нам буде відомий розподіл імовірностей
Якщо нам буде відомий розподіл імовірностей 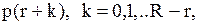 то ми зможемо обчислити середні річні витрати точно також, як це було зроблено для
то ми зможемо обчислити середні річні витрати точно також, як це було зроблено для  -моделі.
-моделі.
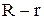 значень
значень  Для того, щоб обчислити перехідні ймовірності
Для того, щоб обчислити перехідні ймовірності  припустимо, що до закінчення чергової перевірки рівень запасів у системі дорівнює
припустимо, що до закінчення чергової перевірки рівень запасів у системі дорівнює 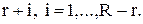 Необхідно обчислити ймовірність того, що до кінця наступної перевірки рівень запасів у системі складе
Необхідно обчислити ймовірність того, що до кінця наступної перевірки рівень запасів у системі складе 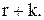 Якщо
Якщо  то ця ймовірність дорівнює нулю, оскільки такі переходи неможливі. Якщо
то ця ймовірність дорівнює нулю, оскільки такі переходи неможливі. Якщо 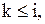 то
то  . Коли
. Коли  і
і  імовірність переходу буде дорівнювати
імовірність переходу буде дорівнювати 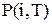 , де
, де  функція розподілу, пов’язана із
функція розподілу, пов’язана із  Коли
Коли 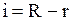 і
і 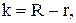 тобто у випадку, якщо замовлення на склад не надходили, то цьому випадку відповідає ймовірність
тобто у випадку, якщо замовлення на склад не надходили, то цьому випадку відповідає ймовірність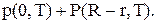
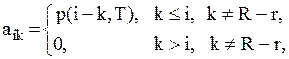

 .
.
 (5.43)
(5.43) у явному вигляді. Обчисливши середні витрати на інтервалі або у циклі між моментами послідовної подачі двох замовлень на поповнення і помноживши одержаний результат на середню кількість таких інтервалів у рік, спочатку буде виведений точний вираз для сумарних середніх річних витрат. Із цього виразу будуть одержані ймовірності
у явному вигляді. Обчисливши середні витрати на інтервалі або у циклі між моментами послідовної подачі двох замовлень на поповнення і помноживши одержаний результат на середню кількість таких інтервалів у рік, спочатку буде виведений точний вираз для сумарних середніх річних витрат. Із цього виразу будуть одержані ймовірності  .
.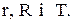 Із цього виразу ми одержимо загальний розв’язок рівнянь (5.43).
Із цього виразу ми одержимо загальний розв’язок рівнянь (5.43). є ймовірність того, що попит за період складе
є ймовірність того, що попит за період складе 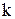 одиниць. Тоді у наслідок припущення про незалежність попиту у різні періоди роботи системи ймовірність того, що попит за
одиниць. Тоді у наслідок припущення про незалежність попиту у різні періоди роботи системи ймовірність того, що попит за  періодів складе
періодів складе 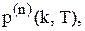 де
де  – n-кратна композиція
– n-кратна композиція  Нехай
Нехай 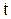 означає момент перевірки, і нехай зразу ж після прийняття рішення про необхідність поповнення складських запасів фіктивний рівень запасів у системі дорівнює
означає момент перевірки, і нехай зразу ж після прийняття рішення про необхідність поповнення складських запасів фіктивний рівень запасів у системі дорівнює  – сума середніх витрат по зберіганню і обліку замовлень на інтервалі від
– сума середніх витрат по зберіганню і обліку замовлень на інтервалі від 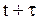 до
до  де
де 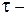 час поставки.
час поставки. Починаючи з цього моменту до
Починаючи з цього моменту до  включно, не подається більше жодного замовлення, а фіктивний рівень запасів до моменту
включно, не подається більше жодного замовлення, а фіктивний рівень запасів до моменту  дорівнює
дорівнює  за час
за час  на склад замовлено в точності
на склад замовлено в точності 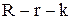 одиниць запасу. Імовірність цієї події дорівнює
одиниць запасу. Імовірність цієї події дорівнює  Середні витрати зберігання і середня вартість обліку замовлень на інтервалі від
Середні витрати зберігання і середня вартість обліку замовлень на інтервалі від 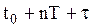 до
до 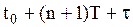 складе
складе 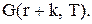 Далі, починаючи з
Далі, починаючи з  -му періоді витрати зберігання і витрати на враховані замовлення складуть
-му періоді витрати зберігання і витрати на враховані замовлення складуть 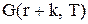 при умові, що до початку
при умові, що до початку 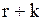 одиниць. Імовірність того, що цикл складається більше ніж із
одиниць. Імовірність того, що цикл складається більше ніж із  періодів, а рівень запасів до початку
періодів, а рівень запасів до початку 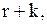 дорівнює
дорівнює 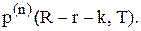 Таким чином, в середньому витрати зберігання і витрати на облік замовлень у
Таким чином, в середньому витрати зберігання і витрати на облік замовлень у 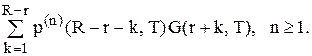
 грош. одиниць, оскільки зразу ж після подачі замовлення фіктивний рівень запасів у системі дорівнює
грош. одиниць, оскільки зразу ж після подачі замовлення фіктивний рівень запасів у системі дорівнює 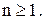 Таким чином, ці середні витрати дорівнюють
Таким чином, ці середні витрати дорівнюють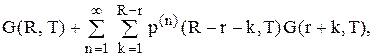

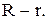 Імовірність цієї події дорівнює
Імовірність цієї події дорівнює 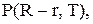 де
де  дорівнює одиниці мінус функція розподілу, яка одержується підсумовуванням імовірностей
дорівнює одиниці мінус функція розподілу, яка одержується підсумовуванням імовірностей 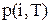 від 0 до
від 0 до  тобто
тобто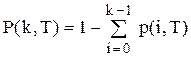 або
або 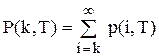 .
. Якщо у перших
Якщо у перших  періодах після подачі чергового замовлення із складу було замовлено
періодах після подачі чергового замовлення із складу було замовлено  то цикл буде триватись в точності
то цикл буде триватись в точності 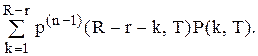

 то це можна записати у вигляді
то це можна записати у вигляді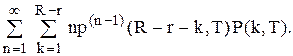
 вартість подачі замовлення і
вартість подачі замовлення і 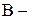 вартість перевірки, то сумарні річні витрати дорівнюють
вартість перевірки, то сумарні річні витрати дорівнюють (5.44)
(5.44) Раніш ніж зробити це для випадку, коли попит породжується пуассонівським потоком вимог одиничної величини, знайдемо із (5.44) стаціонарні ймовірності
Раніш ніж зробити це для випадку, коли попит породжується пуассонівським потоком вимог одиничної величини, знайдемо із (5.44) стаціонарні ймовірності 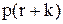 , знаходячи тим самим розв’язок системи (5.43).
, знаходячи тим самим розв’язок системи (5.43).
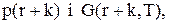 середні витрати за період дорівнюють
середні витрати за період дорівнюють
 (5.45)
(5.45) які визначаються за формулою (5.45), задовольняють системі рівнянь (5.43).
які визначаються за формулою (5.45), задовольняють системі рівнянь (5.43).
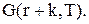 Це вже було зроблено для
Це вже було зроблено для 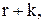 то середня кількість замовлень, врахованих на інтервалі від
то середня кількість замовлень, врахованих на інтервалі від 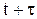 до
до 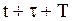 дорівнює
дорівнює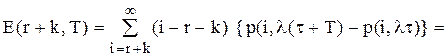 (5.46)
(5.46)
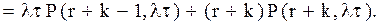
 складає
складає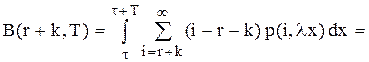 (5.47)
(5.47)
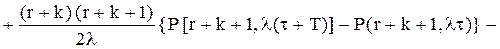
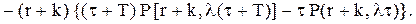
 (5.48)
(5.48)
 (5.49)
(5.49)
 (5.50)
(5.50) залежить від параметрів
залежить від параметрів 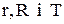 досить складним чином. Тому, як і у попередніх моделях, для чисельної реалізації даної моделі застосуємо алгоритм дискретної оптимізації. Розглянемо алгоритм, у якому попит розподілений за законом Пуассона.
досить складним чином. Тому, як і у попередніх моделях, для чисельної реалізації даної моделі застосуємо алгоритм дискретної оптимізації. Розглянемо алгоритм, у якому попит розподілений за законом Пуассона.
 і його додаткову функцію розподілу
і його додаткову функцію розподілу 


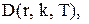
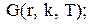
 ;
; відповідно
відповідно  послідовність значень параметра
послідовність значень параметра 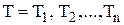 ;
;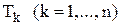 представляємо значення функції
представляємо значення функції 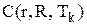 у вигляді масиву (матриці)
у вигляді масиву (матриці) 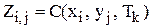 де
де 

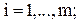


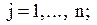
 знаходимо як мінімальний елемент
знаходимо як мінімальний елемент 
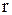 і період перевірки рівня запасів
і період перевірки рівня запасів 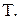


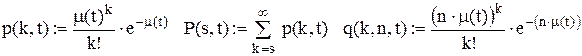
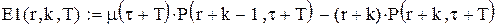

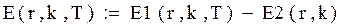
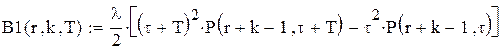
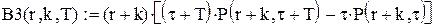

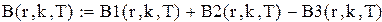
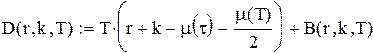
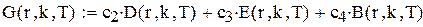
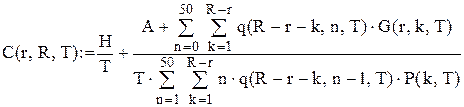
 у матрицю
у матрицю 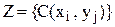 при
при  і визначення оптимальних значень
і визначення оптимальних значень 




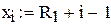
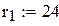
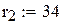
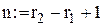
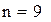



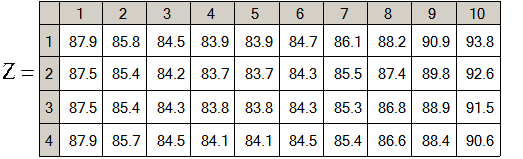
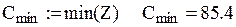


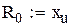
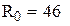
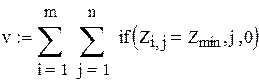

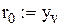
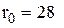
 оптимальний рівень подачі замовлення
оптимальний рівень подачі замовлення  оптимальний період перевірки стану запасів
оптимальний період перевірки стану запасів  (1,6 місяця). Мінімальні витрати на функціонування системи управління запасами при даній стратегії складатимуть 85,4 тис. грн. ▲
(1,6 місяця). Мінімальні витрати на функціонування системи управління запасами при даній стратегії складатимуть 85,4 тис. грн. ▲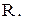
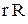 -стратегія.
-стратегія.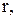 після чого фіктивний рівень запасів доводиться до рівня
після чого фіктивний рівень запасів доводиться до рівня 

 -моделі системи управління запасами з періодичними перевірками.
-моделі системи управління запасами з періодичними перевірками.
 врахованих незадовільнених замовлень у системі з періодичними перевірками за період Т визначається як середня величина попиту, коли він перевищує фіктивний рівень запасів
врахованих незадовільнених замовлень у системі з періодичними перевірками за період Т визначається як середня величина попиту, коли він перевищує фіктивний рівень запасів  -моделі від імовірності того, що запас в момент перевірки нижче рівня подачі замовлення
-моделі від імовірності того, що запас в момент перевірки нижче рівня подачі замовлення 
 шин/рік. Склад замовляє шини у виробника і час поставки приблизно постійний і дорівнює
шин/рік. Склад замовляє шини у виробника і час поставки приблизно постійний і дорівнює  місяцям. Величина сумарного попиту за час
місяцям. Величина сумарного попиту за час  із достатньою точністю описується нормальним законом розподілу із середнім
із достатньою точністю описується нормальним законом розподілу із середнім 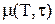 і середнім квадратичним відхиленням
і середнім квадратичним відхиленням 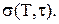 Кожна шина обходиться складу у
Кожна шина обходиться складу у 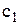 грн., а прийнятий на складі коефіцієнт витрат зберігання запасу складає І. Реєструються усі замовлення, які надійшли у той час, коли на складі не було запасів, і облік кожного замовлення обходиться у
грн., а прийнятий на складі коефіцієнт витрат зберігання запасу складає І. Реєструються усі замовлення, які надійшли у той час, коли на складі не було запасів, і облік кожного замовлення обходиться у 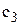 грн.
грн.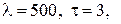
 ,
, 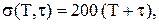


 грн., вартість перевірки
грн., вартість перевірки 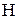 грн., вартість одиниці запасу
грн., вартість одиниці запасу 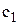 грн., коефіцієнт витрат зберігання запасів
грн., коефіцієнт витрат зберігання запасів  вартість обліку замовлень
вартість обліку замовлень 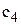 грн. у рік.
грн. у рік.

 Час поставки постійний і дорівнює
Час поставки постійний і дорівнює 
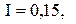
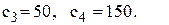

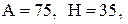
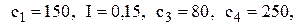
 тис. грн. Час поставки є випадковою величиною із середнім 0,1 року. Коефіцієнт витрат утримання запасу дорівнює І.
тис. грн. Час поставки є випадковою величиною із середнім 0,1 року. Коефіцієнт витрат утримання запасу дорівнює І.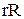 -стратегію управління запасами, визначити оптимальні значення фіктивного запасу
-стратегію управління запасами, визначити оптимальні значення фіктивного запасу 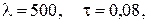


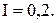 Величина попиту за будь-який час
Величина попиту за будь-який час  і дисперсією
і дисперсією  Час
Час 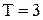 місяці;
місяці;

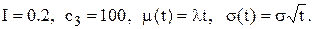
 Розгляньте два випадки: систему із обліком замовлень і систему із втратами замовлень.
Розгляньте два випадки: систему із обліком замовлень і систему із втратами замовлень.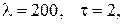


 Необслужені вчасно замовлення втрачаються, і кожне із цих втрачених замовлень обходиться у
Необслужені вчасно замовлення втрачаються, і кожне із цих втрачених замовлень обходиться у 

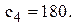
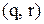 -моделі управління запасами, одержте середні за часом для різних показників у
-моделі управління запасами, одержте середні за часом для різних показників у 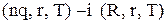 -моделях і покажіть, як ці середні за часом пов’язані із математичними сподіваннями тих же величин. Зокрема, покажіть, що середні річні витрати зберігання, середні втрати у наслідок дефіциту запасів тощо. дорівнюють відповідним середнім витратам за період, помноженим на
-моделях і покажіть, як ці середні за часом пов’язані із математичними сподіваннями тих же величин. Зокрема, покажіть, що середні річні витрати зберігання, середні втрати у наслідок дефіциту запасів тощо. дорівнюють відповідним середнім витратам за період, помноженим на 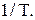 Крім того, покажіть, що середні річні витрати дорівнюють середнім витратам за цикл, помноженим на середнє число циклів у рік.
Крім того, покажіть, що середні річні витрати дорівнюють середнім витратам за цикл, помноженим на середнє число циклів у рік.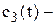 сума, у яку обходиться облік одного невиконаного замовлення, якщо з моменту його реєстрації пройшов час
сума, у яку обходиться облік одного невиконаного замовлення, якщо з моменту його реєстрації пройшов час  Спробуйте одержати вираз для середніх річних витрат на враховані замовлення, якщо попит розподілений за законом Пуассона.
Спробуйте одержати вираз для середніх річних витрат на враховані замовлення, якщо попит розподілений за законом Пуассона. -стратегія. Попит на матеріал можна вважати пуассонівським із середньою інтенсивністю
-стратегія. Попит на матеріал можна вважати пуассонівським із середньою інтенсивністю 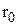 і після поставки
і після поставки 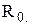 ;
;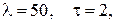






 13, 181
13, 181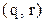 14
14 14, 211
14, 211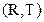 13, 206
13, 206 14
14


