
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Попит розподілений за законом пуассонаСодержание книги
Поиск на нашем сайте
Наведемо співвідношення для системи з обліком замовлень, вважаючи, що сумарний попит за будь-який проміжок часу розподілений за законом Пуассона, а час поставки залишається постійним і дорівнює Припустимо, що рівень запасів і попит є дискретними величинами. Нагадаємо, що згідно Визначимо спочатку стаціонарні ймовірності Обчислимо перехідні ймовірності Розглянемо випадок
Імовірність того, що попит за період дорівнює
При
Імовірності
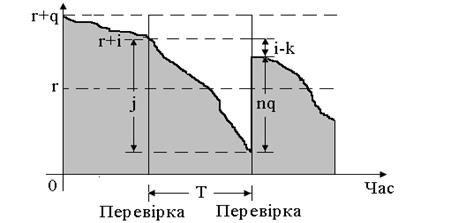
Рис. 5.2. Графік рівня запасів у Оскільки
Таким чином, у системах із періодичною перевіркою рівень запасів після закінчення перевірки розподілений рівномірно. Тепер можна продовжити виведення виразу для середніх річних витрат. Ми обмежимось тут випадком пуассонівського потоку замовлень одиничної величини. Крім того, будемо припускати, що вартість одиниці запасів постійна і не залежить від розміру замовлення. Припустимо, що
Спочатку ми обчислимо середні витрати за період, а потім, помноживши одержаний результат на Оскільки за рік здійснюється
Перетворюючи цей вираз, одержимо
Перейдемо до визначення середньої вартості врахованих за рік замовлень. Спочатку обчислимо середнє число замовлень, які враховані за період, а помноживши одержаний результат на Припустимо, що перевірка здійснюється в момент
а до моменту
Таким чином, якщо після перевірки в момент часу
Усереднюючи цей вираз по
Спрощуючи цей вираз, одержимо
де
і
Точно так можна обчислити середню інтегральну нестачу за рік. Для будь-якого моменту часу
а середня інтегральна нестача за один період визначається виразом
Усереднюючи цей вираз по
Застосовуючи формулу
одержуємо:
Далі маємо
Продовжуючи перетворення, середню інтегральну нестачу товару за рік
де
і
Таким чином, середні витрати за рік, пов’язані із обліком замовлень, дорівнюють
Для будь-якого моменту часу математичне сподівання обсягу наявного запасу дорівнює сумі математичного сподівання обсягу чистого запасу і математичного сподівання сумарного числа врахованих замовлень. Таким чином, середній обсяг наявного запасу в момент часу
Інтегруючи цей вираз у межах від
де Середній наявний запас у рік можна обчислити і іншим способом. У будь-який момент часу середній обсяг наявних запасів дорівнює математичному сподіванню фіктивного рівня запасів мінус середній обсяг ще непоставлених замовлень плюс математичне сподівання величини врахованого попиту. Для того щоб обчислити інтеграл по періоду від середнього рівня запасів, зручніше всього скористатись інтервалом часу між двома послідовними перевірками. Якщо в момент
Окрім того, помножений на Середній гарантійний запас (визначається за фіктивним рівнем запасу)
Усі складові сумарних річних витрат вже визначені. Підсумовуючи їх, одержимо наступний вираз
де
а
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 3; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.239.254 (0.009 с.) |

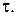
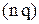 -стратегії, замовлення на поповнення подається тільки у тому випадку, коли під час перевірки виявляється, що фіктивний рівень запасів менше або дорівнює
-стратегії, замовлення на поповнення подається тільки у тому випадку, коли під час перевірки виявляється, що фіктивний рівень запасів менше або дорівнює  Якщо
Якщо 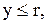 то замовляється поповнення на
то замовляється поповнення на  одиниць
одиниць  де
де  вибирається так, щоб
вибирається так, щоб 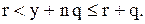 Таким чином, зразу ж після перевірки фіктивний рівень запасів прийме одне із значень
Таким чином, зразу ж після перевірки фіктивний рівень запасів прийме одне із значень 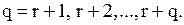
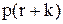 того, що зразу ж після перевірки фіктивний рівень запасів у системі складе
того, що зразу ж після перевірки фіктивний рівень запасів у системі складе 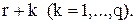 При умові, що попит у різні періоди незалежний, процес переходів із стану у стан можна вважати марковським ланцюгом із скінченим числом станів.
При умові, що попит у різні періоди незалежний, процес переходів із стану у стан можна вважати марковським ланцюгом із скінченим числом станів. де
де 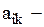 імовірність того, що зразу ж після чергової перевірки фіктивний рівень запасів складе
імовірність того, що зразу ж після чергової перевірки фіктивний рівень запасів складе 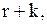 при умові, що після попередньої перевірки він дорівнював
при умові, що після попередньої перевірки він дорівнював  Позначимо
Позначимо  імовірність того, що за період між перевірками зі складу буде замовлено
імовірність того, що за період між перевірками зі складу буде замовлено 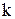 одиниць запасу.
одиниць запасу. Тоді із стану
Тоді із стану 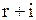 можна попасти у стан
можна попасти у стан 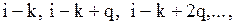 оскільки, якщо
оскільки, якщо  обсяг попиту за період, то для
обсяг попиту за період, то для  справедлива наступна рівність (див. рис. 5.1):
справедлива наступна рівність (див. рис. 5.1): або
або 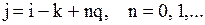
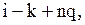 за означенням, є
за означенням, є 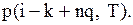 Оскільки події, які полягають у тому, що величина попиту прийме одне із певних значень, несумісні, то
Оскільки події, які полягають у тому, що величина попиту прийме одне із певних значень, несумісні, то
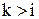 система може перейти у стан
система може перейти у стан  якщо попит за період буде рівним принаймні
якщо попит за період буде рівним принаймні 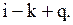 Таким чином,
Таким чином,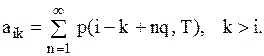
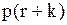 задовольняють наступним рівнянням:
задовольняють наступним рівнянням: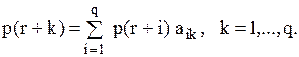
 -системі
-системі , то попереднім співвідношенням задовольняють постійні величини
, то попереднім співвідношенням задовольняють постійні величини  Крім того, із рівності
Крім того, із рівності 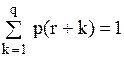 випливає, що
випливає, що

 вартість подачі замовлення на поповнення запасу;
вартість подачі замовлення на поповнення запасу; вартість однієї перевірки рівня запасів;
вартість однієї перевірки рівня запасів;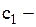 вартість одиниці запасів
вартість одиниці запасів коефіцієнт витрат зберігання запасів;
коефіцієнт витрат зберігання запасів; витрати зберігання запасу;
витрати зберігання запасу; витрати, пов’язані із обліком одного замовлення, де
витрати, пов’язані із обліком одного замовлення, де  час, який пройшов із моменту реєстрації замовлення;
час, який пройшов із моменту реєстрації замовлення; одержимо вираз для сумарних середніх річних витрат.
одержимо вираз для сумарних середніх річних витрат. перевірок, то середні річні витрати на перевірки складуть
перевірок, то середні річні витрати на перевірки складуть  За рік на замовлення витрачається сума, менша, ніж
За рік на замовлення витрачається сума, менша, ніж 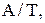 оскільки замовлення подаються не при кожній перевірці. І якщо
оскільки замовлення подаються не при кожній перевірці. І якщо  означає ймовірність подачі замовлення у довільний момент часу, то середні річні витрати на замовлення складуть
означає ймовірність подачі замовлення у довільний момент часу, то середні річні витрати на замовлення складуть  Обчислимо
Обчислимо  Якщо по закінченню перевірки фіктивний рівень запасів у системі дорівнює
Якщо по закінченню перевірки фіктивний рівень запасів у системі дорівнює  дорівнює ймовірності того, що попит за період перевищить або принаймні буде рівним
дорівнює ймовірності того, що попит за період перевищить або принаймні буде рівним 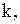 тобто ймовірності
тобто ймовірності  де
де  – середній попит за період Т. Імовірність того, що по закінченню перевірки рівень запасів дорівнює
– середній попит за період Т. Імовірність того, що по закінченню перевірки рівень запасів дорівнює  Звідси
Звідси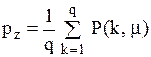 .
. (5.15)
(5.15)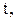 а наступна за нею перевірка – в момент
а наступна за нею перевірка – в момент  Обчислимо середнє число замовлень, врахованих на інтервалі від
Обчислимо середнє число замовлень, врахованих на інтервалі від 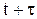 до
до  Загальне число врахованих на цьому інтервалі замовлень можна представити у вигляді різниці двох випадкових величин, одна із яких визначає число замовлень, врахованих до моменту
Загальне число врахованих на цьому інтервалі замовлень можна представити у вигляді різниці двох випадкових величин, одна із яких визначає число замовлень, врахованих до моменту  а друга дорівнює числу замовлень, врахованих до моменту
а друга дорівнює числу замовлень, врахованих до моменту  замовлень складає
замовлень складає
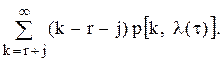
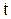 фіктивний рівень запасів у системі дорівнює
фіктивний рівень запасів у системі дорівнює  то математичне сподівання числа замовлень, врахованих на інтервалі від
то математичне сподівання числа замовлень, врахованих на інтервалі від 
 одержимо після множення на
одержимо після множення на  (5.16)
(5.16)
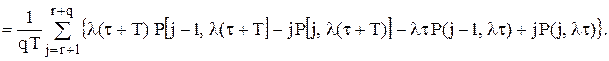
 (5.17)
(5.17)

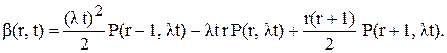
 такого, що
такого, що  середнє число врахованих замовлень при умові, що зразу ж після закінчення перевірки в момент
середнє число врахованих замовлень при умові, що зразу ж після закінчення перевірки в момент 
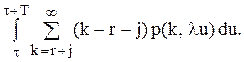
 знаходимо середню інтегральну нестачу за рік
знаходимо середню інтегральну нестачу за рік .
.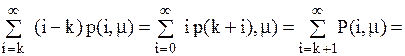
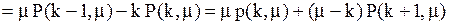 ,
,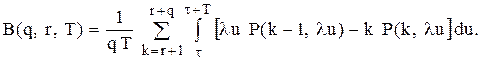 (5.18)
(5.18)

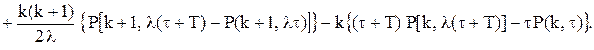
 можна представити у вигляді
можна представити у вигляді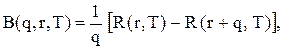 (5.19)
(5.19)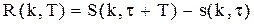
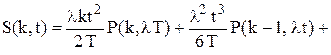
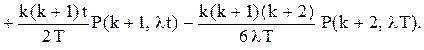
 Залишається обчислити середній обсяг наявних запасів у рік. Як і раніше, спочатку буде підрахована середня інтегральна нестача за період. Якщо в момент часу
Залишається обчислити середній обсяг наявних запасів у рік. Як і раніше, спочатку буде підрахована середня інтегральна нестача за період. Якщо в момент часу  такого, що
такого, що 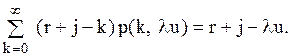

 до
до  і усереднюючи його по
і усереднюючи його по  (5.20)
(5.20)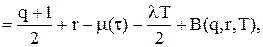
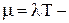 середній попит за час поставки. Цим же виразом визначається середній обсяг наявних запасів і для довільного моменту часу. Функції
середній попит за час поставки. Цим же виразом визначається середній обсяг наявних запасів і для довільного моменту часу. Функції 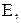
 і
і  у цьому розділі обчислювались інакше, ніж відповідні величини для
у цьому розділі обчислювались інакше, ніж відповідні величини для 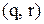 -моделей із розділу 4. Справа у тому, що тут ми маємо розподіл рівня запасів тільки в моменти закінчення перевірок, тоді як у випадку
-моделей із розділу 4. Справа у тому, що тут ми маємо розподіл рівня запасів тільки в моменти закінчення перевірок, тоді як у випадку  -моделей цей розподіл був відомий у будь-який момент.
-моделей цей розподіл був відомий у будь-який момент. де
де  складає
складає 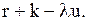 Інтегруючи цей вираз від 0 до
Інтегруючи цей вираз від 0 до  і усереднюючи його по
і усереднюючи його по 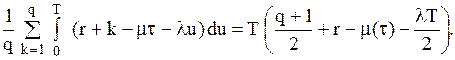
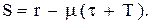 (5.21)
(5.21) (5.22)
(5.22)
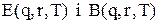 визначаються за формулами (5.17) і (5.18) відповідно.
визначаються за формулами (5.17) і (5.18) відповідно.


