
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Попит розподілений за нормальним закономСодержание книги
Поиск на нашем сайте
Алгоритм реалізації моделі v задаємо вхідні дані моделі v записуємо вираз для ймовірності розподілу Пуассона v визначаємо ймовірність подачі замовлення на поповнення запасу v визначаємо середню кількість врахованих за рік замовлень v визначаємо середню інтегральну нестачу товарів за рік v визначаємо середній запас за рік v визначаємо функцію середніх річних витрат Для знаходження оптимальних значень 1-й крок: Задаємо діапазон Перетворюючи масив значень функції 2-й крок: За знайденим оптимальним значенням параметра Далі, при знайденому оптимальному значенні Мінімальне значення функції Далі, визначаємо індекси Приклад 5.2. Розглянемо систему управління запасами, у якій використовується Визначимо оптимальну політику управління запасами у розглядуваній системі, використовуючи Алгоритм у Mathcad
Функціональні характеристики системи: Ø Середня кількість врахованих замовлень за рік Ø Середня інтегральна нестача товарів за рік Ø Середній обсяг запасу у системі за рік Ø Середній гарантійний запас Коментар. Оптимальна стратегія управління запасами у даній системі має такі параметри: Цей приклад показує, що R-стратегія еквівалентна nq-стратегії, і у тому випадку, коли ймовірність подачі замовлення при довільно вибраній перевірці мала, Розглянемо алгоритм реалізації Нехай Нехай
де
Тут
Звідси видно, що
то
Обчислимо тепер окремі складові загальних середніх річних витрат для випадку, коли попит розподілений за нормальним законом. На перевірки протягом року витрачається сума у
Звідси, приймаючи до уваги, що при наближенні розподілу ймовірностей за допомогою нормального розподілу значення щільності ймовірності і функції розподілу при Легко бачити, що середні річні витрати зберігання дорівнюють
де Визначимо тепер вирази для середньої кількості замовлень, які враховуються за рік, і для середньої інтегральної нестачі за рік. Для цього використовуються ті ж прийоми, що і у дискретному випадку, розглянутому у попередньому пункті. Середня кількість врахованих за рік замовлень складає
Далі маємо
Звідси одержуємо вираз для середньої кількості замовлень, врахованих за рік
де
Аналогічно одержуємо вираз для інтегральної середньої нестачі запасу
Визначення
Далі
Звідкіля
Загальні середні річні витрати тепер можуть бути записані у наступному вигляді:
де
а На жаль, функція Приклад 5.3. Розглянемо Визначимо оптимальну політику управління запасами у даній системі, використовуючи Загальний алгоритм реалізації даної моделі аналогічний алгоритму попередньої моделі. Відповідні параметри нормального розподілу попиту дорівнюють
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.128 (0.007 с.) |


 і його функцію розподілу
і його функцію розподілу 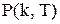 ;
;

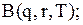

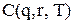 .
.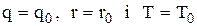 застосуємо алгоритми дискретної оптимізації (перебірні алгоритми).
застосуємо алгоритми дискретної оптимізації (перебірні алгоритми).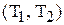 можливих значень параметра
можливих значень параметра 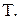
 для
для 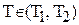 у матрицю
у матрицю 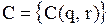 , визначаємо мінімальний елемент цієї матриці
, визначаємо мінімальний елемент цієї матриці  , його індекси і за ними оптимальні значення
, його індекси і за ними оптимальні значення 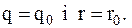
 визначаємо оптимальні
визначаємо оптимальні 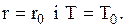
 задаємо діапазони зміни параметрів
задаємо діапазони зміни параметрів  , відповідно
, відповідно 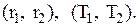 Представляємо масив значень функції
Представляємо масив значень функції 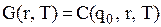 у вигляді матриці
у вигляді матриці 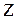 , елементи якої
, елементи якої  де
де 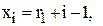

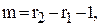

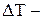 крок зміни параметра Т,
крок зміни параметра Т, 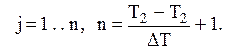
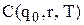 знаходимо як мінімальний елемент
знаходимо як мінімальний елемент  матриці
матриці  .
.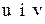 мінімального елемента матриці
мінімального елемента матриці 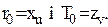 Визначаємо гарантійний запас
Визначаємо гарантійний запас 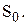
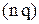 -стратегія, а попит розподілений за законом Пуассона із середньою інтенсивністю
-стратегія, а попит розподілений за законом Пуассона із середньою інтенсивністю  одиниць/рік. Час поставки постійний і дорівнює 0,25 року. Інші параметри мають такі значення :
одиниць/рік. Час поставки постійний і дорівнює 0,25 року. Інші параметри мають такі значення :  ,
,  ,
,  ,
, 
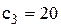 і
і  грош. од. у рік. Відмітимо, що подача замовлення обходиться у два рази дорожче перевірки. Якщо вартість замовлення значно менше вартості перевірки, то ми можемо очікувати, що
грош. од. у рік. Відмітимо, що подача замовлення обходиться у два рази дорожче перевірки. Якщо вартість замовлення значно менше вартості перевірки, то ми можемо очікувати, що 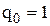 і
і  -модель еквівалентна
-модель еквівалентна  -моделі. Але у тому випадку, коли вартість замовлення вище вартості перевірки, то можна розраховувати на те, що
-моделі. Але у тому випадку, коли вартість замовлення вище вартості перевірки, то можна розраховувати на те, що  більше одиниці. У даному прикладі розглядається перший випадок.
більше одиниці. У даному прикладі розглядається перший випадок.
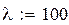
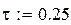









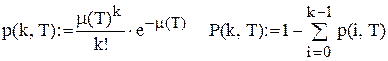

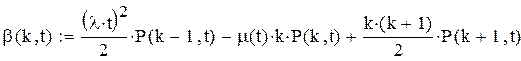

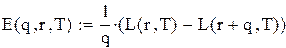


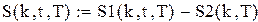

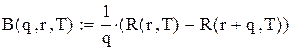
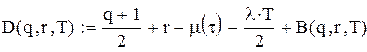
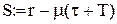


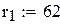
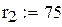
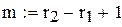
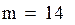



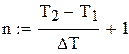
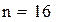

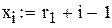


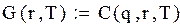






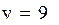

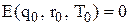 ;
; ;
;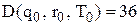 ;
; .
. Інші характеристики системи: середня кількість врахованих замовлень за рік
Інші характеристики системи: середня кількість врахованих замовлень за рік  середня інтегральна нестача товарів за рік
середня інтегральна нестача товарів за рік 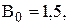 середній обсяг гарантійного запасу у системі за рік
середній обсяг гарантійного запасу у системі за рік 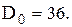 Мінімальне значення середніх річних витрат при даній стратегії управління
Мінімальне значення середніх річних витрат при даній стратегії управління 
 -модель забезпечує суттєве зниження витрат у порівнянні з
-модель забезпечує суттєве зниження витрат у порівнянні з  -моделлю. Сюди відносяться ті випадки, коли період перевірки настільки малий, що система з періодичною перевіркою за характером процесів, які в ній протікають, подібна системі з оперативною інформацією. У таких ситуаціях розмір партії поповнення запасу
-моделлю. Сюди відносяться ті випадки, коли період перевірки настільки малий, що система з періодичною перевіркою за характером процесів, які в ній протікають, подібна системі з оперативною інформацією. У таких ситуаціях розмір партії поповнення запасу  -стратегія буде переважати
-стратегія буде переважати  -стратегією. У цьому випадку для визначення оптимальних значень
-стратегією. У цьому випадку для визначення оптимальних значень 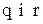 майже завжди можна користуватись
майже завжди можна користуватись 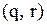 -моделлю. ▲
-моделлю. ▲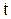 є неперервна випадкова величина розподілена за нормальним законом із середнім
є неперервна випадкова величина розподілена за нормальним законом із середнім  і дисперсією
і дисперсією  Будемо також припускати, що величини
Будемо також припускати, що величини 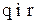 також неперервні.
також неперервні. є щільність розподілу величини попиту за період
є щільність розподілу величини попиту за період  означає стаціонарну ймовірність події, яка полягає у тому, що фіктивний рівень запасів після закінчення перевірки вміщений у межах
означає стаціонарну ймовірність події, яка полягає у тому, що фіктивний рівень запасів після закінчення перевірки вміщений у межах 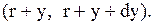 Можна показати, що щільність
Можна показати, що щільність 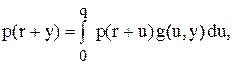 (5.23)
(5.23)
 , якщо
, якщо  якщо
якщо 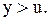 Зауважимо, що
Зауважимо, що
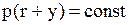 при
при 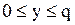 є розв’язком рівняння (5.23). А оскільки
є розв’язком рівняння (5.23). А оскільки
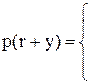
 (5.24)
(5.24) грош. одиниць, закази обходяться у середньому у
грош. одиниць, закази обходяться у середньому у  грош. одиниць у рік. Тут
грош. одиниць у рік. Тут  є ймовірність того, що при довільній перевірці подається заказ. Ця ймовірність дорівнює
є ймовірність того, що при довільній перевірці подається заказ. Ця ймовірність дорівнює
 досить близькі до нуля, одержимо
досить близькі до нуля, одержимо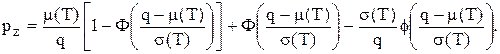 (5.25)
(5.25) (5.26)
(5.26)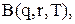 як і раніше, середня інтегральна нестача за рік, тобто середня кількість врахованих невиконаних замовлень.
як і раніше, середня інтегральна нестача за рік, тобто середня кількість врахованих невиконаних замовлень. (5.27)
(5.27)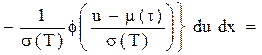
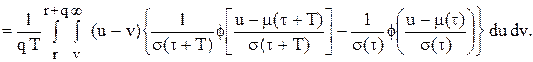


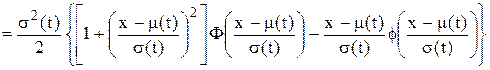 .
.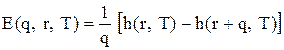 , (5.28)
, (5.28) .
.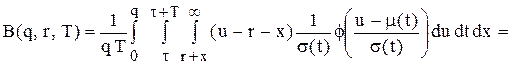 (5.29)
(5.29) .
. проводиться у декілька етапів. Спочатку одержуємо
проводиться у декілька етапів. Спочатку одержуємо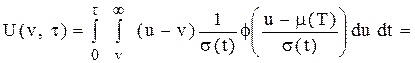 (5.30)
(5.30)


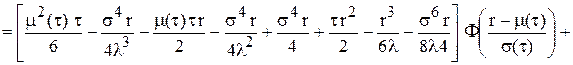



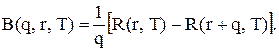 (5.31)
(5.31)
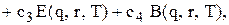 (5.32)
(5.32)
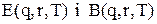 визначаються за формулами (5.28) і (5.29) відповідно.
визначаються за формулами (5.28) і (5.29) відповідно.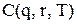 у загальному випадку не є опуклою функцією
у загальному випадку не є опуклою функцією 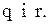 Це ускладнює задачу обчислення оптимальних значень
Це ускладнює задачу обчислення оптимальних значень 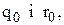 оскільки у функції
оскільки у функції  досить складно. Таким чином, як і у дискретному випадку для знаходження оптимальних
досить складно. Таким чином, як і у дискретному випадку для знаходження оптимальних  . Усі інші параметри моделі такі ж самі, як і у прикладі 5.2.
. Усі інші параметри моделі такі ж самі, як і у прикладі 5.2.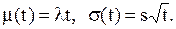 Наведемо алгоритм реалізації моделі у Mathcad.
Наведемо алгоритм реалізації моделі у Mathcad.


