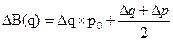Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексный метод факторного анализаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сущность индексного метода факторного анализа состоит в следующем: во-первых, определяются индекс результативного показателя и индексы факторов; во-вторых, устанавливается схема взаимосвязи индекса результативного показателя с индексами факторов; в-третьих, составляется алгоритм расчетов влияния факторов на изменение результативного показателя. Рассмотрим применение индексного метода факторного анализа на примере. Имеем информацию о выручке от продаж в торговой точке за два аналогичных периода времени. Базовый вариант: В0 = q0*p0- B0 =10 тыс. шт. х 6 руб. = 60 тыс. руб. Отчетный вариант: В1 = q1*p1 В1 = 12 тыс. шт. х 9 руб. = 108 тыс. руб. ΔВ = В1 - Во = 108 - 60 = +48 тыс. руб. Рассчитаем индексы результативного показателя и индексы факторов:
Взаимосвязь индекса результативного показателя с индексами факторов аналогична взаимосвязи самого результативного показателя с факторами, т.е. IB= Iq * Ip →1.8 = 1,2 х 1,5. Алгоритм I расчетов влияния факторов индексным методом 1) влияние на выручку изменения количества проданного товара ΔВ(q)=(Iq- 1)* B0 3) влияние на выручку изменения цены единицы товара ΔВ(p)=(Iq * Ip –Ip)* B0 Проверка: ΔВ = В1 - Во = ΔВ (q) + ΔВ(р). Расчеты влияния факторов: 1) ΔВ (q) = (1,2- 1,0) х 60 тыс. руб. = +12 тыс. руб.; 2) ΔВ (р) = (1,2 х 1,5- 1,2) х 60 тыс. руб. = +36 тыс. руб. Проверка: ΔВ = 108 - 60 = 12 + 36, или 48 тыс. руб. = 48 тыс. руб. Достоинство индексного метода состоит в том, что изменение результативного показателя раскладывается по факторам без остатка. Вместе с тем этому методу свойственен серьезный недостаток — элемент субъективизма. Он заключается в произвольном определении порядка расположения факторов в цепочке сомножителей. Рассмотренный выше алгоритм соответствует только одному варианту расположения факторов, т.е. B =q*p С позиций математики равноправным является и другой вариант расположения факторов, т.е. В = р х q. Однако второму варианту расположения факторов соответствуют другой алгоритм и другие результаты расчетов. Алгоритм, 2 расчетов влияния факторов индексным методом 1) влияние на выручку изменения цены единицы товара ΔВ (р) = (Ip -1)хВ0; 2) влияние на выручку изменения количества проданного товара ΔВ (q) = (/р х Iq - /р) х Во. Проверка: ΔВ = В1 - Во = ΔВ (р) + ΔВ (q). Расчеты влияния факторов: 1) ΔВ (р) = (1,5 - 1,0) х 60 тыс. руб. = +30 тыс. руб.; 2) ΔВ (q) = (1,5 х 1,2 - 1,5) х 60 тыс. руб. = +18 тыс. руб. Проверка: ДВ = 108 - 60 = 30 + 18, или 48 тыс. руб. = 48 тыс. руб. Таким образом, результаты расчетов влияния факторов по двум вариантам не совпадают. Причиной несовпадения является «неразложенный остаток». В первом варианте он «присоединился» к фактору «изменение цены единицы товара». Во втором — к фактору «изменение количества проданного товара». С увеличением числа факторов-сомножителей резко возрастает количество равноправных вариантов расчетов, так как увеличивается число возможных перестановок факторов. Например, число перестановок из трех по три равно шести, из четырех по четыре — 24, а из пяти по пять — 120. Для обоснования правильности только одного из многих вариантов экономисты вывели следующее правило индексного метода факторного анализа. Все факторы можно разделить на две группы: 1)количественные (первичные, или экстенсивные); 2)качественные (вторичные, или интенсивные). При расстановке факторов в модели исходят из следующего: на первое место ставится количественный фактор, на второе — качественный. В соответствии с этим положением следует признать правильным первый из рассмотренных нами алгоритмов. Вместе с тем необходимо помнить, что данное правило субъективно. Для лучшего понимания сущности индексного метода приведем алгоритм расчетов для решения трехфакторной мультипликативной модели. Алгоритм расчетов влияния факторов индексным методом для решения трехфакторной мультипликативной модели Базовый вариант: QQ = а0 * b0 * с0. Отчетный вариант: Q1 = а1 * b1 * с1. Δ Q= Q1 -QQ Расчеты влияния факторов: l) Δ Q(a) = (Ia-1)xQ0; 2) Δ Q(b) = (Ia *lb- Ia) x Qo; 3) Δ Q(c) = (Ia *lb*lc Ia) x Qo Q1 - Qo = Δ Q(a) + Δ Q(b) + Δ Q(c).
Метод цепных подстановок
Метод цепных подстановок является производным от индексного метода факторного анализа. Его суть состоит в следующем. Для расчета влияния факторов на изменение результативного показателя определяется условная величина (подстановка), отражающая, каков был бы результативный показатель, если бы один фактор изменился, а другие остались бы неизменными. Если в модели число факторов-сомножителей более двух, то приходится определять несколько взаимосвязанных подстановок (цепочку подстановок). Отсюда название — метод цепных подстановок. Алгоритм 1 расчетов влияния факторов методом цепных подстановок Сумма влияния двух факторов равняется изменению результативного показателя: В1 - Во = Δ B(q) + Δ В(р). Расчеты влияния факторов: 1)влияние на выручку изменения количества проданного товара 2)влияние на выручку изменения цены единицы товара
Достоинство метода цепных подстановок, как и индексного метода, состоит в том, что изменение результативного показателя раскладывается по факторам без остатка. Вместе с тем методу цепных подстановок присущ элемент субъективизма, который заключается в выборе порядка расположения факторов в цепочке сомножителей. Рассмотренный выше алгоритм соответствует только одному варианту расположения факторов, т.е. B =q*p С позиций математического подхода равноправным является и другой вариант расположения факторов, т.е. В = р х q. Однако второму варианту расположения факторов соответствуют другой алгоритм и другие результаты расчетов. Алгоритм 2 расчетов влияния факторов методом цепных подстановок Расчеты влияния факторов: 1) влияние на выручку изменения цены единицы товара 2) влияние на выручку изменения количества проданного товара
Для обоснования правильности одного из многих вариантов экономисты вывели следующее субъективное правило метода цепных подстановок. Влияние изменения на результативный показатель количественного фактора подсчитывается при базовом значении качественного фактора, т.е. ΔВ(q) = Δq*p0 Влияние изменения на результативный показатель качественного фактора определяется при отчетном значении количественного фактора, т.е. ΔВ(p) = Δp*q1 С позиций данного правила следует признать обоснованным первый из двух рассмотренных алгоритмов. Вместе с тем нужно помнить, что это правило субъективно. Для более полной иллюстрации сущности метода цепных подстановок приведем алгоритм расчетов влияния факторов на результативный показатель для трехфакторной мультипликативной модели. Алгоритм расчетов влияния факторов методом цепных подстановок для решения трехфакторной мультипликативной модели Базовый вариант QQ = а0 * b0 * с0. Отчетный вариант: Q1 = а1 * b1 * с1. Δ Q= Q1 -QQ Расчеты влияния факторов: 1) Δ Q(a) = Δ а * b0 * с0 2) Δ Q(b) = а1 * Δ b * с0 3) Δ Q(c) = а1 * b1 * Δ с Q1 - Qo = Δ Q(a) + Δ Q(b) + Δ Q(c). При практическом применении цепных подстановок возникли различные модификации этого метода, предназначенные для упрощения расчетов, — способ абсолютных отклонений, способ относительных отклонений, способ процентных разниц. 3.8. Интегральный метод факторного анализа Интегральный метод факторного анализа применяется в,тех случаях, когда результативный показатель может быть представлен как функция от нескольких аргументов. Изменения функции в зависимости от изменения аргументов описываются соответствующими интегральными выражениями. При проведении факторного анализа интегральный метод может быть использован для решения двух типов задач [5]. К первому типу относятся такие задачи, в которых отсутствует информация об изменении факторов внутри анализируемого периода либо от этого изменения можно абстрагироваться. В данном случае величина изменения результативного показателя не зависит от порядка расположения факторов в модели. Этот тип задач называется статическим. В качестве примера можно привести сравнительный анализ показателей двух аналогичных объектов. Второй тип задач связан с анализом показателей в динамике, т.е. когда имеются данные об изменении факторов внутри анализируемого периода. Интегральный метод факторного анализа дает общий подход к решению задач разного типа независимо от количества факторов, входящих в модель, схемы взаимосвязи между ними и порядка расположения факторов в модели. Этот метод позволяет осуществить расчеты влияния факторов на результативный показатель в мультипликативных, кратных и смешанных моделях без образования «неразложенного остатка». Применение интегрального метода дает возможность получить однозначные результаты расчетов влияния факторов на изменение результативного показателя. При использовании интегрального метода изменение выручки от продаж можно представить как сумму двух интегралов. Один из них характеризует зависимость выручки от количества проданного товара, а другой — от цены единицы товара. Алгоритмv расчетов влияния факторов интегральным методом для решения двухфакторной мультипликативной модели Базовый вариант: Во = qQ x р0. Отчетный вариант: B1 = q1x р1. Δ В = В1-В0= где f'(q), f'(p) — функции изменения выручки в зависимости соответственно от количества проданного товара и цены его единицы. Исходя из предположения, что данные факторы в пределах небольшого промежутка времени изменяются по линейному закону, расчеты влияния факторов на изменение выручки можно представить следующим образом: 1) влияние изменения количества проданного товара
3) влияние изменения цены единицы товара 4)
Однако интегральный метод также имеет существенный недостаток: с увеличением в модели числа факторов-сомножителей резко повышается сложность вычислений, т.е. возрастают объем и трудоемкость расчетов влияния каждого фактора на изменение результативного показателя. Рассмотрим алгоритм расчетов влияния факторов интегральным методом для решения трехфакторной мультипликативной модели. Алгоритм расчетов влияния факторов интегральным методом для решения трехфакторной мультипликативной модели
В практике аналитической работы интегральный метод не получил широкого распространения. Он используется преимущественно в научно-исследовательских разработках в области экономического анализа.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

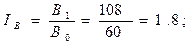
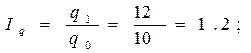

 Проверка: Δ В = 108 - 60 = 12 + 36, или 48 тыс. руб. = 48 тыс. руб.
Проверка: Δ В = 108 - 60 = 12 + 36, или 48 тыс. руб. = 48 тыс. руб. Проверка: ΔВ = 108-60 = 30+ 18, или 48 тыс. руб. = 48 тыс. руб.
Проверка: ΔВ = 108-60 = 30+ 18, или 48 тыс. руб. = 48 тыс. руб.