Модель Солоу и попытки ее применения к развивающимся странам

Институциональная критика теории роста не осталась незаме­ченной неоклассиками. Особенно большое воздействие на них оказала теория человеческого капитала², которую они и попыта­лись включить в свои модели. Это было тем более необходимо, так как критика неокейнсианских моделей со стороны У.А Льюиса была недостаточной. Неоклассические теории роста получили солидное основание благодаря работам Р. Солоу.

5"9tt"24239"002401 61

¹ См.- Вопросы экономики. 2000. № 4-7.

² О становлении концепции человеческого капитала подробнее см.: Капелюш-
ников Р.И. Современная буржуазная концепция формирования рабочей силы (кри­
тический анализ). М.: Наука, 1981.

Роберт Мертон Солоу родился в Нью-Йорке в 1924 г После окон­чания школы получил стипендию для обучения в Гарвардском университете. Однако его учеба была прервана второй мировой войной. В 1945 г. Солоу вернулся в Гарвардский университет, где продолжил обучение под руководством Василия Леонтьева.

Закончив аспирантуру Колумбийского университета, получил приглашение в Массачусетский технологический институт (MIT) в 1954 г., где и проработал профессором всю жизнь. За работы по теории экономического роста Роберт Солоу получил в 1987 г. Нобелевскую премию по экономике.

Сформулированная им в 50-60-е годы концепция привела к замене кейиспанской модели Харрода—Домара неоклассической теорией роста. Для понимания особенностей применения модели Солоу в развивающихся странах кратко рассмотрим ее основные черты³.

5.1.1. Модель Солоу

1-й

Р. Солоу наглядно показал, что нестабильность динамического равновесия в неокеииспанских моделях была прежде всего след­ствием невзаимозаменяемости ресурсов. Поэтому вместо функции В.Леонтьева он использовал производственную функцию Кобба— Дугласа, в которой, как известно, труд и капитал являются субсти­тутами.

О < а < I.

/(*)

Рис. 5.1. Производственная функция

Классическая мо­дель Солоу исходит из убывающей про­изводительности ка­питала, постоянной отдачи от масштаба (сумма коэффициен­тов при К и L равня­ется 1), неизменной нормы выбытия (амор­тизации) и отсутствия инвестиционных ла­гов. Взаимозаменяе­мость факторов про-

³ Модель впервые опубликована в. Solow R A Contribution to the Theory of Economic Growth//Quarterly Journal of Economics. 1956. February. P. 65-94.

изводства объясняется не только технологическими условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках ресурсов.

Особенностью использования функции Кобба—Дугласа в моде­ли Солоу является то, что все параметры (производительность, ка­питаловооруженность и др.) рассматриваются на единицу труда. Поэтому он обозначает у = Y/L, к = K/L, где у — выпуск, а к — капитал на одного работника: у = f(k).

Тангенс угла наклона производственной функции соответству­ет предельному продукту капитала МР_к, который убывает по мере роста капиталовооруженности (рис. 5.1).

Поскольку государственные закупки не учитываются, совокуп­ный спрос определяется инвестициями и потреблением:

y = i + c, (2)

где с — потребление;

/ — инвестиции в расчете на единицу труда

c = (\-s)y, (3)

где 5" — норма сбережения (накопления).

у = / + (1 — s) у => i = sy. (4)

Это означает, что в условиях равновесия инвестиции равны сбережениям и пропорциональны доходу. А так как у = /(к), то i = sf(k) (рис. 5.2).

/(*)

Поскольку в модели Солоу предполагается постоянная норма выбытия, то она пропорциональна капиталу Ьк и может быть изоб­ражена лучом, выходящим из начала координат с угловым коэф­фициентом 8 (рис. 5.3). В условиях равновесия инвестиции равны вы­бытию: sf{k) = Ьк. Рав­новесный уровень капи­таловооруженности обо­значается к* (рис. 5.4).

Равновесие в модели Солоу устойчиво. Это означает, что, если воз­никает несоответствие инвестиций выбытию, модель стремится к рав­новесному состоянию.

Если к, < к*, то валовые _{Рис 5 2} производство, потребление

инвестиции будут больше _и инвестиции в модели Солоу

 

Рис. 5.3. Выбытие капитала

\k выбытия: sf(k) > Ьк. Сле­довательно, чистые инве­стиции увеличат запас ка­питала, в результате чего капиталовооруженность возрастет и Л, -> к*. На­оборот, если к₂ -> к*, то валовые инвестиции _^ будут меньше выбытия: к sf(k) < Ьк. Следовательно, чистые инпестиции (будучи отрицательными) умень­шат запас капитала, в результате чего капиталовооруженность снизится и к₂ —> к* (рис. 5.5).

Норма сбережения непосред­ственно влияет на устойчивый уровень капиталовооруженности труда. Рост нормы сбережения (например, от я, до s₂) сдвинет кривую инвестиций вверх из положения s_if(k) до s₂f(k) (рис. 5.6). Соответственно эго приведет к увеличению устойчи­вого уровня капиталовооружен-

2 -

Рис. 5.4. Равновесный рост в модели Солоу

Л| к к | к к} к-} к Рис. 5.5. Устойчивость равновесного роста в модели Солоу

ности с к.* до к

 

к *

Рис. 5.6. Увеличение нормы сбережения

Рост нормы сбережения в краткосрочном периоде при­ведет к ускорению экономи­ческого роста и будет продол­жаться до тех пор, пока эко­номика не достигнет точки нового устойчивого равновесия. Несмотря на очевидные достоинства, модель Солоу обладает рядом недостатков. Несомненно, что ни процесс накопления, ни повышение нормы сбережения не объ­ясняют сам механизм непрерывного экономического роста. Они лишь показывают возможность перехода от одного состояния рав­новесия к другому. Поэтому Солоу вводит в модель рост населения и технический прогресс. Очевидно, что рост населения, как и вы­бытие, снижает капиталовооруженность, так как наличный запас капитала должен распределяться между возросшим числом занятых. Если же мы хотим не только поддерживать существующий уро­вень производительности труда, но и увеличивать его эффектив­ность, необходимо выделять дополнительные средства на повыше­ние капитачовооруженности. Все это приведет к тому, что угол

Рис. 5.7. Равновесный рост с учетом роста населения и технического прогресса

наклона луча, выходя-{«+ g + 5) к шего из начала коорди­нат, будет включать не только выбытие (5), но темпы роста населения (я) и технический про­гресс (g)⁴. Устойчивое равновесие с учетом роста населения и тех­нического прогресса показано на рис. 5.7,

Модель Солоу опре­деляет устойчивое рав-

новесие в долгосрочном периоде, объясняя его техническим про­грессом как единственной основой устойчивого роста благососто-

⁴ В модели Солоу предполагается, что темпы роста населения и технического прогресса постоянны (л, д — const). Подробнее см.: Манкью Г. Макроэкономика. М.: Изд-во МГУ, 1994. Гл. 4; Romer D. Advanced Macroeconomics. The McGraw-Hill Companies, Inc.. 1996. Ch. 1. P. 5-32; Ша ас Н.Л., Туманова Е.А. Макроэкономика-2. Долгосрочный аспект. М.. Теис. 1997. С. 63-78; Кавицкая И.Л., Шараев Ю.В. Макроэкономика-2. Ч. 3. М.: ГУ-ВШЭ. 1999. С. 11-26.

 

1-2618

яния. Между тем, для экономической политики важен прежде всего краткосрочный аспект: динамика производства и уровня жизни li ближайшей перспективе. От этого зависит и популярность прави­тельства, и возможность его переизбрания.

Многие переменные (s, 6, п, g) определяются в модели Солоу экзогенно, поэтому дальнейшие попытки усовершенствования модели были снизаны с превращением их в эндогенные. К тому же модель носит довольно общий характер и не учитывает целый ряд реальных ограничителей экономического роста (социальных, экологических и т. д.).

Несмотря на это, было предпринято несколько попыток для ее конкретизации в «третьем мире». Рассмотрим некоторые из них.

Очевидно, что повышение темпов роста населения приведет к снижению устойчивого уровня капиталовооруженности. Высокие темпы роста населения типичны для развивающихся стран. Не­удивительно, что в «третьем мире» более высокие темпы роста населения приводят к тому, что устойчивый уровень капиталово­оруженности устанавливается на более низком, чем в развитых странах, уровне (рис. 5.8).

скромной. В Латинской Америке и Африке она была нулевой, в Южной Азии составила 0,6% в год, в Восточной Европе, Северной и Восточной Африке она достигла 1,4% и лишь в Восточной Азии приблизилась к 2% (табл. 5.1).

Таблица 51

Вклад факторов производства в экономический рост (для 68 развивающихся стран, 1960-1987 гг., в % в год)

 

Регионы	Рост ВВП	Вклад труда	Вклад капитала	Общая производи­тельность факторов
Африка	3.3	1.0	2,3	0,0
Восточная Азия	6,8	1.1	3,8	1.9
Восточная Европа, Восточная и Северная Африка	5,0	0,7	2,9	1.4
Латинская Америка	3,6	1.2	2.4	0.0
Южная Азия	4,4	0,9	2.9	0.6
Для всех 68 стран	4,2	1,0	2,6	0,6

 

к* к₀* k(t)

Рис 5 8 Влияние роста населения на устойчивый уровень капиталовооруженности

Исследования Всемирного банка, проведенные в 68 развива­ющихся странах, показали, что наибольший вклад в повышение темпов роста внесло увеличение затрат ресурсов — капитала и труда, тогда как общая производительность факторов оказалась более чем

Источник: World Bank, World Development Report. Washington, DC: The World Bank. 1991.

Исследования африканских стран с середины 60-х до начала 80-х годов, проведенные Е. Шааелдином, показали еще более удручающие результаты. Общие темпы роста производительности в Кении, Танзании и Замбии были отрицательные, а в Зимбабве едва отличались от нуля (табл. 5.2).

Таблица 52

Вклад факторов производства в промышленный рост (для некоторых стран Африки, в % в год)

 

Страны	Рост выпуска	Вклад труда	Вклад капитала	Общий рост производительности
Кения 1964-1983	7.99	1,99	6,89	-0,89
Танзания 1966-1980	8,06	3 16	5,41	0 51
Замбия 1965-1980	4,98	1,20	9,38	-6.60
Зимбабве 1964-1981	5,28	1,88	3,39	+0.03

Источник: Shaueldin E. Sources of Industrial Growth in Kenya, Tanzania, Znmbia and Zimbabwe: Some Estimates//African Development Review. (989. June. Цит. по: Thirlwall A.P Growth and Development. With Especial Reference to Development Economics. 6^lhed. L.: Macmillan Press Ltd., 1999. P. N5.

 

 

5.1.2. Проблема сходимости

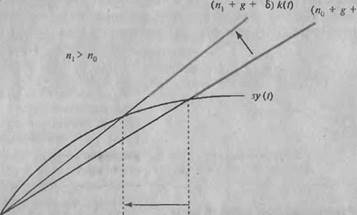
Важное значение в модели Солоу имеет тезис о сходимости (конвергенции). Действительно, если две страны имеют одинако­вую производственную функцию, темп роста населения, норму выбытия и норму сбережения, то очевидно, что они стремятся к одному и тому же устойчивому уровню капиталовооруженности к*. Естественно, что развивающаяся страна имеет первоначальный уровень капиталовооруженности (Л,) более низкий, чем развитая {к₂), и обе страны имеют уровень капиталовооруженности ниже рапновесного {к*): Л, < к₂< к*. Это означает, что она должна иметь

первоначально и более высокие темпы роста кап итал овооруже н нос-ти: g_kl >g_k2 (рис. 5.9). Очевидно, что по мере приближения к устой чивому уровню капи­таловооруженности темп прироста капи­таловооруженности будет уменьшаться, а следовательно, будет уменьшаться и темп роста экономики в целом.

Гипотеза о строгой (абсолютной) сходимости объясняет тот факт, что при наличии указанных выше предпосылок страны с первона­чально меньшим запасом капитала развиваются быстрее, чем страны с большим первоначальным запасом капитала. Однако на практике такая абсолютная сходимость маловероятна. Поэтому обычно для проверки модели Солоу исходят из гипотезы о слабой (условной) сходимости. Это означает, что каждая страна имеет свой устойчи­вый уровень капиталовооруженности (£,* < /с₂*), т.е. снимается предпосылка об одинаковой норме сбережения, оставляя все другие без изменения.

Если норма сбережения в развивающейся стране {s_{) меньше, чем норма сбережения в развитой стране (s₂), то темп прироста капиталовооруженности может быть больше, меньше или ранен темпу прироста капиталовооруженности в развитой стране. На рис. 5.10 показан случай, когда £*,<£*₂. При этом сходимость достигается отнюдь не всегда.

\

я +6

А, кг к* к Рис. 5.9. Гипотеза о строгой (абсолютной) сходимости

 

/7+6

Рис. 5.10. Гипотеза о нестрогой (условной) сходимости

Модель Солоу исхо­дит из постоянного темпа роста населения, однако в реальной действитель­ности темпы роста насе­ления могут меняться. Естественный прирост населения и (что осо­бенно нажно в модели Солоу) прирост населе­ния в трудоспособном возрасте зависят не только от уровня рожда­емости и смертности, но и от темпов эмиграции.

Они MOiyr быть положительными, нулевыми и отрицательными. Их изменения могут привести к тому, что пк может представлять собой не луч, выходящий из начала координат, а кривую.

Отложим на оси абсцисс капиталовооруженность труда (к), а на оси ординат ожидаемые сбережения на единицу труда {sy) и инвес­тиции, необходимые на единицу труда {пк) (рис. 5.11). В условиях изменения темпов прироста населения в трудоспособном возрасте возможно установление равновесия при различных уровнях капи­таловооруженности (А,*, £*), одни из которых будут устойчивы, а другие нет. В данном примере Е_о — устойчивое равновесие, F_x — неустойчивое равновесие. Таким образом, устойчивое равно­весие, предполагаемое в классической модели Солоу, отнюдь не всегда достижимо в «третьем мире».

Sy, пк

Рис. 5.11. Различные варианты роста населения в модели Солоу Источник: Hess P., Ross С. Economic Development: Theories. Evidence and Policies. Philadelphia etc., 1997. P. 107.

(10) (И) (12) (13) (14)

(15)

5.1.3. Мэнкью-Ромер-Уэйл:

тестирование модели Солоу

В 80-90-е годы появляются многочисленные попытки уточнить и дополнить модель Солоу. Однако при этом возникает ряд вопро­сов, связанных как с самой моделью, так и с применяемыми для ее пронерки статистическими данными.

Какую часть реального роста объясняет сама модель? Действи­тельно ли (и если да, то в какой степени) объясняющие перемен­ные являются экзогенными? В какой мере темпы роста населения, технического прогресса и обновления капитала не зависят от су­ществующего в обществе уровня развития производительных сил (выработки на одного рабочего)?

Применение ее в чистом виде для развивающихся стран не может дать таких же результатов, как для развитых стран, поскольку мо­дель делает акцент на капиталоемких технологиях (типичных для передовых стран) и основу технического прогресса видит прежде всего в росте капиталовооруженности труда.

Поэтому неудивительно, что верификация модели применитель­но к развивающимся странам создает такие сложности, которые незнакомы развитому миру. Чтобы в этом убедиться, рассмот­рим попытку, предпринятую в 1992 г. Г. Мэнкью, Д. Ромером и Д. Уэйлом⁵.

Они рассматривают ее в следующем виде:

 

В состоянии устойчивого равновесия

k(t) = sk(t)^a -(«+ £ + b)k(t) = О

** =

(I-a)

n + g + b)

_L__ _v*__fA:*4a I___ •>_

AL~^{y [K)} [n + g + b)

Прологарифмируем (13)

1п(л + g + 8)

1-a

ln|-^-|=

AL) 1-a

In

/1(0 ДО Lit) у™ "ДО Учитывая, что A(t) = А{0)е&, получим In A(t) = In A(0) + gt

 

Й

0<а<1

(5)

ln-^y = ln/l(O) + g/

a

1-a

a

1-a

(16)

 

(6)

(7)

(8)

= дс	))е'^и	', где	L _ L~
= /1(С	))е*	^г. где	A A~
У	К^а	(AL)^]-«
AL~		AL	*

где у = Y/AL, к = K/AL, т. е. рассматривается выпуск и капитал на единицу эффективного труда.

у = к^и (9)

Модель Солоу предполагает, что доля капитала в доходе (а) приблизительно составляет '/з» эластичность среднедушевого до­хода по уровню сбережений равна 0,5 и эластичность по отноше­нию к темпам роста примерно равна 0,5.

Г. Мэнкью, Д. Ромер и Д. Уэйл пытаются исследовать, действи­тельно ли реальный доход выше в странах с более высоким уров­нем сбережении и ниже с более высоким значением (п + g + б). Они предполагают, что:

1пЛ(0) = а + е, (17)

где а — const, a e отражает специфику анализируемых стран (country-specific shock). Логарифм подушевого дохода в данное время (=0) для упрощения равен:

 

⁶ Mankiw G., Romer D., Weil D. A Contribution to the Empirics of Economic Growth//Quarterly Journal of Economics. 1992. Vol. 107 (2). P. 407-437

In

L-oc

1 у ч

ln(s)-

A

(18)

 

Авторы предполагают также, что s и п независимы от е. Эта предпосылка позволяет нам использовать для оценки (18) метод наименьших квадратов (МНК).

Они используют данные о реальном доходе, государственном и частном потреблении, инвестициях по 195 странам в период 1960— 1985 гг. При этом п измеряется как средние темпы роста населения

Таблица 53

Оценка классической модели Солоу

(зависимая переменная: log GDP на одного человека в трудоспособном возрасте в 1985 г.)

 

 

	(	Страны
не относящиеся к нефтедобывающим	со средним уровнем развития	ОЭСР
Количество наблюдений
CONSTANT	5.48 (1.59)	5.36 (1.55)	7.97 (2,48)
In U/С DP)	1.42 (0.14)	1.31 (0.17)	0,50 (0,43)
In (п + ц + б)	-1.97 (0.56)	-2.01 (0.53)	-0.76 (0.84)
R^2	0.59	0.59	0.01
s.e.e.	0.69	0,61	0.38
Сокращенная регрессия:
CONSTANT	6.87 (0.12)	7.10 (0.15)	8.62 (0.53)
\n{l/GDF) - ln(w + g+ 6)	1,48(0.12)	1.43 (0.14)	0.56 (0.36)
R^2	0.59	0.59	0.06
s.e.e.	0,69	0.61	0.37
Проверка ограничений (Test of restriction):
/>—сшгистикя	0.38	0.26	0.79
Предполагаемое значение а	0.60 (0.02)	0.59 (0.02)	0,36 (0.15)

В скобках указана стандартная ошибка. Темп роста инвестиций и населе­ния дан в среднем за период 1960-1985 гг. Темп роста (g + б) предполагается равным 0,05

Источник: Mankiw С, Romer D.. Weil D. A Contribution to the Empirics of Economic Growth//Quarterly Journal of Economics. 1992. Vol. 107 (2). P. 414.

в трудоспособном возрасте (15—64 года), s — как средняя доля реальных инвестиций (включая государственные) в реальном ВВП, a Y/L —как реальный ВВП в 1985 г., деленный на население в трудоспособном возрасте в том же году. Все страны разделяются на три группы. В первую включаются 98 стран, не относящихся к нефтедобывающим, do вторую — 75 стран со средним уровнем развития и в третью — 22 страны ОЭСР. Авторы исходят из того, что g + 5 = 0,05.

Результаты эмпирического анализа представлены в табл. 5.3. Они в целом подтверждают классическую модель Солоу прежде всего потому, что: 1) коэффициенты сбережений и темпов роста насе­ления в двух выборках из трех подтверждают предполагаемую связь и статистически значимы; 2) коэффициенты при In (s) и при In (n + g + 6) примерно равны по величине и противоположны по чнаку, т. е. нельзя отвергнуть гипотезу о равенстве нулю их суммы; 3) различия в сбережениях и темпах роста населения для большин­ства стран объясняются различиями в доходе на душу населения. Однако нельзя сказать, что эта эмпирическая проверка нас может полностью удовлетворить. В частности, оценка влияния сбережений и темпов роста трудоспособного населения получилась гораздо большей, чем предполагалось моделью. К тому же ос (показывающая долю капитала в доходе) оказалась равной 0,60 (при стандартной ошибке 0,02), а не 0,30—0,35, как теоретически предполагалось. Поэтому авторы идут по пути расширения модели путем включения в нее человеческого капитала.