При небольшом числе наблюдений (менее 25) основное уклонение следует определять по формуле

где сумма квадратических уклонений от М, умноженных на частоту, делится на количество наблюдений без единицы (n—1).

В этой формуле выражение Σpα² не может приниматься тождественным выражению Σра², где а² есть уклонение от А (от приближенной средней).

Отыщем σ при n =15:

Число жаберных тычинок 29 30 31 32 33 34 35 36 37 n

Частота 1 1 2 5 2 2 0 0 2 15

Так как здесь принимаются отклонения от М, то необходимо сначала определить М. М =32,60.

Находим уклонения от нашего М, т. е. от 32,60.

Если бы вычисления шли при неуменьшенном n, т. е. при 15, ii не при 14 (n—1), то σ равнялась бы ±2,15. Различие сигм для малого п (15) существенно.

При работах по определению морфологических признаков рыб вообще не следует вести вариационно-статистическую обработку при малом количестве особей (менее 25), апотому и пользоваться рассмотренной формулой ( ) почти

не приходится. Если же приходится, то во всяком случае не следует вычисления сигмы вести таким длительным способом, какой мы только что рассмотрели, а решать способом уклонений или способом сумм.

К решению формулы можно придти, пользуясьформулой

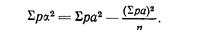
Решение ряда можно вести так

Ход решения данного примера можно вести и иначе. Составляем решетку.

Решение идет таким образом

Отсюда

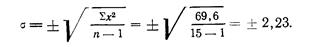
В рядах, где классовый промежуток не единица, найденное значение сигмы нужно помножить на величину классового промежутка (λ):

Коэффициент вариации С и средние ошибки М, σ и С

Сигма определяет степень варьирования признака, степень изменчивости вариационного ряда, но при сравнении двух признаков, у которых М различно, сравнение сигм не создает правильного представления об изменчивости данных признаков. Предположим, что в одном случае σ =±1,25, М=20,68; в другом случае σ=±2, а М=38. Какой признак наиболее изменчив?

Если бы средние были приблизительно одинаковы, мы могли бы сказать, что ряд с σ = ±2 более протяженный и значит более изменчивый. Но при различных средних может оказаться, что ряд с сигмой, равной ±1,25, более изменчив.

Чтобы сравнить изменчивость этих двух рядов, нужно сигму выразить в процентном отношении к средней величине того же ряда, к которому относится сигма. Это процентное отношение σ к М и называется коэффициентом вариации. Коэффициент вариации обозначаем буквой С.

В нашем примере σ = 1,25.

В другом случае (при σ=±2):

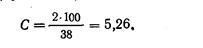
Таким образом, ряд с большой сигмой оказался менее изменчив, чем ряд с сигмой, равной ±1,25. При помощи С мы можем сравнивать любые признаки, например вес рыбы и ее размер, выраженные в любых единицах измерения, так как С есть величина отвлеченная (процент от М). Таким образом, коэффициент вариации является мерилом относительной степени изменчивости определенного признака.

Средние ошибки М, σ и С

Необходимо указать на способы нахождения средних ошибок: средней величины (М), основного уклонения (σ), коэффициента вариации (С) и разности средних величин (M₁—М₂). Формулы ошибок первых трех величин очень просты и не требуют никаких пояснений.

Средняя ошибка М или В тексте среднюю ошибку можно обозначить ±m и ставить рядом с той величиной, к которой она относится: М±т, σ±т (для краткости пишут М_m, σ_т и т. д.).

Средняя ошибка показывает возможное колебание средней М. В нашем примере средняя величина получилась равной 20,68%. В другом случае при подобных же измерениях длины хвостового стебля воблы М может получиться иное. Предел колебания средней и определяется формулой

В данном примере

или, округляя до сотых, т_м= ±0,13,

Т. е. М может быть более или менее 20,68 на 0,13.

Ошибка средней, как видно из формулы, зависит от количества наблюдений: чем больше число измеренных особей, тем ошибка меньше; она обратно пропорциональна корню квадрат ному из числа измерений. Значит, от нее зависит величина ошибки. Полученная нами величина вместе с ее средней ошибкой должна быть записана так: М ± m = 20,68 ± 0,125

Или короче

М_m=20,68 ±0,125.

Средняя ошибка квадратического уклонения находится по формуле

В наших работах этой ошибке обычно придается малое значение, равно как и ошибке коэффициента вариации, которая высчитывается по формуле

Значение ошибки квадратического уклонения и ошибки коэффициента вариации то же, что и ошибки М, т. е. т определяет колебание величин, к которым ошибка относится.

Дифференция рядов

Наибольшее значение при ихтиологических работах имеет средняя ошибка разности средних величин признаков двух групп рыб. При установлении вида, подвида, расы и морфы необходимо пользоваться формулой дифференции или расхождения рядов. Многие авторы в своих статьях называют эту формулу diff. (сокращенное слово differentia):

где M₁—М₂— разность средних величин взятых рядов, а —средняя ошибка этой разности. Из выражения видим, что средняя ошибка разности средних величин равна квадратному корню из суммы квадратов средних ошибок, соответствующих данным средним величинам: т²₁ — квадрат средней ошибки M₁, a m²₂ — квадрат средней ошибки M₂.