Можно находить среднее арифметическое, пользуясь способом сумм. При этом умножение частот на уклонения заменяется сложением частот. Найдем среднюю длины хвостового стебля воблы ряда и этим способом.

Выпишем частоты нашего ряда, начиная с частоты, соответствующей наибольшей варианте ряда, в виде вертикального столбца. За А мы примем, как и ранее, середину класса 20,5 — 21,5, т. е. 21,05. Для ясности частоту 38, соответствующую нашему А, включим в рамку

Приготовим рядом с нашим столбцом место еще для двух новых столбцов и разместим в этих добавочных столбцах четыре черточки следующим образом: две против частоты 38 в обоих столбцах и две во втором столбце против частот, соседних 38:

Теперь рядом с верхней и нижней частотами напишем их еще раз (в обоих столбцах):

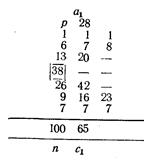
Затем заполняем два новых столбца (т. е. второй и третий) следующим образом: к верхней частоте прибавляем следующую частоту левого столбца и пишем полученную сумму, в данном случае 1+ 6 = 7, в столбце под первой частотой к этой сумме (к 7) прибавляем следующую частоту (13) и т. д. до черточки. Затем то же делаем и с нижней частью столбца (начинаем снизу: 7 + 9 = 16; 16 +26 = 42). Таким образом заполняем второй столбец:

Заполнив второй столбец, таким же образом заполняем и третий столбец, доходя сверху и снизу до черточек (в данном случае приходится находить по одной сумме):

Составив новые столбцы, приступаем к их суммированию; причем сумму верхней части и сумму нижней части второго столбца можно получить, сложив цифры над черточками в верхней части и под черточками—в нижней в обоих новых столбцах. Сумма верхней части 20+8=28(1+7+20=28); сумма нижней части: 42+23=65(42+16+7=65). Эти суммы записаны над столбцом и под столбцом и обозначены а₁ и с₁. Теперь из суммы верхней части столбца (из 28) вычтем сумму нижней части столбца (65) и получим величину 37, соответствующую ∑ра (см. выше). Обозначим эту величину здесь через S₁:

S₁ = a1— c1 = 28 — 65 = — 37.

Дальнейший ход решения такой же, как и при способе уклонении, а именно:

Теперь остается отыскать М

М=А + b₁ =21,05 + (—0,37) =20,68%.

Получилась величина М такая же, как и при решении способом уклонений. Если решение ряда ограничивается отысканием одной средней М, можно второй новый столбец не заполнять, а суммы верхней и нижней части первого (добавочного) Столбца находить непосредственно из этого столбца.

Средняя арифметическая (М), несомненно, с большей, чем мода, точностью определяет среднюю величину вариационного ряда, т. е. среднее качество признака. Средняя характеризует типичность взятого признака.

В приведенном примере размах варьирования длины хвоста воблы выразился от 18 до 24 (в процентах длины тела), но мы не можем сказать, что эти числа обязательны для любого количества взятых для исследования особей: возьмем меньшее количество рыб — ширина нашего ряда, возможно, сократится, возьмем большее — ряд может расшириться; кроме того, не исключается возможность, что крайние члены этого ряда относятся не к этому, а к другому ряду, т. е. рыбы, которым свойственны крайние величины ряда, входят в другую систематическую группу.

Таким образом, средняя величина не характеризует ни ширину вариационного ряда, ни размах варьирования.

Среднее квадратическое или основное уклонение σ. Нахождение σ способом уклонения и способом сумм

Наилучшей мерой определения размаха или протяженности Вариационного ряда или степени варьирования того или другого Признака в настоящее время считается основное или среднее квадратическое уклонение, обозначаемое буквой σ. (сигма). Для получения этой величины уклонения вариант от средней величины (М), обозначаемые нами буквой а, возводятся в квадрат, перемножаются на их частоты, произведения суммируются, сумма делится на общее число случаев (особей) и из полученного числа извлекается квадратный корень, т. е.

По этой формуле сигму (о) определяют редко, вычисление среднего квадратического уклонения ведут теми же непрямыми способами, как и среднего арифметического, т. е. по уклонениям от А и способом сумм.

Способ уклонений

σ = √b₂ – b₁²

Пользуемся тем же примером (стр.301), но здесь уклонения а² берутся в квадрате: 1, 4, 9,.....

Числа случаев, уклоняющихся и влево от А, здесь должны иметь также знак плюс, потому что отрицательное уклонение (—а), будучи возведенным в квадрат, становится величиною положительной.

Уклонения (а²) 1 4 9

Частота уклонений (р) +26 +9+7

+13 +6 +1

Алгебраическая сумма частот

уклонений (∑p) +39 +15 +8

Сумма квадратических уклонений от А, помноженных на частоту

(∑ pa²): 39 + 60 + 72 = 171,

Возведение в квадрат и извлечение корней квадратных можно вести по специальным таблицам.

Уклонения в квадрате
+60
Простые уклонения
Частоты	-
+					100 1,71 b2 = 1.71
Вычисление b1	-13 – 6 – 18 = - 37/ 100 = - 0.37

При пользовании способом уклонений запись вычисленных величин можно упростить следующим образом. Записав уклонения и частоты обычным порядком (причем плюс и минус не нужно повторять, а ставить их один раз слева от частот) и, высчитав b₁. записываем над простыми уклонениями уклонения в квадрате. Далее проводим справа вертикальную черту и за чертой записываем в виде столбца произведения сумм частот на уклонения в квадрате, помня, что частоты здесь будут со знаком + (плюс). Данные произведения складываем, делим на п. и получаем значение b₂. При такой записи достигается большая экономия времени.

Способ сумм

σ = ±

Пользуемся тем же примером, какой приведен для вычисления средней.

Ci

Σx² (в формуле) означает сумму центральных уклонений (т. е. уклонений от M), равную ; S₁ уже найдено (—37), возведем его в квадрат и, разделив на п, получим

Находим S₂ S₂ = a₁ + с₁ + 2(а₂ + с₂)

а₁ и с₁ нам известны (a₁=28, с₁=65; это—суммы верхней и нижней частей второго столбца); а₂ — сумма верхней части третьего столбца (8+1=9); с₂—сумма нижней части третьего столбца (23+7=30). Таким образом, в числовых выражениях:

S₂ = 28 + 65 + 2 (9 + 30) = 93 + 78 = 171.

Σx²= 171— 13,69 = 157,31.

Для определения о найденное значение Σx² делим на n и из полученного частного извлекаем квадратный корень:

Можно рекомендовать пользоваться при вычислении сигмы комбинированным способом, т. е. соединением обоих способов (способа уклонений и способа сумм). Поясним на примере: Находим S₁и S₂ (по способу сумм), которые по величине всегда будут равны Σ ра и Σ ра². После этого можно перейти к нахождению b₁ и b₂ (по способу уклонений) и, наконец, по формуле σ=± находим сигму, т. е. среднее квадратическое уклонение:

Практическое значение найденных нами величин: М=20,68 и σ =±1,25 таково.

Типичная величина процентного отношения длины хвостового стебля воблы к длине тела равна 20,68%. Чтобы знать, насколько данная форма в этом признаке уклонилась от средней, типичной, формы, нужно знать протяженность вариационного ряда. Если, например, ряд короткий, то и небольшие отклонения от средней будут иметь большее значение, чем такие же отклонения более протяженного ряда. Сигма и показывает протяженность данного вариационного ряда. Чем меньше σ, тем ряд менее изменчив, т. е. протяженность его меньше. Но математически доказано, что 1σ не может гарантировать протяженность ряда во всех случаях. Поэтому берут не 1σ, а З σ и даже 3,5σ.

При нормальном распределении вариант, идеальным случаем которого является распределение коэффициентов двучлена (бинома), возведенного в какую-либо высокую степень, приближающуюся к бесконечности, вариационный ряд и его графическое изображение — нормальная вариационная кривая имеет строго симметричное построение и в таком ряду в промежутке:

от М до ± 1σ укладывается около 68% случаев

» М» ±2σ »» 95,5%»

» М» ±3 σ»» 99,7%»

» М» ±3,5 σ»» 99,95%»

Иначе говоря, более чем на 3σ могут уклониться из 100 случаев только три случая. Поэтому, зная одну, две и три сигмы, мы можем определить возможную протяженность нашего конкретного вариационного ряда, следующего закономерности нормального распределения, т. е. можно узнать его крайние варианты. Обратимся к нашему примеру.

Класс: 17,5—18,5—19,5—20,5—21,5—22,5—23,5—24,5 n

Частота 7 9 26 38 13 6 1 100

M=20,68 σ=±l,25 3 σ=±3,75

Следовательно, крайние члены ряда, если основываться на 3σ, должны быть 16,93 (20,68—3,75) и 24,43 (20,68+3,75), т. е. наш первый эмпирический ряд меньше второго теоретического, а это говорит о том, что мы можем встретить воблу, длина хвостового стебля которой может быть меньше той величины, какую мы наблюдали, т. е. не 18, а 17%, но правая сторона ряда и теоретически не превосходит 24%, т. е. с более длинным хвостовым стеблем воблу едва ли встретим. Для большей осторожности лучше брать не 3, а 3,5σ. Рассчитав протяженность ряда по 3,5σ, получим 16,30—25,06; при таком расчислении можно предполагать три новых варианта (16, 17 и 25%).