Описание математической модели для участка линейной конфигурации
В основу математической модели положен принцип использования матрицы корреспондирующих вагонопотоков и разбиение этой матрицы на матрицы корреспонденций отдельных поездов, - в отличие от стандартно используемого поструйного разбиения множества корреспондируемых вагонов. Для оптимизации вариантов организации вагонопотока, в роли которых выступают множества матриц корреспонденций, выбирается ряд критериев.
Метод оптимизации, сходный по принципу применения с методом динамического программирования получил название " метод повышения размерности ". Он состоит в поиске оптимальных вариантов в классе вариантов с фиксированным числом поездов, при последовательном увеличении их числа до тех пор, пока возможно улучшение какого - либо из критериев.
Для описания модели будем опираться на наиболее простые объекты и критерии. А именно, рассмотрим наипростейшую линейную конфигурацию полигона железных дорог (рис. 1.5.1). При этом схема модели существенно не изменится для линейного полигона большей протяженности (рис. 1.5.2).
В качестве основных исходных данных примем величины вагонопотока "от станции к станции" ki,j (i ³ 1, j £ N), где N - число станций, принадлежащих рассматриваемому полигону, представленные матрицей корреспонденций вагонопотока K = ki,j. В случае N = 3 эта матрица имеет вид:

Каждая величина составлена из трех компонентов:

где  - число груженых вагонов под выгрузку на станцию j со станции i, - число груженых вагонов под выгрузку на станцию j со станции i,
 - число порожних вагонов под погрузку на станцию j со станции i, - число порожних вагонов под погрузку на станцию j со станции i,
 - число груженых вагонов на станцию j со станции i, попадающих под сдвоенные операции на станции j. - число груженых вагонов на станцию j со станции i, попадающих под сдвоенные операции на станции j.
В зависимости от операций, производимых на конечном пункте, соответственно и  .Число вагонов, следующих без переработки, на станции В учитывается иначе. А именно, величины .Число вагонов, следующих без переработки, на станции В учитывается иначе. А именно, величины  и и  равны, соответственно, количествам вагонов, следующих из A в B и из В в С, в то время как величина равны, соответственно, количествам вагонов, следующих из A в B и из В в С, в то время как величина  складывается из числа вагонов, следующих в прямых поездах из А в С, и из числа вагонов, следующих из А в С без переработки в В в поездах, останавливающихся в В: складывается из числа вагонов, следующих в прямых поездах из А в С, и из числа вагонов, следующих из А в С без переработки в В в поездах, останавливающихся в В:
k 12= k AB, k 23= k BC, k 13= k AC+ k ACB.
Kаждый вариант организации вагонопотоков - точку в пространстве поиска - будем представлять множеством  , ,
где n - число поездов.
Каждому поезду соответствует матрица  корреспонденций вагонопотока i - го поезда. Эта матрица является верхнетреугольной или нижнетреугольной в зависимости от направления движения (четное или нечетное): корреспонденций вагонопотока i - го поезда. Эта матрица является верхнетреугольной или нижнетреугольной в зависимости от направления движения (четное или нечетное):

На коэффициенты матрицы  (аналогично и для (аналогично и для  ) накладываются следующие ограничения: ) накладываются следующие ограничения:
 , ,  
где  - максимально возможное число вагонов в составе поезда на участке i - j. - максимально возможное число вагонов в составе поезда на участке i - j.
Реальное число вагонов в поезде может варьироваться: оно равно  на участке А - В и на участке А - В и  на участке В - С. на участке В - С.
В соответствии с вышесказанным можно записать для каждого участка i - j

На практике следует учитывать также 3 компонента матриц V:
  , ,  . .
С помощью матрицы V формируется матрица поездопотока Р, включающая число поездов в четном (+) направлении (выше диагонали) и нечетном (-) направлении (ниже диагонали):
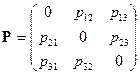 . .
Коэффициенты матрицы P должны удовлетворять условию по ограничению пропускной способности участка:
 , ,
где  - число грузовых поездов, следующих по участку i - j, - число грузовых поездов, следующих по участку i - j,
 -общее число всех иных поездов, предусмотренных графиком движения на участке i - j, -общее число всех иных поездов, предусмотренных графиком движения на участке i - j,
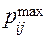 -пропускная способность участка i - j. -пропускная способность участка i - j.
|