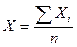К общенаучным методам анализа относят индукцию и дедукцию, абстрагирование и системный анализ, моделирование, синтез и друб.

Среди общих методов познания наиболее распространенными являются индукция и дедукция, их природа сугубо диалектична; они неразрывно связаны между собой. Индукция, не опирающаяся на общую теорию, может лишь упорядочить факты, но не открыть законы, внутренне присущие познанию. Дедукция сама по себе, без индукции имела бы схоластический характере. Но она становится мощным средством познания, если обосновывается фактами. Диалектическая взаимосвязь индукции и дедукции в процессе познания означает обобщение опыта, фактов должно основываться на наиболее общих положениях, общих законах.

Использование диалектического метода в экономическом анализе означает, что каждый процесс, явление надо рассматривать как систему, как совокупность многих элементов, связанных между собой. Из этого вытекает необходимость системного подхода к изучению объектов анализа, что является еще одной его характерной чертой.

Главные особенности системного подхода – это динамичность, взаимодействие, взаимозависимость и взаимосвязь элементов системы, комплексность, целостность, соподчиненность, выделение ведущего звена. Системный подход предусматривает максимальную детализацию изучаемых явлений и процессов на элементы (собственно анализ), их систематизацию и синтез.

Специальные методы представлены двумя группами – экономико-логические и экономико-математические. Методические приемы данной группы просты и доступны для практического применения.

Важнейшими методами обработки экономической информации, применяемыми при анализе экономики, являются экономико-логические - сравнение, абсолютные и относительные величины, средние величины, индексы, элиминирование, сводка и группировка, балансовый и метод прямого счета и друб.

Методы сравнения.

Сравнение - присуще каждому экономическому расчету. Сравнение это метод анализа, позволяющий выявить взаимосвязь экономических явлений, их развитие и степень достижения эффективности в использовании материальных, трудовых и финансовых ресурсов, путем выражения характеристик явлений через другие однородные явления.

Использование приема сравнения предполагает сопоставимость сравниваемых показателей: единство оценки, сравниваемость календарных сроков, устранение влияния различий в объеме и ассортименте в отдельных случаях, сезонных особенностей и территориальных различий, географических условий, различий в методике расчета показателей и т.д.

Различают следующие основные виды сравнений (рис.3.2):

 

 

Рисунок 3.2 – Виды сравнительного анализа

 

Сравнение отчетных показателей с плановыми - позволяет выявить причины невыполнения плановых заданий по отдельным показателям и наметить мероприятия для улучшения работы предприятия в дальнейшем;

Сравнение отчетных показателей с показателями предшествующих периодов - показывает темпы роста производства, динамику показателей, тенденцию развития предприятия; межхозяйственные сравнения,

Сравнение показателей предприятия с показателями других предприятий, - позволяет вскрыть многие резервы, перенять передовой опытыс.

Межхозяйственные сравнения конкурентов получили в экономическом анализе широкое распространение и практически выделились в самостоятельный вид анализа - так называемый межхозяйственный сравнительный анализ. В условиях рыночной экономики сравнительный анализ работы предприятий-конкурентов является объективной необходимостью для повышения эффективности и выживаемости в конкурентной борьбе. Можно проводить сравнение не только родственных предприятий. Финансовые коэффициенты, взятые во всеобщей денежной оценке, позволяют найти общий знаменатель для сравнения качества работы предприятий разных отраслей:

Сравнение со среднеотраслевыми данными - позволяет определить, соответствуют ли индивидуальные затраты на данном предприятии общественно необходимым, установить организационно-технический уровень предприятия и место, занимаемое им в ряду других предприятий данной отрасли; сравнение показателей предприятия со средними показателями рыночной экономики в основном в форме финансовых коэффициентов.

Перечисленные виды сравнения являются основными, но при изучении экономики используется много других видов сравнений.

Для аналитических процедур в сравнении широко применяются абсолютные, относительные и средние величины.

Абсолютные и относительные величины. С помощью абсолютных величин характеризуются размеры (уровни, объемы) экономических явлений и показателей. Относительные величины используются для характеристики степени выполнения планов, измерения темпов (относительной скорости) развития производства и т.д. Особой формой относительных величин являются проценты, при которых базисная величина принимается не за 1, а за 100. Относительные величины иногда выражаются в промилле, когда базисная величина принимается за 1000. Относительные величины могут быть выражены в разной форме:

1) В виде коэффициента–база сравнения равна 1,

2) В виде процента–база сравнения равна 100,

3) В виде промиле–база сравнения равна 1000,

4) В виде децимиле–база сравнения равна 10000.

В каждом отдельном случае надо выбрать такую форму относительной величины, которая выразила бы интересующее нас соотношение с наибольшей наглядностью.

Средние величины. Для обобщающей характеристики массовых, качественно однородных экономических явлений пользуются средними величинами, способы расчета которых различны.

Средние величины–это обобщенная количественная характеристика качественной однородной массы общественных явлений, всегда получаемая расчетным путем. Рассчитываются средние величины в аналитической работе за отчетные периоды – месяц, квартал, год.

Средняя величина выражает собой отличительную особенность данной совокупности явлений, устанавливает ее наиболее типичные черты. Применяют различные формы средней величины:

– Средняя арифметическая,

– Средняя гармоническая,

– Средняя геометрическая,

– Средняя хронологическая моментного ряда,

– Мода и медиана.

Средние величины делят на степенные (простые и взвешенные) и структурные. Степенная средняя, в зависимости от степени «Z», может представлять собой различные виды средних величин.

При «Z»= - 1 получаем среднюю гармоническую (х_h)

где х_i – количественное значение признака каждой единицы совокупности;n – число единиц совокупности.

При «Z»= 0 получаем среднюю геометрическую (х_г):

При «Z»=+1 получаем среднюю арифметическую (х_а):

При «Z»=+2 получаем среднюю квадратическую (х_кв):

При «Z»=+3 получаем среднюю кубическую (х_куб):

Если варианты встречаются неодинаковое число раз, то средние величины рассчитываются не как простые, а взвешенные по следующим формулам:

Средняя гармоническая взвешенная (х_hв)

 

где fi - частота вариантов; xi- варианты осредненного признака,

Средняя геометрическая взвешенная (x_qв):

Средняя арифметическая взвешенная (х_ав):

Средняя квадратическая взвешенная (х_квв):

–

Мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном ряду. Медиана (Ме) соответствует варианту, занимающего середину ранжированного ряда.

Расположение медианы определяется ее номером (Nме), который рассчитывается по формуле:

 

Медианная строка в вариационной таблице определяется по накопленной частоте Si, численная величина которой должна быть равна или на немного больше медианы.

Численное значение самой медианы определяется по формуле:

 

Где х_ме – нижнее значение медианного интервала;

h – величина медианного интервала;

S_ме-1 – накопленная частота, предшествующая медианному интервалу

fме – частота (частость, вес) медианного интервала.

Медиану можно определить и по графику. Для этого по накопленным частотам S вычерчивается кумулята и из точки на оси ординат, соответствующей номеру медианы, проводится прямая параллельно оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс будет указывать на численное значение медианы (рис.5).

Модой (Мо) называют часто встречающееся значение признака у исследуемых единиц совокупности. Мода в вариационном ряду с равными интервалами определяется по формуле:

 

Ряды динамики. Рядом динамики называется ряд данных, характеризующих изменение явления, показателей во времени. Каждое отдельное значение показателя ряда динамики называется уровнем. Для характеристики изменения уровня ряда динамики исчисляют абсолютный прирост и темп роста и прироста.

Темп роста дает характеристику степени изменения уровня продажи продукции от одного года к другому. Для получения общей характеристики темпа изменения уровня продукции за весь период исчисляют средний темп. Характеристикой среднего темпа служит средняя геометрическая из темпов. Для расчета среднего темпа роста и прироста динамического ряда применяется логарифмирование.

 

Рисунок 3.3 – Основные способы эллиминирования

Метод элиминирования

В экономическом анализе используются обобщающие показатели хозяйственной деятельности, на которые влияют различные факторы - как основные, так и побочные, вне­шние.