
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет основных типов фрикционных узловСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчетный момент Исходным условием для расчета блокировочных муфт и опорных тормозов коробок передач является величина номинального момента Мн, который должен передавать фрикцион. Расчетный момент определяется на основании анализа кинематической схемы трансмиссии при условии, что двигатель развивает максимальный момент. Для надежной работы фрикцион должен быть рассчитан на момент, превышающий расчетный: МФ=βMН, (56) Очевидно, что включение фрикциона может произойти лишь в том случае, когда минимальное значение коэффициента запаса больше единицы. При этом во включенном фрикционе запас по моменту будет автоматически обеспечен. При расчете фрикционов механизма поворота поступают аналогичным образом с той лишь разницей, что номинальный момент определяется исходя из наибольшей силы тяги забегающей гусеницы по сцеплению с грунтом. Для определения расчетного момента остановочного тормоза рассмотрим два характерных режима его работы: удержание машины на спуске и торможение на горизонтальном участке. В первом случае при максимальном угле подъема αтах тормозная сила должна отвечать условию
Если тормоз установлен между механизмом поворота и бортредуктором, как это обычно и делается, то тормозной момент, необходимый для удержания машины,
Здесь G – вес гусеничной машины; rвк – радиус ведущей звездочки; iбр – передаточное число бортредуктора; ηбр – к.п.д. бортредуктора; ηг – к.п.д. гусеничного движителя. Максимальный угол αтах может быть определен из условия сцепления гусениц с грунтом. Для торможения машины на горизонтальном участке при полном использовании сил сцепления гусениц с грунтом тормозной момент должен быть
Расчет дисковых фрикционов Рассмотрим расчетную схему фрикционного узла (рис. 100). Диски трения сжимаются силой Р, которая создается пружинами во фрикционах с механическим приводом включения или поршнем бустера во фрикционах с гидроприводом. Момент с ведущих деталей на ведомые передается за счет сил трения между сжатыми дисками. Удельное давление на диски будем считать равномерно распределенным по всей поверхности трения, т.е.
Часто для определения момента фрикциона пользуются упрощенной формулой
Рис. 100 Расчетная схема фрикционного узла Расчет ленточных тормозов Рассмотрим равновесие элементарного участка тормозной ленты (рис. 101). На концах участка действуют силы натяжения S и S+dS. Приращение натяжения обеспечивается силой трения
Проектируя все действующие силы на направление dN и пренебрегая бесконечно малыми величинами высших порядков, имеем
Интегрируя полученное уравнение в пределах
откуда
Рис. 101. Схема Рис. 102. К расчету ленточного тормоза ленточного тормоза Определим создаваемый тормозом момент при условии, что один конец тормозной ленты жестко закреплен, а ко второму приложена сила S0 (рис. 102). Силу, действующую на закрепленном конце ленты, находим по формуле (67):
Из условия равновесия ленты, на которую действует тормозной момент Мт и натяжение концов S0 и S1, имеем
При вращении барабана в сторону, противоположную указанной на рисунке,
Сравнивая правые части формул (69) и (71), находим, что во втором случае тормозной момент в еma раз меньше, чем в первом. Таким образом, ленточный тормоз с одним закрепленным концом ленты может эффективно работать при вращении барабана лишь в одном направлении. В этом случае реализуется эффект самозатягивания.
При затяжке ленточного тормоза равнодействующая сил S0 и S1 действует на барабан, вызывая изгибные напряжения в валу и нагружая его опоры. Геометрическое сложение сил S0 и S1 дает
Из этой формулы следует, что радиальная нагрузка Рр минимальна при
Так, при α=5 рад и δ=2,5 мм h= 12,5 мм. С учетом износа ход свободного конца ленты должен составлять 15-18 мм. При проектировании ленточного тормоза радиус тормозного барабана и угол охвата определяются обычно конструктивными соображениями. Ширина ленты В находится из условия обеспечения требуемого удельного давления qmах. Для его определения поделим обе части выражения
Учитывая, что
Отсюда видно, что удельное давление возрастает от одного конца ленты к другому против направления вращения барабана (рис. 102). Максимальное значение его
Таким образом, требуемая ширина ленты
Как было отмечено выше, тормоз с одним закрепленным концом может эффективно работать лишь при одном направлении вращения тормозного барабана. Этот недостаток устраняется применением плавающего закрепления концов ленты. В зависимости от направления вращения тормозного барабана пальцы, имеющиеся на обоих концах ленты, упираются в кронштейн, и соответствующий конец тормозной ленты становится неподвижным. Таким образом, эффект самозатягивания реализуется в таком тормозе при любом направлении вращения барабана. Помимо упомянутых двух схем закрепления концов тормозной ленты применяются и другие, например с обоими подвижными концами, двойной тормоз. Во всех этих случаях расчет ленточного тормозного механизма может производиться по изложенной выше методике.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.21.234 (0.01 с.) |

 (57)
(57) . (58)
. (58) (59)
(59)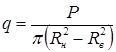 , (60)
, (60) , (61)
, (61) . (62)
. (62)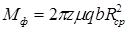 , (63)
, (63) . (64)
. (64)
 (65)
(65) , или
, или . (66)
. (66)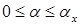 , и
, и 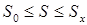 , где aх, и Sх – текущие значения угла и натяжения, получаем
, где aх, и Sх – текущие значения угла и натяжения, получаем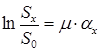 ,
, . (67)
. (67)
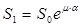 . (68)
. (68) . (69)
. (69)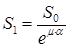 , (70)
, (70)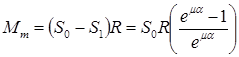 . (71)
. (71) (72)
(72) . Поэтому при конструировании тормоза нужно стремиться к тому, чтобы угол охвата барабана лентой был максимальным. Для того чтобы тормозная лента не терлась о барабан в выключенном положении, между лентой и барабаном должен быть зазор d=2-2,5 мм. Для обеспечения зазора устанавливаются пружины, оттягивающие в нескольких местах ленту. При затяжке тормоза этот зазор выбирается. Таким образом, перемещение свободного конца ленты
. Поэтому при конструировании тормоза нужно стремиться к тому, чтобы угол охвата барабана лентой был максимальным. Для того чтобы тормозная лента не терлась о барабан в выключенном положении, между лентой и барабаном должен быть зазор d=2-2,5 мм. Для обеспечения зазора устанавливаются пружины, оттягивающие в нескольких местах ленту. При затяжке тормоза этот зазор выбирается. Таким образом, перемещение свободного конца ленты . (73)
. (73) . (74)
. (74)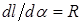 , получим
, получим . (75)
. (75) . (76)
. (76)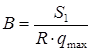 . (77)
. (77)


