
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Звичайна практика визначення номінальної процентної ставки позичкового капіталуСодержание книги
Поиск на нашем сайте
На прикладі казначейських облігацій США. Ці облігації згідно статуту забезпечують прибутковість в 6%. Якщо рівень інфляції в наступному році складе 2%, то облігації оголошуються з номінальною процентною ставкою: 6% + 2% = 8%. Додаток у 2% має назву „інфляційної премії". Наведемо більш точний виклад цього питання. Нехай інвестор очікує отримати 10 процентів на $1000 вкладених грошей, тобто $1.100 до кінця року. Якщо передбачається темп інфляції 12%, то інвестор коригує свої очікування наступним чином: $1.100 х (1+0,12) = $1.232, тобто в цілому він отримає: $1.000 х (1+0,10) х (1+0,12) = $1.232.
5.3.2. Відношення до інфляції в реальній практиці Прогнозування темпів інфляції дуже складний процес, діючий на фоні великої кількості невизначеностей. Це особливо характерно для країн з нестійким економічним станом. Окрім того, темпи інфляції в окремі періоди в значній мірі підпадають під вплив суб'єктивних факторів, що слабко піддаються прогнозуванню. Тому один із найбільш реально значущих підходів може полягати у наступному: ■ Вартість інвестованих засобів і суми грошових засобів, які забезпечують їх повернення, перераховуються із національної валюти в одну з найбільш стійких твердих валют (долар США, фунт стерлінгів Великобританії, німецькі марки). Перерахунок виконується по біржовому курсу на момент проведення розрахунків. ■ Процес нарощення і дисконтування виконується в даному випадку, не звертаючи уваги на інфляцію. ■ Конкретна процентна ставка визначається, виходячи з джерела інвестування. Наприклад, при інвестуванні за рахунок кредитів комерційного банка в якості показника дисконту приймається процентна ставка валютного кредиту цього банка. 5.4. Нарощування і дисконтування грошових потоків Оскільки процес інвестування, як правило, має велику подовженість, в практиці аналізу ефективності капітальних вкладень, зазвичай, при-ходиться мати справу не з одиничними грошовими сумами, а з потоками грошових засобів. Вирахування нарощеної і дисконтованої сум грошових засобів в цьому випадку виконується шляхом використання відповідних формул (5.1) і (5.2) для кожного елемента грошового потоку. Грошовий потік прийнято відображати на часовій лінії одним із двох способів (рис. 5.4).
Представлений на рис. грошовий потік полягає в наступному: в теперішній час виплачується (знак „мінус") $2.000; в перший і другий роки отримано $1.000, в третій - $1.500, в четвертий - знову $1.000. Елемент грошового потоку прийнято визначати CFk (від Cash Row), де k - номер періоду, за який розглядається грошовий потік. Теперішнє значення грошового потоку означено PV (від Present Value), а майбутнє значення FV (від Future Value).
Рис. 5.4. Два способи (А і В) графічної інтерпретації грошового потоку Використавши формулу (5.1), для всіх елементів грошового потоку від к до п отримаємо майбутнє значення грошового потоку:
Приклад 3. Після впровадження заходу зі зниження адміністративних витрат підприємство планує отримати економію $1000 за рік. Заощаджені гроші передбачається розмістити на депозитний рахунок (під 5% річних) з тим, щоб через 5 років накопичені гроші використати для інвестування. Яка сума виявиться на банківському рахунку підприємства? Вирішимо задачу з використанням часової лінії (рис. 5.5). Як видно з рисунка, через 5 років підприємство накопичить $5.526, які зможе інвестувати. В даному прикладі (випадку) грошовий потік складається з однакових грошових сум щорічно. Такий потік зветься ануїтетом (Annuity). Для вирахування майбутнього значення ануїтету використовується формула:
яка виходить з (5.5) при CFk = const. Розрахунок майбутнього значення одиничної суми та ануїтету може виконуватися з допомогою спеціальних фінансових таблиць; в даному випадку з використанням таблиці додатку В при г = 5%та п = 5 отримуємо множник 5,526, який відповідає результату розрахунку щодо даного прикладу.
Рис. 5.5. Розрахунок грошового потоку з однаковими елементами Дисконтування грошових потоків виконується шляхом багатократного використання формули (5.2):
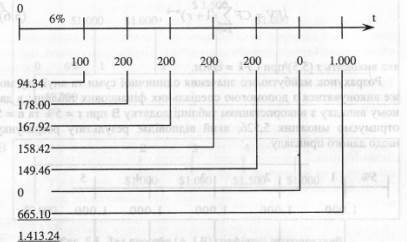
Приклад 4. Розглянемо грошовий потік з неоднаковими елементами - CF, = 100, CF2 = 200, CF3 = 200, CF4 = 200, CF5 = 200, CF6 = 0, CF7 = 1.000, для якого необхідно розрахувати поточне (сучасне) значення при показнику дисконту 6%. Рішення виконуємо за допомогою часової лінії (рис.5.6)
Рис. 5.6. Розрахунок грошового потоку з неоднаковими елементами Вирахування дисконтованих значень окремих сум можна виконувати шляхом використання спеціальних таблиць (додатки А, Б і В). Дисконтування ануїтету {CFj = const) виконується за формулою:
Для розрахунку поточного (сучасного) значення ануїтету може бути використана таблиця додатку Б. Приклад 5. Підприємство придбало облігації муніципальної позики, які принесуть йому дохід $15к=$ 15.000, хоче використати ці гроші для розвитку власного виробництва. Підприємство оцінює економічну ефективність свого вкладення отриманих грошей у 12%. Необхідно визначити поточне (теперішнє) значення цього грошового потоку. Рішення виконаємо за допомогою табл. 5.2. За результатами розрахунків ми бачимо, що: ■ дисконтоване значення грошового потоку суттєво менше арифметичної суми елементів грошового потоку; ■ чим далі ми просуваємося в часі, тим менше поточне (сучасне) значення грошей: $15.000 через рік варті зараз $13.395; $15.000 через 5 років варті зараз $8.505. Таблиця 5.2
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.195 (0.011 с.) |


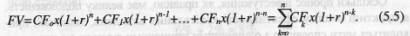
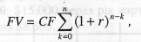 (5.6)
(5.6)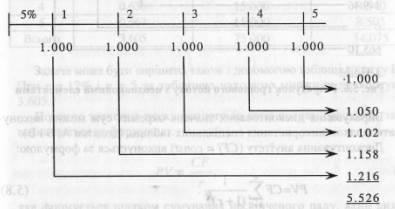
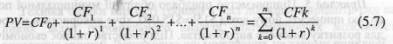
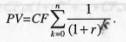 (5.8)
(5.8)


