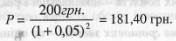Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорія грошей і перехідна економіка 5. 1.Содержание книги
Поиск на нашем сайте Концепція вартості грошей в часі
Основний принцип:
оскільки вони можуть оути інвестовані і це принесе додатковий при-буток. Цей принцип породжує концепцію оцінки вартості грошей в часі:
В якості норми прибутку виступає норма позичкового процента або норма виплати дивідендів по звичайних і привілейованих акціях. Враховуючи, що інвестування - це, зазвичай, тривалий процес, в інвестиційній практиці приходиться порівнювати вартість грошей на початку їх інвестування з вартістю грошей при їх поверненні у вигляді майбутнього прибутку. В процесі порівняння вартості грошових засобів при їх вкладанні і поверненні прийнято використовувати два основних поняття: майбутня і теперішня (сучасна) вартість грошей. їх графічна інтерпретація представлена на рис. 5.1. а) майбутня вартість грошей
б) теперішня (сучасна) вартість грошей
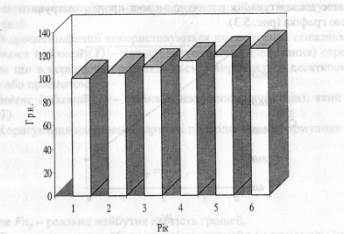
Рис. 5 .1. Графічна інтерпретація понять вартості грошей Майбутня вартість грошей - це сума інвестованих в нинішній момент грошових засобів, в які вони перетворяться через певний період часу з урахуванням певної процентної ставки. Визначення майбутньої вартості грошей пов'язане з процесом нарощення цієї вартості, який являє собою поетапне збільшення вкладеної суми шляхом приєднання до первісної її суми суми процентних платежів. В інвестиційних розрахунках процентна ставка платежів використовується не тільки як інструмент нарощення вартості грошових засобів, але і як вимірювач ступеня доходності інвестиційних операцій. Теперішня (сучасна) вартість грошей - це сума майбутніх грошових надходжень, приведених з урахуванням певної процентної ставки до теперішнього моменту. Визначення теперішньої вартості грошей пов'язано з процесом дисконтування цієї вартості, який (процес) є операцією, зворотною нарощенню. Дисконтування використовується в багатьох задачах аналізу інвестицій. Таким чином, одну і ту ж саму суму грошей можна розглядати з двох позицій: а) з позиції її сучасної вартості; б)з позиції її майбутньої вартості. Вартість грошей в майбутньому завжди вища. Елементи теорії процентів Основне поняття теорії процентів - складний процент. Складним процентом називається сума доходу, яка створюється в результаті інвестування грошей при умові, що сума нарахованого простого процента не виплачується у кінці кожного періоду, а приєднується до суми основного вкладення і в наступному платіжному періоді сама приносить доход. Основна формула теорії процентів визначає вартість грошей: Рп=Рх(1+r)x (5.1) де Р-сучасне значення вкладеної суми грошей; F- майбутнє значення вартості грошей; п - кількість періодів часу, на яку проводиться вкладання; r- норма доходності (прибутковості) від вкладення. Простішим способом цю формулу можна інтерпретувати як визначення величини депозитного вкладу в банк при депозитній ставці (в частках одиниці). Суть процесу нарощення грошей не змінюється, якщо гроші вкладаються в будь-який бізнес (підприємство). Головне - щоб вкладення грошей забезпечувало доход, тобто збільшення вкладеної суми. Приклад 1. Банк виплачує 5 процентів річних по депозитному вкладу. Відповідно до формули (5.1) 100 грн., що вкладені зараз, через рік будуть: F1 = 100 грн. х (1+0,05) = 105 грн. Якщо вкладник вирішує залишити всю суму на депозиті ще на один рік, то в кінці другого року обсяг його вкладу складе: F2 =Р х (1 +г) = 105 грн. х (1+0,05) = 110,25 грн. або за формулою (5.1): F2 = Р х (1 +г)2 = 100 грн. х (1+0,05)2= 110,25 грн. Процес нарощення вартості 100 грн. за роками можна показати у вигляді табл. 5.1 та діаграми (рис. 5.2). Таблиця 5.1 Процес нарощення вартості грошей
Рис. 5.2. Динаміка нарощення вартості грошей Теперішнє (сучасне) значення вартості майбутньої суми грошей визначається за допомогою формули:
Приклад 2. Нехай інвестор хоче одержати 200 грн. через 2 роки. Яку суму він повинен покласти на терміновий депозит зараз, якщо депозитна процентна ставка складає 5%?
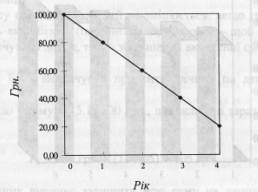
Формула (5.2) забезпечує процес дисконтування. І в цьому випадку величина г інтерпретується як ставка дисконту і часто називається просто дисконтом. Розглянутий на прикладі 2 випадок можна інтерпретувати наступним чином: 181,40 грн. і 200 грн. - це два способи представити одну і ту ж суму грошей в різні моменти часу: 200 грн. через 2 роки рівносильні 181,40 грн. зараз. Процес дисконтування наглядно можна продемонструвати за допомогою графіка (рис. 5.3).
Рис. 5.3. Графічна інтерпретація процесу дисконтування В аналізі інвестицій величини (1+г)" і (1+г)'п часто називають відповідно множниками нарощення і дисконтування.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |




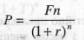 (5.2)
(5.2)