Корреляционная связь, ее признаки, виды. Коэффициент корреляции, определение, свойства, методы вычисления. Метод корреляции рядов Пирсона. Метод корреляции рангов Спирмена.

Многие явления в медицине, так же как в природе и обществе, взаимо­связаны между собой. При проведении статистического исследования часто возникает необходимость проанализировать выявленные связи между различ­ными явлениями и дать обобщающую характеристику. Различают 2 формы проявления связей между явлениями: функциональную и корреляционную.

Функциональная связь означает строгую зависимость одного признака от другого, когда определенному значению одной величины соответствует строго определенное значение другой. Например, радиусу круга соответствует определенная площадь круга; скорость свободно падающего тела определяется величиной ускорения, силой тяжести и временем падения. Функциональная связь характерна для физико-химических процессов.

Корреляционная связь — это такая связь, когда одной и той же величи­не одного признака соответствует несколько значений другого взаимосвязанно­го с ним признака. Врачи и биологи хорошо знакомы с этим видом связи: при одинаковой температуре у различных людей наблюдаются индивидуальные ко­лебания частоты пульса; при одинаковом росте отмечаются различные колеба­ния масс тела.

По форме корреляционная связь:

Прямолинейная связь — равномерные изменения одного признака со­ответствуют равномерным изменениям второго признака при незначительных отклонениях.

Криволинейная связь — равномерные изменения одного признака, со­ответствуют неравномерным изменениям второго признака, причем неравно­мерность имеет определенную закономерность. Общая тенденция в определен­ном моменте изменяет свос направление, дает изгиб.

Направление связи:

Прямая связь (положительная) — если с увеличением одного признака второй также уве­личивается или с уменьшением одного признака другой тоже уменьшается. Обратная связь (отрицательная) — когда с увеличением одного признака, другой, корре­ляционно связанный с ним признак, уменьшается.

Под силой связи следует понимать степень корреляции (степень сопря­женности между признаками).

Измерение силы связи и определение ее направления осуществляется пу­тем вычисления коэффициента корреляции. Существуют следующие методы вычисления коэффициента корреляции: рядов, рангов, путем составления корреляционной решетки.

Степень связи	Величина коэффициента корреляции
При прямой связи (+)	При обратной связи (-)
Связь отсутствует
Связь малая (слабая)	от 0 до + 0,29	от 0 до -0,29
Связь средняя (умеренная)	от 0,3 до + 0,69	от -0,3 до -0,69
Связь большая (сильная)	от 0,7 до+0,99	от -0,7 до -0,99
Связь полная	+1	-1

 

Коэффициент корреляции рядов (r_xy) (Пирсона):

r_xy = , где d = V- M.

Для оценки достоверности коэффициента корреляции вычисляется средняя ошибка коэффициента корреляции:

m_r = – при числе наблюдений более 100;

m_r = – при числе наблюдений от 30 до 100;

m_r = – при числе наблюдений менее 30.

Для оценки величины полученной ошибки следует использовать крите­рий достоверности (t).

t =

Значение критерия (t) оценивается по специальной таблице Стьюдента. Если полученное значение t больше табличного для выбранного уровня дове­рия и числа степеней свободы, то коэффициент корреляции считается досто­верным.

Ко­эффициент корреляции рангов ( ) (Спирмена):

Коэффициент корреляции рангов относится к непарамегрическим критериям. Он используется при необходимости получения быстрого результата, при малом числе наблюдений, а также в тех случаях, когда изучаемые признаки не имеют точных количественных значений или носят описательный характер. Этот метод основан на определении ранга (места) каждого из значений ряда.

= 1 – , где d — раз­ность между ранговыми номерами; n — число парных членов в коррелируемых рядах

Вычисления проводятся по следующему алгоритму:

1) Определить ранги по значению каждой величины ряда. (1,2,3,4…) Если первый ряд (x) ранжируется от меньшего значения к большему, то второй ряд (у) сле­дует ранжировать в том же порядке.

2) Определить разность рангов каждой пары ряда (х) и ряда (у): (d_xy)= (x) - (у). Они в сумме с учетом знаков равны нулю.

3) Возвести в квадрат полученные разности и суммировать их.

4) Рассчитать коэффициент корреляции рангов по формуле.

Прежде чем судить о степени связи между изучаемыми признаками, не­обходимо оценить достоверность коэффициента корреляции рангов.

t =

Полученное значение критерия t оценивается по таблице t-критерия Стьюдента для числа степеней свободы n' = n-2. Коэффициент корреляции незначим, если рассчитанное значение меньше табличного.

 

 

Понятие о непараметрических методах исследования. Критерий соответствия (χ-квадрат), этапы расчета, значение. Понятие о нулевой гипотезе.

Одной из важнейших задач применения математико-статистических методов является оценка достоверности полученных результатов при исследовании и определении наличия связи между какими-либо изучаемыми факторами. Этой задаче отвечает критерий хи-квадрат – коэффициент соответствия или коэффициента согласия.

Как известно, оценка достоверности различий может производиться путем вычисления критерия t (критерия Стьюдента). Однако, он рассматривает различия только между двумя статистическими совокупностями. При сравнении трех и более статистических групп оценка достоверности при помощи критерия t затруднительна, так как попарное сравнение не дает общей оценки. Кроме того, сравниваемые группы имеют не два результата (да, нет), а несколько.

Для этого используют коэффициент соответствия χ² (разработан Пирсоном), который позволяет с одной стороны охарактеризовать наличие связи между явлениями, а с другой - оценить значимость различий между ними.

Критерий соответствия используется для:

– оценки различия в двух или более сравниваемых статистических группахи при нескольких результатах с определенной степенью достоверности. Например, 4 группы больных у которых применимы различные методы лечения; несколько учреждений (отделений) с разными показателями деятельности, легальности; разные группы больных, имеющие разный процент осложнений;

– определения наличия связи между двумя факторами (результат и зависимый признак). Например, зависимость результатов лечения от степени тяжести заболевания, возраста, медико-гигиенических характеристик. Связь между жилищными условиями, материальным обеспечением семьи и т.д. и частотой заболеваний, госпитализаций.

– рассмотрения идентичности распределений частот в двух и более вариационных рядах. Например, одинаково ли распределение больных по содержанию гемоглобина, количеству эритроцитов, белков крови в двух статистических совокупностях (две группы больных с разными заболеваниями, различной степенью тяжести и т.д.)

Применение метода «хи-квадрат» основано на использовании абсолютных значений, представляющих собою распределение признака в совокупности, но не на средних величинах.

Критерий соответствия χ² вычисляется из абсолютных величин и указывает на существенную или несущественную разницу между «фактическими» числами, полученными в процессе исследования, и теоретическими, «ожидаемыми», полученными на основе предположения об отсутствии связи между исследуемыми явлениями, т.е. на основе принятия нулевой гипотезы. Хи-квадрат подтверждает наличие связи, но не устанавливает степень связи. Чем больше величина хи-квадрат, тем больше полученный результат отличается от теоретического.

Сущность метода «хи-квадрат» заключается в определении достоверности отклонений наблюдаемых фактических и теоретических («ожидаемых») данных, получениых при условии отсутствия различия в сравниваемых группах

Таким образом, если Р - фактические данные, P₁ — «ожидаемые» данные, полученные при принятии «нулевой гапотезы», то критерий может быть вычислен но формуле:

χ² = ∑

Оценка полученного значения хи-квадрата производится по специальной таблице. Если значение хи-квадрат больше или равно табличному, то нулевая гипотеза отвергается, чем доказывается связь или влияние изучаемого фактора.

Методика вычисления: (на примере)

1) Приводим фактические данные, из которых следует, чем позднее сделана операция, тем выше будет послеоперационная летальность.

2) Принимаем «нулевую гипотезу». Теоретически предполагаем, что сроки операции от момента госпитализации больных не влияют на частоту летальных исходов и показатель летальности одинаков во все сроки от момента госпитализации больных

3) Вычисляем «ожидаемые» (P₁) данные в соответствия с «нулевой» гипотезой, т.е. «ожидаемые числа» умерших и выздоровевших среди оперированных.

4) Сравнение:

Табличный «хи-квадрат» определяем по числу «степеней свободы», которое равно произведению числа граф, без итоговой, минус единица на число строк без итоговой, минус единица:

n´ = (S - 1) × (R - 1)

Полученное значение χ² намного больше чисел стоящих в строке n´, следовательно нулевая гипотеза отвергается, что позволяет сделать вывод о влиянии на уровни послеоперационной летальности при остром аппендиците сроков операции от момента госпитализации больных.

Можно упростить вычисление показателя χ² (альтернативная вариация), использовав формулу, пригодную для «четырехпольной таблицы». Клетки таблицы условно обозначаются буквами.

χ² =

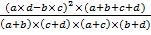
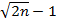Если при вычислении величина n´>30, то по таблице не представляется возможным установить значимость величины χ². В подобных случаях следует определять число k = - и оценивать его следующим образом: k = 1,64, то p=0,05 или 5%, при k = 2,33 — р = 0,01, т.е. 1% и при k > 2,33 — р<0,01, т.е. меньше 1%.