
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика разнообразия изучаемого признака в выборочной совокупности. Среднее квадратичное отклонение, методика вычисления, использование в деят-ти врача.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для характеристики вариационного ряда, помимо средней величины, необходима другая характеристика, позволяющая оценить степень его разнородности. Простыми показателями, характеризующими разнообразие признака в изучаемой совокупности, являются лимит и амплитуда. Лимит — это минимальное и максимальное значения количественного признака. Амплитуда — это разность между наибольшим и наименьшим значением вариант (Vmax - Vmin). Чем меньше амплитуда колебания ряда (степень рассеяния ряда), тем более точно его будет характеризовать средняя арифметическая. Однако лимит и амплитуда не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного признака в пределах вариац ряда является среднее квадратическое отклонение (сигмальное отклонение, σ). Методика расчета среднего квадратического отклонения: 1) Находят среднюю арифметическую величину (М). 2) Определяют отклонения каждой варианты от средней арифметической d = V - М. Сумма всех отклонений равняется нулю. 3) Возводят каждое отклонение в квадрат d2. 4) Перемножают квадраты отклонений на соответствующие частоты: d2×p. 5) Находят сумму произведений ∑ (d2×p). 6) Вычисляют среднее квадратическое отклонение по формуле: σ= Значение среднего квадратического отклонения: 1) Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины, т. е. характеризует колеблемость вариационного ряда. Чем больше среднее квадратич отклонение, тем степень разнообразия данного ряда выше. 2) Среднее квадратич отклон-е используется для сравнительной оценки степени соответствия средней арифметич величины тому вариац ряду, для кот она вычислена. Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм. Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями. Установлено, что при нормальном распределении признака: · 68,3% значений вариант находится в пределах М ± 1σ; · 95,5% значений вариант находится в пределах М ± 2σ; · 99,7% значений вариант находится в пределах М ± Зσ. Такое распределение вариант позволяет считать, что данный вариационный ряд является однородным, а средняя арифметическая величина — типичной. 3) Среднее квадратическое отклонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М ± 1σ обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1σ указывает на отклонение изучаемого параметра от нормы. 4) В медицине правило грех сигм применяется в педиатрической практике для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды, обуви, школьной мебели. 5) Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины. Для сравнения колеблемости двух средних величин, выраженных в различных единицах измерения, используется относительная величина — коэффициент вариации (CV). CV = Чем больше коэффициент вариации, тем большая изменчивость данного ряда. Чем он меньше, тем меньше колеблемость, тем однороднее вариационный ряд, тем типичнее средняя арифметическая величина. Если коэффициент вариации менее 10%, признак характеризуется слабым разнообразием (признак более устойчивый); если коэффициент вариации от 10 до 20% — средним разнообразием; более 20% — сильным разнообразием. Величина коэффициента вариации более 30% свидетельствует о качественной неоднородности совокупности. Ошибка репрезентативности, методика вычисления ошибки средней и относительной величины. Показатели и средние величины, полученные при статистической обработке результатов выборочного исследования, отличаются от данных, которые могли бы быть получены при изучении генеральной совокупности. Обусловлено это тем, что при выборе единиц наблюдения любым из способов, возможны ошибки смещения, то есть такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными, неизбежными, вытекающими из самой сущности выборочного исследования. Поэтому при проведении выборочного исследования необходимо оценивать достоверность его результатов. Для определения степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности (m). Ошибки репрезентативности являются фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования, и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности. Оценка достоверности результатов исследования предусматривает определение: 1) ошибки репрезентативности — т; 2) доверительных границ средних (или относительных) величин в генеральной совокупности; 3) достоверности разности средних (или относительных) величин (по критерию /). Расчет ошибки репрезентативности (mМ) средней арифметической величины (М): mМ = ± mМ = ± Расчет ошибки репрезентативности (тР) относительной величины (Р): mР = ± mР = ±
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.126.33 (0.013 с.) |

 , при n>30 σ=
, при n>30 σ= 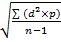 , при n≤30
, при n≤30
 , где σ — среднее квадратическое отклонение; п — численность выборки.
, где σ — среднее квадратическое отклонение; п — численность выборки.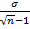 , при малой выборке, n≤30
, при малой выборке, n≤30 , где Р — соответствующая относительная величина (рассчитанная, например, в процентах, промилле…); q — величина, обратная Р, и выражена как (100 - Р%); n — численность выборки.
, где Р — соответствующая относительная величина (рассчитанная, например, в процентах, промилле…); q — величина, обратная Р, и выражена как (100 - Р%); n — численность выборки. , при малой выборке, n≤30
, при малой выборке, n≤30


