Задачи психодиагностики. Организация психодиагностического обследования, требования к инструментарию, этические нормы. БРЮЗГИНА

5. Корреляционные исследования в психологии цели, задачи, специфика по сравнению с истинным экспериментом. Коэффициент корреляции. Особенности контроля. Пример корреляционного исследования. БОНДАРЕНКО

Теория корреляционного исследования разработана английским математиком К. Пирсоном. Стратегия проведения такого исследования заключается в том, что управляемое воздействие на объект отсутствует. План корреляционного исследования несложен. Исследователь выдвигает гипотезу о наличии статистической связи между несколькими психическими свойствами индивида. При этом предположение о причинной зависимости не обсуждается.

Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя или более) переменными. В психологии в качестве переменных могут выступать психические свойства, процессы, состояния и т. п.

Корреляционные связи. «Корреляция» в прямом переводе означает соотношение. Если изменение одной переменной сопровождается изменением другой, то говорят о корреляции этих переменных. Наличие корреляции двух переменных не является свидетельством наличия причинно-следственных зависимостей между ними, но дает возможность выдвинуть такую гипотезу. Отсутствие корреляции позволяет опровергнуть гипотезу о причинно-следственной связи переменных.

Различают несколько типов корреляционных связей:

• прямая корреляционная связь (уровень одной переменной непосредственно соответствует уровню другой переменной);

• корреляция, обусловленная третьей переменной (уровень одной переменной соответствует уровню другой переменной в силу того, что обе эти переменные обусловлены третьей, общей переменной);

• случайная корреляция (не обусловлена никакой переменной);

• корреляция, обусловленная неоднородностью выборки (если выборка состоит двух неоднородных групп, то может быть получена корреляционная связь, не существующая в генеральной совокупности).

Корреляционные связи бывают следующих видов:

– положительная корреляция (повышение уровня одной переменной сопровождается повышением уровня другой переменной);

– отрицательная корреляция (рост уровня одной переменной сопровождается снижением уровня другой);

– нулевая корреляция (свидетельствует об отсутствии связи переменных);

– нелинейная связь (в определенных пределах повышение уровня одной переменной сопровождается повышением уровня другой, а при других параметрах – наоборот. Большинство психологических переменных имеют именно нелинейную связь).

Планирование корреляционного исследования. План корреляционного исследования является разновидностью квазиэкспериментального плана при отсутствии воздействия независимой переменной на зависимые. Корреляционное исследование разбивается на серию независимых измерений в группе испытуемых. В случае простого корреляционного исследования группа однородна. В случае сравнительного корреляционного исследования мы имеем несколько подгрупп, различающихся по одному или нескольким критериям. Результаты таких измерений дают матрицу вида Р х О. Обрабатываются данные корреляционного исследования путем вычисления корреляций по строкам или по столбцам матрицы. Корреляция по строкам дает сравнение испытуемых. Корреляция столбцов дает информацию о связи измеряемых переменных. Часто выявляются временные корреляции, т. е. изменение структуры корреляций во времени.

Ниже рассмотрены основные типы корреляционного исследования.

Сравнение двух групп. Применяется для установления сходства или различия двух естественных или рандомизированных групп по выраженности того или иного параметра. Средние результаты у двух групп сравнивают с помощью t-критерия Стьюдента. При необходимости для сравнения дисперсий показателя в двух группах также может быть использован t-критерий Фишера (см. 7.3).

Одномерное исследование одной группы в разных условиях. План этого исследования близок к экспериментальному. Но в случае корреляционного исследования мы не управляем независимой переменной, а лишь констатируем изменение поведения индивида в разных условиях.

Корреляционное исследование попарно эквивалентных групп. Этот план используется при исследовании близнецов методом внутрипарных корреляций. Близнецовый метод основывается на следующих положениях: генотипы монозиготных близнецов сходны на 100 %, а дизиготных близнецов – на 50 %, среда развития как дизиготных, так и монозиготных пар одинакова. Дизиготные и монозиготные близнецы разбиваются на группы: в каждой – один близнец из пары. У близнецов обеих групп измеряется интересующий исследователя параметр. Затем вычисляются корреляции между параметрами (О-корреляция) и между близнецами (Р-корреляция). Сравнивая внутрипарные корреляции монозиготных и дизиготных близнецов, можно выявить доли влияния среды и генотипа на развитие того или иного признака. Если корреляция монозиготных близнецов надежно выше корреляции дизиготных близнецов, то можно говорить о существующей генетической детерминации признака, в противном случае говорят о средовой детерминации.

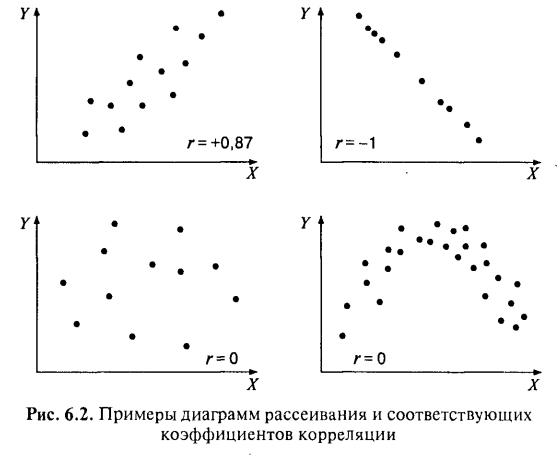
Многомерное корреляционное исследование. Проводится для проверки гипотезы о связи нескольких переменных. Отбирается экспериментальная группа, которая тестируется по определенной программе, состоящей из нескольких тестов. Данные исследования заносятся в таблицу «сырых» данных. Затем эта таблица обрабатывается, подсчитываются коэффициенты линейных корреляций. Корреляции оцениваются на статистические различия.

Структурное корреляционное исследование. Исследователь выявляет различие в уровне корреляционных зависимостей между одними и теми же показателями, измеренными у представителей разных групп.

Лонгитюдное корреляционное исследование. Оно строится по плану временных серий с тестированием группы через заданные промежутки времени. В отличие от простого лонгитюда исследователя интересуют изменения не столько самих переменных, сколько связей между ними.

Задачей любого корреляционного исследования, как и экспериментального, является обобщение, т.е. распространение содержательных выводов об изучаемой зависимости в более широком контексте понимания, чем ограниченный рамками заданных ситуаций, популяций, переменных и т.д. Однако при корреляционном подходе всегда сохраняется многозначность выводов с точки зрения направлений возможных обобщений. Ограничения контроля при получении эмпирических данных определяют и ограничения допустимых выводов.

«Истинные» экспериментальные планы отличаются от других типов исследования прежде всего тем, что, во-первых, в них используются стратегии создания эквивалентных групп (чаще всего стратегии случайного отбора), и во-вторых, в них присутствует экспериментальная и как минимум одна контрольная группа.

Коэффициент корреляции (КК).

При проведении корреляционных исследований существует эмпирическое правило, вытекающее из статистических соображений: рекомендуется, чтобы численность сравниваемых групп была не менее 30–35 человек, поскольку при таком количестве испытуемых значимы на уровне p £ 0,05 часто встречающиеся коэффициенты корреляции порядка 0,35 и выше.

Коэффициент корреляции – двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.

В психологии функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания – график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рисунок ниже). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.

Коэффициент корреляции – количественная мера силы и направления вероятностной взаимосвязи двух переменных, принимает значения в диапазоне от -1 до +1.

Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателей силы связи является абсолютная (без учета знака) величина КК.

Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если соответствует – убывание – обратной (отрицательной). Показателем направления связи является знак КК.

Наследов А. Д. Математические методы психологического исследования. Анализ и интерпретация данных. СПб., 2004

Корреляция метрических переменных

Для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке, применяется коэффициент корреляции r-Пирсона. Сам коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Коэффициент линейной корреляции является параметрическим методом и его корректное применение возможно только в том случае, если результаты измерений представлены в шкале интервалов, а само распределение значений в анализируемых переменных отличается от нормального в незначительной степени. Существует множество ситуаций, в которых его применение целесообразно. Например: установление связи между интеллектом школьника и его успеваемостью; между настроением и успешностью выхода из проблемной ситуации; между уровнем дохода и темпераментом и т. п.

Корреляция ранговых переменных

Если к количественным данным неприемлем коэффициент корреляции r-Пирсона, то для проверки гипотезы о связи двух переменных после предварительного ранжирования могут быть применены корреляции r-Спирмена или τ-Кендалла.

Коэффициент ранговой корреляции Спирмена является непараметрическим аналогом классического коэффициента корреляции Пирсона, но при его расчете учитываются не связанные с распределением показатели сравниваемых переменных (среднее арифметическое и дисперсия), а ранги. Например, необходимо определить связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном».

Коэффициент ранговой корреляции τ-Кендалла является самостоятельным оригинальным методом, опирающимся на вычисление соотношения пар значений двух выборок, имеющих одинаковые или отличающиеся тенденции (возрастание или убывание значений). Этот коэффициент называют еще коэффициентом конкордации. Таким образом, основной идеей данного метода является то, что о направлении связи можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по X совпадает по направлению с изменением по Y, это свидетельствует о положительной связи, если не совпадает – об отрицательной связи, например, при исследовании личностных качеств, имеющих определяющее значение для семейного благополучия. В этом методе одна переменная представляется в виде монотонной последовательности (например, данные мужа) в порядке возрастания величин; другой переменной (например, данные жены) присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов.

Корреляция дихотомических переменных

При сравнении двух переменных, измеренных в дихотомической шкале, мерой корреляционной связи служит так называемый коэффициент j, который представляет собой коэффициент корреляции для дихотомических данных.

Величина коэффициента φ лежит в интервале между +1 и –1. Он может быть как положительным, так и отрицательным, характеризуя направление связи двух дихотомически измеренных признаков. Однако интерпретация φ может выдвигать специфические проблемы. Дихотомические данные, входящие в схему вычисления коэффициента φ, не похожи на двумерную нормальную поверхность, следовательно, неправильно считать, что интерпретируемые значения r_xy=0,60 и φ = 0,60 одинаковы. Коэффициент φ можно вычислить методом кодирования, а также используя так называемую четырехпольную таблицу или таблицу сопряженности.

Шишлянникова Л.М. Применение корреляционного анализа в психологии // Психологическая наука и образование. 2009. Том 14. № 1. С. 98–107.

Подробнее о корреляциях + формулы: Наследов с 67 стр.

http://pzs.dstu.dp.ua/DataMining/multidim/bibl/2004_Matematicheskie_metody_psikhologicheskogo_i.pdf

Особенности контроля.

Общая проблема контроля в корреляционных исследованиях та же, что и в активных экспериментах, - систематическое смешение с побочной переменной. Но в корреляционном исследовании мы не можем активно организовать контрольные условия, а вместо этого должны воспользоваться статистическим контролем смешения. Уравнивание групп в корреляционных исследованиях производится двумя способами.

Подбор пар испытуемых. В случае если число испытуемых невелико, применяется индивидуальный подбор пар. В исследовании психологической приспособленности - подбор пар хорошо и плохо приспособленных испытуемых, которые были бы сходны по интеллекту родителей и социально-экономическому положению. Допустим, что удалось бы найти 50 таких пар. В этом случае между группами уже не было бы различий по названным двум побочным переменным.

Этот метод связан с двумя трудностями. Во-первых, если побочная переменная и в самом деле существенна, то при подборе групп должна обнаружиться диспропорция в количестве хорошо и плохо приспособленных. Большинство хорошо приспособленных испытуемых могут происходить из семей с высоким социально-экономическим положением. Это создаст трудности для нахождения большого числа уравненных пар: среди испытуемых с высоким социально-экономическим положением будет слишком мало тех, у кого плохая психологическая приспособленность. Эта трудность станет особенно серьезной, если мы попытаемся уравнять индивидов не по одной, а по нескольким побочным переменным. При этом число соответствующих пар очень резко сократится. Теоретически никогда нельзя быть уверенным, что проконтролированы все значимые побочные переменные. Практически мы крайне ограничены в числе переменных, которые действительно можем проконтролировать.

Во-вторых, вторая трудность тесно связана с первой - это непредставительность выделенных для исследования испытуемых. Предположим, что для высоко приспособленного индивида характерно иметь родителей интеллигентных, с высоким социально-экономическим положением, а также с хорошей собственной психологической приспособленностью. Однако большая часть таких испытуемых будет отвергнута в процессе составления пар. В то же время это будут те самые испытуемые, чьи родители применяли хорошие способы воспитания. Таким образом, процедура уравнивания может нивелировать влияние процессов воспитания.

Делаем вывод, метод подбора пар несет в себе две опасности: мы можем осуществить недостаточный контроль и мы можем переусердствовать с контролем. Недостаточный контроль приведет к тому, что будет упущена значимая побочная переменная, а избыточный контроль - к тому, что диапазон изменений действительной независимой переменной будет ограничен.

Благодаря методу составления однородных подгрупп в корреляционных исследованиях оказывается возможным многосторонний контроль. Тем не менее, мы никогда не можем знать, действительно ли данный фактор-предпосылка влияет на выбранный поведенческий показатель. Как и в случае подбора пар испытуемых, у нас нет способа узнать, учтены ли все значимые побочные переменные. Более того, когда мы наконец свели наблюдаемый эффект к той переменной, которая кажется решающей, у нее еще остается возможность, что реальным детерминантом поведения была какая-то другая коррелирующая с ней переменная. Эта трудность и породила известное высказывание, что корреляцию не следует путать с причинностью.

Готтсданкер Р. Основы психологического эксперимента: Учеб. пособие.

Пример.

Приведем в качестве примера корреляционные исследования одного из таких вопросов. Маклеод, Эткин и Чафи (McLeod, Atkin & Chaffe, 1972) изучали характер воздействия насилия на телеэкране на уровень агрессии у детей. Они измерили ряд показателей агрессии у выборки 6-10-классников, а также оцепили (использовав самоотчеты) время, в течение которого обычно каждый ребенок смотрел по телевизору сцены насилия. Их интересовал вопрос, есть ли связь между просмотром телепрограмм с эпизодами насилия и уровнем агрессии — то есть были ли наиболее агрессивными те дети, которые наблюдали на телеэкране больше всего насилия? В их исследовании такая связь была обнаружена, что согласуется с гипотезой о провоцировании агрессии телепрограммами с эпизодами насилия.

Исследование Маклеода и др. — пример корреляционного исследования. Оно называется корреляционным, поскольку независимая переменная не подвергалась манипуляциям. Маклеод и др. не осуществляли экспериментальный контроль типа телепрограмм, которые смотрела их выборка, не контролировали они и уровень агрессии, которую демонстрировали дети. И параметры просмотров телепрограмм, и уровень агрессии измерялись в своем естественном виде; при этом цель исследования состояла в выявлении возможного совместного изменения одного показателя с другим. Эта связь может быть положительной, когда повышению одного показателя сопутствует повышение другого. Это как раз результат исследования Маклеода и др. Или же связь отрицательна, когда повышению одного показателя сопутствует понижение другого.

Психология развития [Методы исследования] Миллер Скотт