
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, где число неизвестных превышает число уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При решении ряда текстовых задач их условия требуют введения определенного количества неизвестных. Попытка составить столько же уравнений, сколько и неизвестных, не приводит к успеху. Это происходит по нескольким причинам. Иногда искомая величина представляет собой комбинацию введенных неизвестных (такие ситуации встречаются в задачах на движение). В этих случаях вводятся новые неизвестные и задача решается однозначно. В других задачах необходимо провести анализ полученных уравнений и тогда, если нужно, сделав соответствующие ограничения на неизвестные, также удается получить решение. Возможны, однако, и ситуации, при которых из меньшего количества уравнений удается найти большее количество неизвестных. Заметим, что задачи такого рода встречались и в рассмотренных ранее типах. Задача 18.Три пункта А, В и С соединены прямолинейными дорогами. К отрезку дороги АВ примыкает квадратное поле со стороной, равной 0,5АВ; к дороге ВС примыкает квадратное поле со стороной, равной ВС; кдороге АСпримыкает прямоугольный участок леса длиной, равной АС,и шириной 4 км. Площадь леса на 20 км2 больше суммы площадей квадратных полей. Найти площади квадратных полей и площадь леса. [2, с.154]
Решение: Пусть АВ = 2х, ВС = у, АС = z. Тогда из условия имеем равенство: х2 +у2 +20 = 42 <=> <=> На первый взгляд может показаться, что все условия исчерпаны и пример неразрешим. Но ведь прямолинейные дороги являются сторонами треугольника либо лежат на одной прямой. Тогда z ≤ 2х+у <=> Это возможно только тогда, когда одновременно выполняются равенства Ответ: площадь леса 40 км2, полей — 16 км2 и 4 км2. Задача 19. Первый покупатель купил 14 м ткани первого вида, 5 м второго вида и 9 м третьего вида, за что вместе заплатил 160 евро. Второй приобрел соответственно 4, 13 и 9 метров таких тканей и заплатил за все 128 евро. Третий купил по 5 м ткани каждого вида. Сколько заплатил третий? Какая ткань дороже: первого или второго вида? Решение:Обозначим стоимость тканей первого, второго и третьего вида через х у и zсоответственно. Тогда из условия задачи составляем два уравнения с тремя неизвестными: 14х+5у+9z = 160, 4х + 13у+ 9z=128. Сначала узнаем, сколько уплатил третий покупатель. По условию требуется найти величину 5х + 5у + 5z. Обычно в таких примерах требуемая величина находится из линейной комбинации составленных уравнений: необходимо умножить первое уравнение на некоторое число ά, второе — на β, а затем сложить или вычесть уравнения. Числа ά и β подбираются так, чтобы в результате сложения или вычитания получилась искомая величина. В данном случае к требуемому приводит простое сложение уравнений. Имеем: 18(х + y + z) = 288, т.e. x + y + z =16.Следовательно, третий покупатель уплатил 5 (х + у + z) = 5·16 = 80 евро. В примере нужно получить и второй ответ: что большее х или у?В таких случаях сначала из одного из уравнений исключается третье неизвестное. Вычтем из первого уравнения системы второе. Получим 10х - 8у= 32 <=> 5х — 4у = 16. Из этого уравнения неясно, что больше: х или у. Однако из полученного соотношения х + у + z = 16 следует, что х < 16, у <16, z <16. Тогда 5х -4у = 4(х - у)++ у = 16. Так как у < 16, то, очевидно, выполняется 4(х – у) > 0, т. е. х > у. Ответ: третий покупатель уплатил 80 евро; первая ткань дороже второй. Задача 20. Имеется два различных сплава меди со свинцом. Если взять 1 кг первого сплава и 1 кг второго сплава и переплавить их, то получится сплав, содержащий 65 % меди. Известно, что если взять два некоторых куска — кусок Аи кусок В первого и второго сплавов соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится сплав с содержанием 60 % меди. Какова масса меди, содержащейся в сплаве, получающемся при совместной переплавке куска первого сплава, равного по массе куску В, и куска второго сплава, равного по массе куску А. [2, с.155] Решение:Пусть концентрация меди в первом и втором сплавах равна соответственно х и у. Тогда, если сплавить по одному килограмму обоих сплавов, то получим сплав, в котором концентрация меди равна х + у = 1,3, А + В = 7, хА + уВ = 4,2 Однако и найти требуется не все неизвестные, а величину (хВ + уА).Перемножим левые и правые части первого и второго уравнений системы. Имеем: (х + у)(А + В) = 9, 1 <=> (хА + у В) + (хВ + у А) = 9,1 Учитывая третье уравнение, получаем хВ + уА = 9,1 - 4,2 = 4,9 кг. Ответ: масса меди 4,9 кг. Задача 21.Резервуар наполняется водой по пяти трубам. Первая труба наполняет резервуар за 40 мин; вторая, третья и четвертая, работая одновременно, — за 10 мин; вторая, третья и пятая — за 20 мин и, наконец, пятая и четвертая — за 30 мин. За какое время наполнят резервуар все пять труб при одновременной работе? [2, c.157] Решение:Пусть первая, вторая и т. д. трубы наполняют (каждая в отдельности) резервуар за х1, х2, х3, х4, х5мин (индекс у неизвестных соответствует номеру трубы). Тогда за одну минуту они заполнят соответственно
Фактически необходимо, найти выражение m =
Ответ:за Задача 22.Имеется два сплава с различным содержанием меди. Масса первого сплава т кг, масса второго сплава п кг. От каждого из сплавов отделили по одинаковому куску равной массы и каждую из этих частей сплавили с остатком другого куска. В новых сплавах процентное содержание меди стало одинаковым. Какова масса каждого из отрезанных кусков? Решение:Пусть с1 и с 2 — концентрации меди соответственно в первом и втором сплавах, а х — массы отдельных кусков сплавов. Тогда масса меди в первом сплаве составляет с1т, во втором — с2п. В отделенном куске х от первого сплава меди содержится cl x, а в куске от второго сплава — с2х. После того как каждый сплав сплавили с куском другого сплава, в первом сплаве меди стало с1 т - с1 х + с2х, а во втором — с2п- с2х + clx. Приравнивая новые концентрации сплавов, получаем уравнение:
Таким образом, получим одно уравнение с тремя неизвестными с1, с2 и х. Избавившись от знаменателей, перенеся все величины влево и перегруппировав их, находим: (с1 - с2 )(тп – х (т + п)) = 0. Так как по условию с1 ≠ с2, то имеем: Ответ: отрезали Задача 23.Стройотряд состоит из 32 бойцов, каждый из которых владеет одной или двумя строительными профессиями: каменщик, бетонщик и плотник. Плотников в 2 раза больше, чем бетонщиков, и в n раз меньше, чем каменщиков (3 ≤ n ≤ 20, n – натуральное число.). Сколько бойцов в отряде владеет только одной профессией, если число бойцов, владеющих двумя профессиями, на 2 больше, чем число бойцов, владеющих профессией плотника? Решение:Пусть х – число бойцов, владеющих одной профессией, у – двумя, u - число плотников среди бойцов отряда, v - число бетонщиков, w - число каменщиков, так как всего бойцов 32, то х + у = 32. по условию u = 2v, w = nu, y= u + 2. таким образом, получаем четыре уравнения и шесть неизвестных. Пятое уравнение получаем из условия равенства специальностей. С одной стороны, их количество равно х + 2у, а с другой – u+ v + w, т. е. х + 2у = u+ v + w. Выразим в уравнениях неизвестные через u: v = u/2, w = nu, y = г +2, х = 30 – u и подставим в последнее уравнение, получим: 34 = u Ответ:в отряде 26 бойцов, владеющих только одной профессией. Задача 24.Два поезда отправляются навстречу друг другу с постоянными скоростями, один их А в В, другой из Вв А. Они могут встретиться на на середине пути, если поезд из А отправиться на 1,5 часа раньше. Если бы оба поезда вышли одновременно, то через 6 часов расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? [2, с.106] Решение:Пусть расстояние между А и В равно s, а скорости поездов, идущих из А в В и из В в А соответственно равны v1 и v2. Если поезд из А отправился на 1,5 часа раньше, то за это время он прошел бы расстояние 1,5v1, и между поездами было бы расстояние (s-1,5v1). Тогда время встречи поездов определяется по формуле: Если бы оба поезда вышли одновременно, то за 6 часов они прошли бы расстояние 6v1 и 6v2. Между ними оставалось бы расстояние, равное десятой части первоначального, т. е. за 6 часов вместе они прошли бы 0,9 всего расстояния. Поэтому 6v1 + 6v2= 0,9s. Итак, имеем систему двух уравнений с тремя неизвестными:
В условии же требуется найти время, за которое каждый поезд проходит весь путь, т. е. х – у = 3ху, 6х +6у = 0,9. Выразив из второго уравнения у и подставив в первое уравнение, получим следующее уравнение: 3х2 - 2,45х - 0,15 = 0. Оно имеет корни: Ответ: поезд, идущий из В в А, затрачивает на весь путь 12 ч, а поезд, идущий из А в В – 15ч.
ЛИТЕРАТУРА 1. 3000 конкурсных задач по математике /Под ред. проф. Н.А.Бобылева. - М.: Рольф, 1997. 2. Азаров А.И., Барвенов С.А., Федосенко B.C. Текстовые задачи. - Мн.: Аверсэв, 2005. 3. Азаров А.И., Барвенов С.А., Федосенко B.C., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи.- Мн.: ТетраСистемс, 1998. 4. Барабанов Е.А., Воронович И.И., Каскевич В.И., Мазаник С.А. Задачи районного тура Минской городской математической олимпиады школьников. – Мн., Фаритекс, 2002. 5. Бахтина Т. П. Готовимся к олимпиадам, турнирам и математическим боям. Математикон 8. - Мн.: Аверсэв, 2003. 6. Габринович В.А., Громак В.И. Решим любую задачу. Задачи на экзаменах по математике в БГУ в 1995 году с решениями и комментариями: учеб пособие. - Мн.: Белгосуниверситет, 1996. 7. Кипнис И.М. Задачи на составление уравнений и неравенств. - М.: Просвещение, 1980. 8. Лурье М.В. Задачи на составление уравнений. Техника решения. - М.: УНЦ ДО, 2004. 9. Лурье М.В., Александров Б.И. Задачи на составление уравнений. - М.: Наука, 1990. 10. Мельников И.И., Сергеев И.Н. Как решать задачи по математике на вступительных экзаменах. - М.: Изд-во Моск. ун-та, 1990. 11. Фарков А.В. Математические олимпиады в школе 5 – 11 классы. - М.: Айрис пресс, 2003.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |


 х2 +
х2 +  у2 +5 = z.
у2 +5 = z. .
. , откуда х = 4, у = 2.Тогда z = 10 и требуемые площади легко находятся. Кроме того, мы установили, что А, В и Снаходятся на одной прямой.
, откуда х = 4, у = 2.Тогда z = 10 и требуемые площади легко находятся. Кроме того, мы установили, что А, В и Снаходятся на одной прямой. . Возьмем кусок А первого сплава. В нем содержится хА меди. В куске В второго сплава содержится уВ меди. Так как общая масса нового сплава равна А + В = 7 и в нем содержится (хА + у В) кг меди, то ее концентрация в сплаве будет
. Возьмем кусок А первого сплава. В нем содержится хА меди. В куске В второго сплава содержится уВ меди. Так как общая масса нового сплава равна А + В = 7 и в нем содержится (хА + у В) кг меди, то ее концентрация в сплаве будет  , т. е. (хА + уВ) = 4,2. В куске Впервого сплава содержится х Вмеди, а в куске А второго сплава меди будет уА. Требуется узнать, чему равна масса меди в новом сплаве, т. е. чему равна величина (хВ+уА). Использовав все условия задачи, удалось составить только три уравнения с четырьмя неизвестными:
, т. е. (хА + уВ) = 4,2. В куске Впервого сплава содержится х Вмеди, а в куске А второго сплава меди будет уА. Требуется узнать, чему равна масса меди в новом сплаве, т. е. чему равна величина (хВ+уА). Использовав все условия задачи, удалось составить только три уравнения с четырьмя неизвестными: часть резервуара. Из условия задачи можно составить следующую систему уравнений:
часть резервуара. Из условия задачи можно составить следующую систему уравнений:
 . Тогда искомое время будет равно
. Тогда искомое время будет равно  . Умножим первое уравнение на второе, а затем сложим все уравнения. Получим
. Умножим первое уравнение на второе, а затем сложим все уравнения. Получим т. е. т =
т. е. т =  . Таким образом, все пять труб заполнят резервуар, работая вместе, за
. Таким образом, все пять труб заполнят резервуар, работая вместе, за  часа.
часа.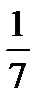 часа.
часа.
 . Легко проверить, что х < т и х < п, поэтому найденное значение является ответом.
. Легко проверить, что х < т и х < п, поэтому найденное значение является ответом. кг.
кг. .нечетное натуральное число 2n+1 должно быть среди делителей числа 68. Оно единственное и 2n + 1=17, n = 8. (n удовлетворяет условию, наложенному на него). Тогда u = 4, х = 26.
.нечетное натуральное число 2n+1 должно быть среди делителей числа 68. Оно единственное и 2n + 1=17, n = 8. (n удовлетворяет условию, наложенному на него). Тогда u = 4, х = 26. . За это время поезд из В в А проходит половину пути, т. е.:
. За это время поезд из В в А проходит половину пути, т. е.:  .
. профессией плотника?адеющих дв профессиями: каменщик, бетонщик и плотн
профессией плотника?адеющих дв профессиями: каменщик, бетонщик и плотн 
 . Разделим обе части первого уравнения на s2 , а второго на s. Обозначим:
. Разделим обе части первого уравнения на s2 , а второго на s. Обозначим:  получим систему двух уравнений с двумя неизвестными:
получим систему двух уравнений с двумя неизвестными: . Поскольку у > 0, то подходит только первая пара.
. Поскольку у > 0, то подходит только первая пара.


