
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство неравенств методом математической индукции.Содержание книги
Поиск на нашем сайте
Доказательство методом математической индукции основано на следующей аксиоме: если предложение, в формулировку которого входит натуральное число п, истинно при п=1 и из его истинности при n=k (где Таким образом, доказательство по методу математической индукции проводится следующим образом: 1) доказываемое утверждение проверяется при п 2) предполагая справедливость утверждения при n=k, доказывается справедливость утверждения для n=k+1. Некоторые утверждения справедливы не для всех натуральных п, а для п, начиная с некоторого числа р. В таком случае первый шаг доказательства – это проверка справедливости утверждения для п=р П р и м е р. Доказать, что если
Доказательство. При n=3 неравенство верно: В самом деле, имеем: Но Согласно методу математической индукции можно сделать вывод о том, что доказываемое неравенство справедливо при всех
Доказательство неравенств методом полной индукции. Полная индукция – это метод рассуждений, при котором вывод делается на основании рассмотрения всех случаев, возможных по условию задачи. П р и м е р. Доказать, что
Доказательство. Рассмотрим случаи:
1)
Неравенство верно. 2) Тогда 3) Тогда Мы рассмотрели все возможные случаи. Значит неравенство верно для
6. Доказательство неравенств с помощью методов математического анализа. В этом случае доказательство неравенств сводят к исследованию соответствующих функций с помощью производных.
П р и м е р. Доказать неравенство Доказательство. Перепишем неравенство в виде: Рассмотрим функцию Найдём производную
Литература 1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000 Тема: Иррациональные уравнения и неравенства. План 1. Иррациональные уравнения, основные методы их решения. 2. Иррациональные неравенства.
Иррациональные уравнения. Иррациональными называются уравнения и неравенства, содержащие переменную под знаком корня или под знаком возведения в дробную степень. Все корни чётной степени, входящие в уравнение, являются арифметическими, т.е. если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то значение корня положительно. Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения. Основные методы решения иррациональных уравнений: 1. возведение обеих частей уравнения в одну и ту же степень; 2. замена переменной; 3. умножение обеих частей уравнения на одну и ту же функцию; 4. применение свойств функций, входящих в уравнение. Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например возведение обеих частей уравнения в чётную степень, приводят к уравнению-следствию. Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения. Возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в чётную степень. Рассмотрим несколько примеров.
Пример 1. Решим уравнение Решение. Возводим обе части уравнения в квадрат, получаем:
Проверка показывает, что только Ответ: -4.
Пример 2. Решим уравнение
Решение. Выполним замену. Обозначим: Тогда Исходное уравнение принимает вид:
Полученное уравнение равносильно системе:
Из получившейся системы, имеем: Возвращаемся к подстановке, получаем:
Ответ: 1; Пример 3. Решим уравнение Решение: Пусть Тогда имеем:
Откуда последовательно получаем:
Возвращаясь к первоначальным подстановкам, получим:
Откуда С помощью проверки убеждаемся, что оба корня являются корнями исходного уравнения.
Ответ: 1; -15. Пример 4. Решим уравнение Решение: Рассмотрим функцию Исходное уравнение принимает вид:
Ответ: 5.
Иррациональные неравенства. Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т.д. Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению: 1) Неравенство вида
2) Неравенство вида 3) Неравенство вида 4) Неравенство вида
Пример 5. Решим неравенство
Решение. Введём новую переменную
Решая это неравенство и возвращаясь к исходным переменным, получаем: Ответ: Пример 6. Решим неравенство
Решение: Перепишем неравенство в виде: Это неравенство равносильно системе неравенств:
Пример 6. Решим неравенство Решение: Рассмотрим функцию Ответ: нет решений. Литература 1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Текстовые задачи План
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 7004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.51 (0.007 с.) |

 ) следует, что оно истинно и при
) следует, что оно истинно и при 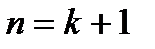 , то оно истинно при всех натуральных значениях п.
, то оно истинно при всех натуральных значениях п. =1;
=1; , то
, то
 . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что
. Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что  , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что
, и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что 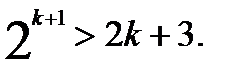
 . Итак,
. Итак, 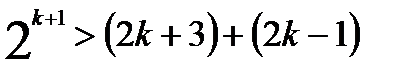 .
. при любом натуральном значении k. Следовательно, тем более
при любом натуральном значении k. Следовательно, тем более  .
.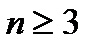 .
. если
если 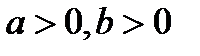 .
. . Получаем
. Получаем , т.к.
, т.к. 
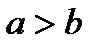 , т.е.
, т.е.  .
. . Неравенство справедливо.
. Неравенство справедливо. т.е.
т.е.  .
. . Неравенство справедливо.
. Неравенство справедливо. .
.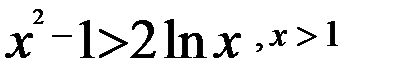
 .
.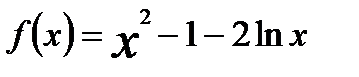 .
.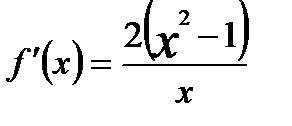 . При
. При  ,
,  . Это значит, что при
. Это значит, что при 
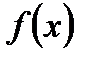 возрастает, причём
возрастает, причём  . Поэтому при
. Поэтому при 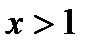
 .
. .
.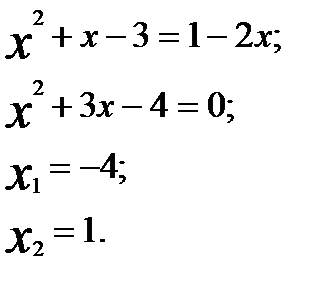
 является корнем исходного уравнения.
является корнем исходного уравнения.
 заметим, что
заметим, что  .
.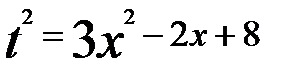 и
и 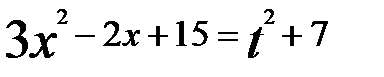 .
.
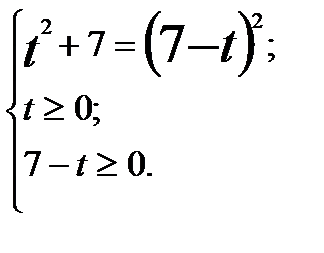
 .
.
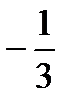 .
. .
.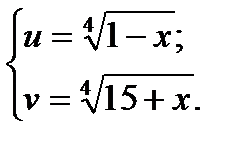




 .
. .
.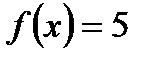 .
. . Функция
. Функция 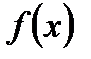 монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что
монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что 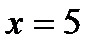 является корнем уравнения.
является корнем уравнения. равносильно системе
равносильно системе
 равносильно неравенству
равносильно неравенству  .
. равносильно совокупности систем
равносильно совокупности систем 
 равносильно системе
равносильно системе
 .
.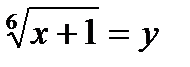 . Тогда исходное неравенство принимает вид:
. Тогда исходное неравенство принимает вид: .
. .
. .
.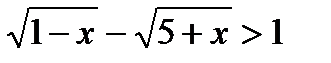 .
. .
. Откуда получаем
Откуда получаем  .
. .
. . Область определения этой функции
. Область определения этой функции  . Функция
. Функция  возрастает на всей области определения, причём
возрастает на всей области определения, причём 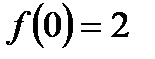 . Значит, неравенство
. Значит, неравенство 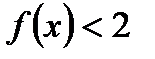 решений не имеет.
решений не имеет.


