
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические уравнения. Основные методы их решения.Содержание книги
Поиск на нашем сайте
При решении логарифмических уравнений во многих случаях приходится использовать свойства логарифмов. Напомним их. Определение. Логарифмом числаb по основанию а
Свойства логарифмов: 1. 2. 3. 4. 5. 6. 7. 8. Заметим, что эти преобразования неравносильны. Применение этих формул в одну сторону приводит к расширению области определения, а в другую – к сужению. Уравнение вида
Уравнение вида
С помощью тождественных преобразований более сложные логарифмические уравнения приводятся к простейшим. При решении также используются более общие методы решения уравнений: разложение на множители, введение новых переменных, функционально-графический.
Рассмотрим несколько примеров.
Пример 10. Решим уравнение
Решение. Выполняем последовательно преобразования:
Необходима проверка:
Ответ:
Пример 11. Решим уравнение
Решение. Переходим к новому основанию и выполняем последовательно преобразования:
Введём новую переменную:
Получаем уравнение:
Откуда Возвращаемся к подстановке, получаем: Откуда
Ответ:
Логарифмические неравенства.
Решение логарифмических неравенств вида
Основано на следующих двух теоремах:
Теорема 1. Если Теорема 2. Если Пример 12. Решим неравенство
Решение. Это неравенство можно переписать так:
В соответствии с теоремой 2 получаем систему неравенств:
Эта система равносильна неравенству
Из которого получаем При решении логарифмических неравенств используется также обобщённый метод интервалов. Пример 13. Решим неравенство
Решение. Выполняем последовательно преобразования неравенства:
Для функции
Отмечаем на координатной прямой, определяем знаки функции на полученных промежутках: Выбираем решение:
Литература: 1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М., 1999 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000 Графики функций и уравнений План 1. Простейшие преобразования графиков функций Построение графиков функций, выражение которых содержит знак модуля Построение графиков суммы, разности, произведения и частного функций
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

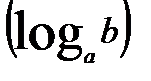 называется показатель степени, в которую надо возвести а, чтобы получить b.
называется показатель степени, в которую надо возвести а, чтобы получить b.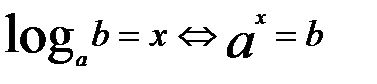 ,
, 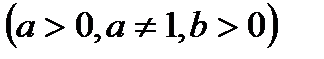
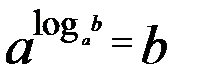
 , где
, где 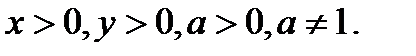
 , где
, где  где
где 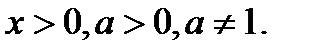
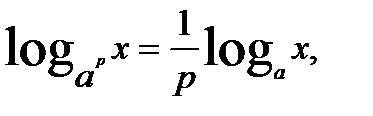 где
где 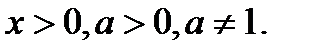
 где
где 
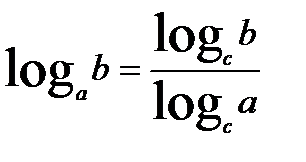 ,где
,где 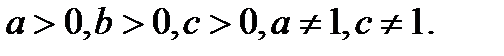
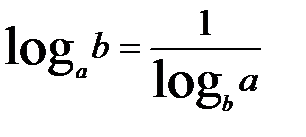 , где
, где 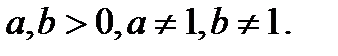
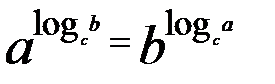 , где
, где 
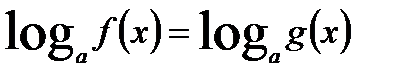 равносильно системе:
равносильно системе:
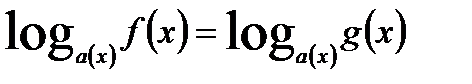 равносильно системе:
равносильно системе:
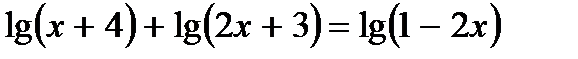

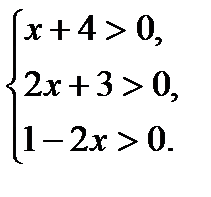
 .
.
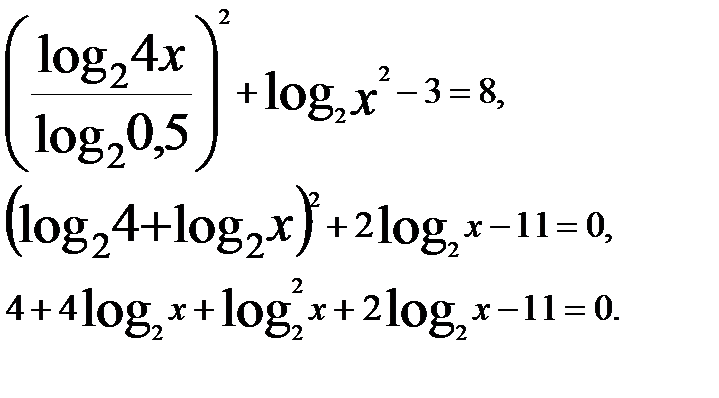

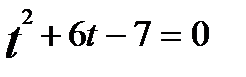 .
.


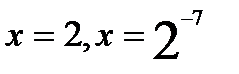 .
. , где
, где 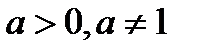
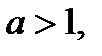 то неравенство
то неравенство  равносильно системе неравенств
равносильно системе неравенств 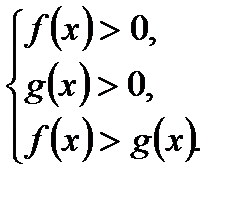
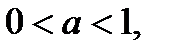 то неравенство
то неравенство 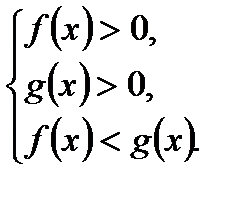
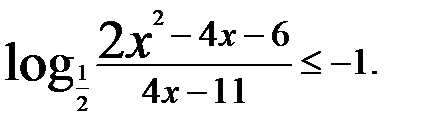
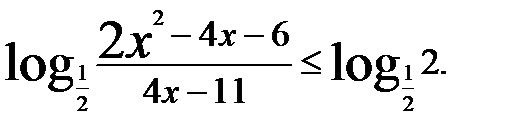
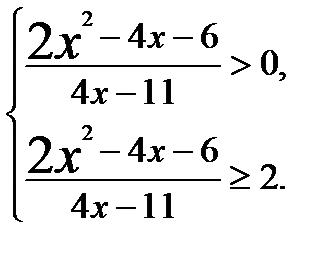

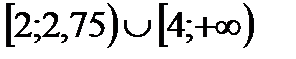 -- решение заданного неравенства.
-- решение заданного неравенства.
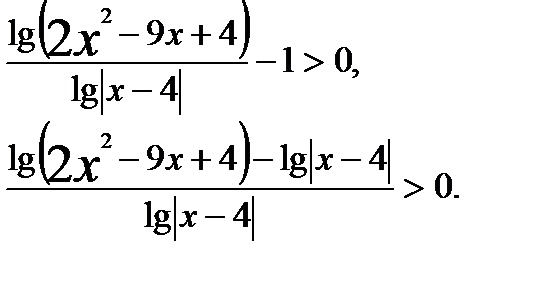
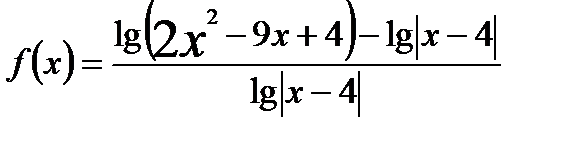 находим область определения и значения аргумента, при которых функция принимает значение,равное нулю:
находим область определения и значения аргумента, при которых функция принимает значение,равное нулю:
 .
.



