
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нестандартные текстовые задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 2.1. Задачи, которые решаются при помощи неравенств Условия большого количества нестандартных задач сформулированы таким образом, что введенные неизвестные связываются между собой не только уравнениями, но для них существуют и определенные ограничения, математическая запись которых представляет собой некоторую систему неравенств. Возможны случаи, когда уравнения вообще составить невозможно, а для определения неизвестных приходится решать систему неравенств. В абсолютном большинстве случаев решением неравенства является множество, представляющее собой некоторый интервал или отрезок на действительной оси. Возникает вопрос: каким образом из этого множества выбрать единственное значение неизвестной величины, являющееся решением задачи? Здесь возможны три ситуации. В первом случае одна и та же неизвестная величина удовлетворяет двум неравенствам. Допустим, что решением первого неравенства является искомая величина а ≤ х ≤ b, а при решении второго неравенства получим, что b ≤ х ≤ c. Очевидно, что единственным значением х будет х = b. Во втором случае из условия задачи ясно, что искомые величины могут принимать только целочисленные значения. Это и является дополнительным условием для определения неизвестных. Наконец, в третьем случае имеется ряд косвенных признаков, определенных условиями задач, по которым возможно получить однозначное решение. Характер некоторых таких признаков станет более ясным из анализа рассмотренных ниже примеров. Задача 1. В триседьмом царстве живут драконы. У каждого дракона одна, две или три головы. Может ли у 40% драконов быть 70% голов? Решение. Пусть х – число драконов, а у – общее число голов у них. Предположим, что какие-то 40% драконов имеют 70% голов. Тогда, поскольку каждый из этих драконов имеет не более трех голов, 0,7у ≤ 3∙0,4х. С другой стороны, поскольку остальные 60% драконов имеет 30% голов и у каждого из них не менее одной головы, 0,3у ≥ 0,6х, но эти неравенства не могут выполняться одновременно, т.к. они равносильны соответственно 7у ≤ 12х и 6у ≥ 12х. Поэтому у 40% драконов не может быть 70% голов. Ответ: не может. Задача 2. Три школьника, у каждого из которых было несколько бумажных рублей, подошли к киоску с мороженым. Петя, имевший меньше всех — всего 1 рубль, купил две порции и ушел. Остальные двое решили купить как можно больше мороженого. Оказалось, что Коля смог бы купить 6 порций, а Вася — 11 порций. Если бы они сложили свои капиталы, то на 18 порций им все равно не хватило бы. Сколько стоит порция мороженого в этом киоске? Решение. Пусть порция мороженого стоит х копеек. Так как Пете хватило рубля на две порции, то х < 50. Если бы у Коли было не меньше четырех рублей, то ему хватило бы денег на 8 порций, а он смог купить только 6. Следовательно, у него было 2 или 3 рубля. Рассмотрим оба случая. Пусть у Коли 2 рубля; он может купить 6 порций мороженого, но не может купить 7 порций. Тогда порция мороженого стоит больше Если х ≥ 46, то 506 ≤ 11х < 550, откуда следовало бы, что у Васи не меньше 6 рублей. Но тогда он смог бы купить не меньше 12 порций мороженого. Следовательно, 43 < х ≤ 45 и 473 < 11х ≤ 495, т. е. у Васи было 5 рублей, а вместе с Колей - 8 рублей, причем на 18 порций этого не хватало. Поэтому х > 800/18 = 44,4..., откуда х = 45 копеек. Ответ: 45 копеек. Задача 3. В волейбольном турнире приняло участие несколько команд. После того, как турнир закончился, выяснилось, что среди любых четырех команд найдутся две, которые в играх между командами этой четверки набрали одинаковое число очков. Какое наибольшее число команд могло участвовать в этом турнире? (За победу команде присуждается одно очко, за поражение – 0, ничьих в волейболе не бывает) Решение: Предположим, что найдется команда А, которая выиграла не менее 4 игр, например, у команд В, С, Д, Е. Рассмотрим любые три команды, пусть это будут В, С, Д, из этих четырех проигравших. Легко увидеть, что при выполнении условия задачи команды В, С, Д, в играх между командами четверки А, В, С, Д должны были набрать ровно по одному очку каждая. Поэтому каждая из этих команд в играх между собой должна выиграть одну игру и одну игру проиграть. Очевидно, что это условие должно выполняться для любой тройки команд из четверки В, С, Д, Е. Но это означает, что в играх между командами этой четверки каждая из них набрала одинаковое количество очков, чего не может быть, ибо в играх между четверкой команд разыгрывается 4∙ Ответ: 7 команд. Задача 4. Населенные пункты А, В и С соединены прямолинейными дорогами. К отрезку пути АВ прилегает квадратная делянка леса, сторона которой равна — АВ, к отрезку пути ВС - квадратная делянка леса, сторона которой ВС, а к отрезку АС — прямоугольное поле, длина которого АС и ширина 5 км. Площадь поля на 31,25 км больше, чем сумма площадей делянок леса. Найдите площадь поля. [5, с.183] Решение:Обозначим АВ = х, ВС = у, AC = z. По условию 5z = то Ответ:62,5 км2. Задача 5. Не дождавшись трамвая на остановке А, пассажир пошел к следующей остановке В. Пройдя Решение: Пусть искомая скорость пассажира равна υ км/ч. До остановки А он потратит времени
Из первого неравенства следует υ ≥ Ответ: пассажир должен бежать со скоростью не менее 8 км/ч. Задача 6.В автогонках принимают участие несколько команд, имеющих одинаковое число автомобилей марки «Волга» и «Жигули», причем в каждой команде их меньше 7. Если в каждой команде число автомобилей марки «Волга» оставить без изменения, а число «Жигулей» увеличить в 3 раза, то общее число будет на 50 больше общего числа «Волг», а число автомобилей в каждой команде превысит 12. Определить число команд, участвующих в гонках, и число «Волг» и «Жигулей» в каждой команде. Решение: Пусть k — число команд, участвующих в гонках, a m и n — число «Волг» и «Жигулей» в каждой команде. В каждой команде число машин n + m < 7. Далее из условий примера составим еще два соотношения: 3nk - mk = 50 и m + 3n > 12. Таким образом, имеем следующую систему уравнений: k(3n - m) = 50, m + n - 7 < 0, l2 - m - 3n < 0.
Рассмотрим и другой подход. Непосредственно из двух последних неравенств находим n > Так как m + n ≤ 6, то (m + n) ≤ 3. Из последнего неравенства системы имеем: 12 - m - n < 2n, т. е. n > 6 – Но m ≥ 1, n ≥ 3, т.е. Итак, n может принимать только значения 4 и 5. Так как m + n ≤ 6, то m может принимать только значения 1 и 2. Из первого уравнения видно, что число 3n - m должно быть делителем 50. Проверка показывает, что только при n = 4 и m = 2 (3n - m = 10) эта величина является делителем числа 50. Из этого уравнения имеем теперь: k = Ответ: участвуют 5 команд, 2 «Волги» и 4 автомобиля «Жигули».
2.2. Задачи с целочисленными неизвестными Задача 7. В футбольном турнире участвовало 10 команд, каждая команда сыграла с каждой из остальных по одному разу. Какое наибольшее число очков в турнире могла набрать команда, набравшая в нем меньше всего очков (за победу команда получает 3 очка; проигрыш – 0; за ничью - обе команды по 1 очку). Решение:Пусть х очков набрала команда, набравшая в турнире меньше всех очков. Тогда любая другая набрала не меньше х + 1 очков. Поэтому общее количество очков, набранных всеми командами, не менее чем х + 9(х + 1) = 10х + 9. С другой стороны, в каждом из 10∙ Ответ:12 очков. Задача 8. Есть 2000 долларов на путевки в дома отдыха. Путевки есть на 15, 27 и 45 дней. Стоимость их 21 доллар, 40 долларов и 60 долларов соответственно. Сколько и каких путевок надо купить, чтобы истратить все деньги и чтобы число дней отдыха было наибольшим?[2, с.176] Решение:Пусть надо купить х путевок первого типа, у путевок второго типа и я путевок третьего типа. По условию задачи 21х + 40у + 60z = 2000. это единственное уравнение, которое можно составить. Кроме того, мы знаем, что х, у, z – натуральные числа и выражение 15х + 27у + 45z (равное общему числу дней отдыха) максимально. Выясним, какой вид путевок самый выгодный. 1 доллар по путевкам первого типа дает 15/21 дней отдыха, по путевкам второго типа 21/40, а по путевкам третьего типа 45/60 дней. Сравнивая эти дроби, выясняем, что путевки третьего типа самые выгодные, т. к. третья дробь больше всех остальных. Получим ограничения на х и у: на 420 долларов можно купить либо 20 путевок первого типа, либо 7 путевок третьего типа. При этом число дней будет 300 и 315 соответственно. Значит, при оптимальном выборе х, у, z будет выполняться неравенство х < 20. действительно, если х ≥ 20, то можно вместо 20 путевок первого типа купить 7 путевок третьего. Тогда потраченная сумма будет такая же, а число дней увеличиться, т. е. выбор таких x, y, z при которых х ≥ 20, не оптимален. Далее, на 120 долларов можно купить 3 путевки второго типа или 2 третьего типа. При этом число дней отдыха будет 81 и 90 дней соответственно. Значит, у < 3. перепишем первое уравнение в виде: 21х=2000-40у-60z=10(200-4y-6z) Отсюда видно, что 21х делиться на 10 и, следовательно, х тоже делиться на 10. значит, х=0 либо х=10, а у – одно из чисел 0, 1, 2. Переберем все возможные случаи. Пусть х=0, тогда 40у + 60z = 2000 2у + 3z = 100. Если у = 0, то z = 100/3, чего не может быть. Если у = 1, то 3z = 100-2 = 98 и опять решений нет. Если у = 2, то z = 32. Пусть х = 10. тогда 40у+ 60z = 2000-210 4у + 6z = 179. Это уравнение целых решений не имеет, т. к. слева стоит четное число, а справа – нечетное. Итак, единственная возможность, которая осталась, это х = 0, у = 2, z = 32. Ответ:нужно купить 2 путевки второго типа и 32 третьего. Задача 9. Квартал застроен пятиэтажными и девятиэтажными домами, причем девятиэтажных домов меньше, чем пятиэтажных. Если число девятиэтажных домов увеличить вдвое, то общее число домов станет более 24, а если увеличить вдвое число пятиэтажных домов, то общее число домов станет менее 27. Сколько пятиэтажных и девятиэтажных домов построено? Решение: Обозначим через m и n число пятиэтажных и девятиэтажных домов соответственно. Реализуя условия задачи, получаем следующую систему неравенств: n < m; 2n + m > 24; 2m + n < 27. Напомним, что при исключении неизвестных из неравенств лучше всего образовать однонаправленные неравенства: n - m < 0; 24 - 2n – m < 0; 2m + n – 27 < 0. Теперь можно одно неравенство умножить на одно положительное число, второе — на другое и их сложить. В таком случае мы получим равносильные неравенства. Будем последовательно исключать неизвестные m и n. Умножив первое неравенство на 2 и сложив со вторым, получим 24 - 3m < 0, т. е. m > 8. Умножив первое неравенство на 2 и сложив с третьим, получим 3n - 27 < 0, т. е. n < 9. Теперь умножим второе неравенство на 2 и сложим с третьим. Находим: 21- 3n < 0, т. е. n > 1. Наконец, умножим третье неравенство на 2 и сложим со вторым: 3m - 30 < 0, т. е. m < 10. Итак, получили ограничения для неизвестных m и n: 8 < m < 10, 7 < n <9. Так как m и n — целые положительные числа, то очевидно, что m= 9, n = 8. Ответ: 9 пятиэтажных и 8 девятиэтажных домов. Задача 10.Мастер делает за 1ч целое число деталей, большее 5, а ученик на 2 детали меньше. Один мастер выполняет заказ за целое число часов, а 2 ученика на 1ч быстрее. Из какого количества деталей состоит заказ? Решение: Пусть мастер делает п деталей в час и выполняет всю работу за t часов. Из условия задачи получаем систему n t=(n-2)(t-1), n > 5, Из уравнения системы получаем п = 4 + Ответ: 24 детали. Задача 11.Линию, связывающую города А и Б, обслуживают самолеты трех типов. Каждый самолет первого, второго и третьего типов может принять на борт соответственно 230, 110 и 40 пассажиров, а также 27, 12 и 5 контейнеров. Все самолеты линии могут принять на борт одновременно 760 пассажиров и 88 контейнеров. Найти число действующих на линии самолетов. Решение: Пусть количество самолётов 1-го, 2-го и 3-го типов равны соответственно, п, т и k. Из условия задачи получаем систему: 230n+110m+40k=760, 27n+12m+5k=88, m+n+k ≤ 8. Вычитаем из второго уравнения первое, уменьшенное в 10 раз, получим уравнение 4n+m+k=12. Т.к. т, п, k целые неотрицательные числа, то все возможные значения величины п суть числа 0, 1, 2, 3. При п=0, m+k =12 и не выполнено неравенство в системе. При п = 1, m+k =8 и неравенство снова не выполнено. При п = 3, m + k =0, то есть m = 0 и k = 0. Но тогда не выполнены уравнения системы. Следовательно, п=2. Тогда m+k=4, причём неравенство в системе выполняется. Подставляя значение п=2 в уравнения системы, получаем систему: 11m+4k=30, 12m+5k=34, откуда k = m = 2. Ответ: По 2 самолёта каждого типа. Задача 12.Каждый зритель, пришедший на спектакль «королевский жираф», принёс с собой либо дохлую кошку, либо два кочана капусты, либо три тухлых яйца. После окончания спектакля оба артиста были с ног до головы закиданы припасами, причём на долю каждого досталось поровну попаданий. Правда король принял на себя лишь пятую часть всех яиц и седьмую часть капусты, но все 64 дохлые кошки полетели именно в него. Сколько зрителей пришло на представление? Решение: Из условия следует, что общее число кочанов капусты делится на 2, а общее количество яиц на 3. Пусть в короля попало x яиц и y кочанов(и 64 кошки), герцогу досталось 4х яиц и 6у кочанов. Так как всего в них угодило поровну предметов, то можно составить уравнение х+у+64=4х+6у, которое приводит к виду Зх+5у=64. Это уравнение имеет 4 решения в натуральных числах (их можно отыскать простым перебором): 1) x = 3, y = 11 2) x – 5, y = 8 3) х=13,у=5, 4) х = 18, у=2. Общее число яиц, очевидно, равно 5x, а общее число кочанов капусты 7у. Эти значения для каждого из четырёх случаев равны: 1) яиц – 15, кочанов- 77 2) яиц -40, кочанов - 56; 3) яиц -65, кочанов - 35; 4) яиц – 90, кочанов - 14 А теперь вспомним, что число яиц делится на 3, а число кочанов на 2. Из всех найденных ответов лишь последний удовлетворяет этим требованиям. Тогда число зрителей, принесших яйца, равно 90:3=30, число зрителей, запасшихся капустой, равно 14:2 = 7, а число зрителей, пришедших с кошкой, равно 64 (так как каждый принёс одну кошку). Поэтому общее число зрителей равно 30+7+64=101. Ответ: 101 зритель.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

 копеек, но не меньше
копеек, но не меньше  копеек, т. е. 29 < х < 33. Отсюда 319 < 11х < 363, следовательно, у Васи было не меньше 4 рублей. Но в этом случае у него осталось бы не меньше 37 копеек, а этого хватило бы еще на одну порцию мороженого, что противоречит условию. Итак, у Коли было 3 рубля, поэтому выполнены неравенства:
копеек, т. е. 29 < х < 33. Отсюда 319 < 11х < 363, следовательно, у Васи было не меньше 4 рублей. Но в этом случае у него осталось бы не меньше 37 копеек, а этого хватило бы еще на одну порцию мороженого, что противоречит условию. Итак, у Коли было 3 рубля, поэтому выполнены неравенства:  ≤ х <
≤ х <  , откуда 43 < х < 50.
, откуда 43 < х < 50. = 6 очков, а 6 не делится на 4. Таким образом, не существует команды, набравшей в турнире более 3 очков. Поэтому, если в турнире участвовало k команд, то общее число очков, набранных всеми командами, не должно превышать 3k. Поскольку в турнире было разыграно
= 6 очков, а 6 не делится на 4. Таким образом, не существует команды, набравшей в турнире более 3 очков. Поэтому, если в турнире участвовало k команд, то общее число очков, набранных всеми командами, не должно превышать 3k. Поскольку в турнире было разыграно  очков, то
очков, то  < 3k; k(k - 1) < 6k. И поскольку, очевидно, что k ≥ 4, то 4 ≤ k ≤ 7. следовательно, в турнире участвовало не более 7 команд.
< 3k; k(k - 1) < 6k. И поскольку, очевидно, что k ≥ 4, то 4 ≤ k ≤ 7. следовательно, в турнире участвовало не более 7 команд. х2 + у2+31,25. Из неравенства треугольника получаем z ≤ х + у. Тогда
х2 + у2+31,25. Из неравенства треугольника получаем z ≤ х + у. Тогда  х2 + у2 +31,25 ≤ 5х + 5у. Если умножить обе части этого неравенства на 4 и выделить полные квадраты, то получим (х - 10)2 + (2у - 5)5 ≤ 0. Но сумма квадратов чисел не может быть отрицательной, и последнее неравенство может быть истинным только при х = 10 и у =
х2 + у2 +31,25 ≤ 5х + 5у. Если умножить обе части этого неравенства на 4 и выделить полные квадраты, то получим (х - 10)2 + (2у - 5)5 ≤ 0. Но сумма квадратов чисел не может быть отрицательной, и последнее неравенство может быть истинным только при х = 10 и у = 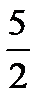 , когда левая часть равна правой. Тогда и неравенства
, когда левая часть равна правой. Тогда и неравенства  пути между А и В, он оглянулся и заметил, что от остановки С, непосредственно предшествующей остановке А, к остановке А отошел трамвай. Расстояния АВ и СА соответственно равны 1 км и 1,5 км, а скорость трамвая равна 30 км/ч. С какой скоростью должен бежать пассажир, чтобы успеть сесть в трамвай, независимо от того, побежит он к остановке А или к остановке В? [2, с.168-169]
пути между А и В, он оглянулся и заметил, что от остановки С, непосредственно предшествующей остановке А, к остановке А отошел трамвай. Расстояния АВ и СА соответственно равны 1 км и 1,5 км, а скорость трамвая равна 30 км/ч. С какой скоростью должен бежать пассажир, чтобы успеть сесть в трамвай, независимо от того, побежит он к остановке А или к остановке В? [2, с.168-169]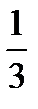 υ ч, а до остановки В —
υ ч, а до остановки В —  υ ч. До остановки А трамвай затратит времени
υ ч. До остановки А трамвай затратит времени  =
=  ч, а до остановки
ч, а до остановки  =
=  ч. Так как в обоих случаях пассажир должен прибежать на остановку не позднее трамвая, то получим:
ч. Так как в обоих случаях пассажир должен прибежать на остановку не позднее трамвая, то получим: км/ч, а из второго — υ ≥ 8 км/ч. Пассажир должен успеть добежать до любой остановки, поэтому υ ≥ 8 км/ч.
км/ч, а из второго — υ ≥ 8 км/ч. Пассажир должен успеть добежать до любой остановки, поэтому υ ≥ 8 км/ч. Геометрическая интерпретация неравенств этой системы приведена на рисунке. Из него видно, что надо проверить, удовлетворяют ли первому уравнению системы только три пары n = 4, m = 1; n = 4, m = 2 и n = 5, m = 1.
Геометрическая интерпретация неравенств этой системы приведена на рисунке. Из него видно, что надо проверить, удовлетворяют ли первому уравнению системы только три пары n = 4, m = 1; n = 4, m = 2 и n = 5, m = 1. , m <
, m <  , т.е. n ≥ 3, m ≤ 4. В принципе, уже можно начинать перебирать значения m = 0, 1, 2, 3 и 4, но мы продолжим искать ограничения. Условие n + m < 7 означает, что m + n ≤ 6. Так как m > 0, то из этого непосредственно следует, что n ≤ 5. Укажем еще более строгое ограничение.
, т.е. n ≥ 3, m ≤ 4. В принципе, уже можно начинать перебирать значения m = 0, 1, 2, 3 и 4, но мы продолжим искать ограничения. Условие n + m < 7 означает, что m + n ≤ 6. Так как m > 0, то из этого непосредственно следует, что n ≤ 5. Укажем еще более строгое ограничение. .
.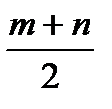 ≥ 2.Следовательно, n ≥ 6 - 2 = 4, т.е. n ≥ 4.
≥ 2.Следовательно, n ≥ 6 - 2 = 4, т.е. n ≥ 4. = 5.
= 5. = 45 матчей разыграно не более трех очков, поэтому общее число не более 45∙3 = 135. Таким образом, 10х + 9 ≤ 135 <=> 10х ≤ 126 <=> х ≤ 12,6. А так как х – целое число, х ≤ 12. Следовательно, наибольшее число очков, которые могла набрать команда, занявшая последнее место, 12.
= 45 матчей разыграно не более трех очков, поэтому общее число не более 45∙3 = 135. Таким образом, 10х + 9 ≤ 135 <=> 10х ≤ 126 <=> х ≤ 12,6. А так как х – целое число, х ≤ 12. Следовательно, наибольшее число очков, которые могла набрать команда, занявшая последнее место, 12. . Величина
. Величина  должна быть целым числом, большим 1. Это возможно лишь при t = 3 или t = 4. В первом случае п = 8, во втором п = 6. В обоих случаях количество деталей, которое составляет заказ, равно n t = 24.
должна быть целым числом, большим 1. Это возможно лишь при t = 3 или t = 4. В первом случае п = 8, во втором п = 6. В обоих случаях количество деталей, которое составляет заказ, равно n t = 24.


