
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра математики и методики преподавания математикиСтр 1 из 18Следующая ⇒
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ МАКСИМА ТАНКА КАФЕДРА МАТЕМАТИКИ И МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА Конспект лекций. Алгебра Разработчики: Доценты кафедры М.И.Лисова, О.Н.Пирютко, Старший преподаватель кафедры И.А.Ананич
Минск 2010
Полная и неполная индукции. Метод математической индукции План Введение 1. Индукция и дедукция как методы мышления. Полная и неполная индукции. 2. Метод математической индукции. 3. Применение метода математической индукции в различных разделах математики.
Введение Элементарная математика – раздел математики, объектом изучения которого служат понятия школьного курса математики. Но поскольку школьные программы разнообразны, то само понятие элементарной математики несколько не определено и размыто. Э.м. включает в себя методы и задачи, в которых не пользуются общими понятиями переменной, предела, множества, т.е. включает такие предметы как арифметику, элементарную теорию чисел, элементарную алгебру и геометрию. Э.М. иногда характеризуют как математику постоянных величин, однако это не так, в элементарной математике рассматривают не только постоянные, но и переменные величины (например, тригонометрические функции), но в элементарной математике речь идет, как правило, о конкретных функциях. Общее понятие предела, кривой, поверхности, фигуры выходят за рамки элементарной математики. Целые числа. Делимость целых чисел. Признаки делимости План 1. Множество целых чисел. Свойства и операции. 2. Теоремы о делимости. 3. Деление с остатком.
Множество целых чисел – это натуральные, им противоположные и ноль. Свойства целых чисел (Z). 1. Множество целых чисел замкнуто относительно операций сложения, вычитания, умножения: это значит, что результат указанных операций над целыми числами так же принадлежит множеству целых чисел. 2. Дискретно: для любого целого числа можно указать следующее за ним, между двумя соседними целыми числами нет целого числа. 3. Упорядоченно: для любых целых чисел можно установить отношение порядка (a>b, a<b, a=b). Свойства операций с целыми числами
1. a + b = b + a (коммутативный закон сложения)
2. (a + b) +с = a + (b +c) (ассоциативный закон сложения) 3. a - a = 0 4. a + 0 = a 5. a b = b a (коммутативный закон умножения) 6. (a b) с = a (b c) (ассоциативный закон умножения) 7. (a + b) с = a с + b c (дистрибутивный закон умножения относительно сложения) 8. 1·a = a Определение Если a: b = с Теорема о единственности разложения натурального числа на простые множители.(Основная теорема арифметики). Существует и при том единственное разложение всякого натурального числа (кроме 1) на простые множители. Представление натурального числа в виде n = p1, p2, p3, … pn – простые числа, называется каноническим разложением натурального числа на простые множители. Например, 36 = 3222, 195=31·51·131. Задача Сколько всего делителей имеет натуральное число, если его каноническое разложение имеет вид n = Пример 60 = 223151
Его делители 1, 2, 3,4, 5, 6, 10, 12,15,20, 30, 60 – всего 12. Как подсчитать число делителей, не перечисляя их? Число вариантов(способов) вхождения в делители данного числа делителя с основанием 2 всего три: 1- совсем нет такого делителя, 2- 21 3- 22 Число вариантов(способов) вхождения делителя с основанием 3 всего 2 1- совсем нет такого делителя, 2- 31. Число вариантов(способов) вхождения делителя с основанием 5 всего 2 1- совсем нет такого делителя, 2- 51. Каждый из первых трех вариантов можно объединить с каждым из двух вторых, всего получится 3·2=6. Каждый из этих 6 вариантов можно объединить с любым из двух способов вхождения числа 5 в делители данного числа, всего получится 3·2·2= 12. Аналогичное этому доказательство в общем виде приводит к результату: Количество всевозможных делителей числа n = (α1+1)(α2+1) (α3+1)…(αn+1).
Доказательство Предположим, что p – наибольшее простое число. Рассмотрим число 2·3·5·…· p + 1- это число либо само простое, большее p, либо делится на простое число, не содержащееся среди чисел 2, 3, 5, …,p, а следовательно, большее p. Получили противоречие, доказывающее теорему.
Связь между НОД и НОК. О бозначим НОД(а; b) = d, НОК(a;b) = m.
Так как НОД(а; b) = d, то a = a1d, b = b1d, (a1;b1)=1.
Так как НОK(а; b) = m, то m = a1·d· b1, тогда а·b = a1·d· b1·d = m d. Таким образом, НОД(а;b) ·НОК(a;b) = ab.
Теоремы о делимости 1.Если a: m, b: m, то (a +b): m, (a -b): m.
2. Если a: m, b: n, то a b: mn. 3. Если a: m, an: mn. 4. Если сумма нескольких слагаемых делится на m и известно, что все слагаемые, кроме одного, делятся на m, то и оставшееся слагаемое делится на m. 5. Если хотя бы один из множителей произведения делится на m, то и произведение делится на m.
Пример Докажите, что произведение n(n+1)(n+2) делится на 6 при любом натуральном n. Доказательство Если n – нечетное, то n +1 – четное, следовательно, произведение делится на 2. Если n – не кратно 3 (значит при делении на 3 дает остаток 1 или 2), то n +2 или n + 1 кратно 3. Таким образом, произведение n(n+1)(n+2) делится на 2 и на 3, а так как эти числа взаимно простые, то оно делится на 6.
Признаки делимости 1.Для того, чтобы натуральное число делилось на 3(9) необходимо и достаточно, чтобы сумма цифр этого числа делилась на 3(9). 2. Для того, чтобы натуральное число делилось на 11 необходимо и достаточно, чтобы разность между суммой цифр этого числа стоящих на четных местах и суммой цифр этого числа стоящих на нечетных местах делилась на 11. 3. Для того, чтобы натуральное число делилось на 4 необходимо и достаточно, чтобы число, образованное двумя последними цифрами этого числа делилось на 4. Докажем 2. p= an10n + an-110n-1 + an-210n-2 +…..+ a1101+ a0 = an (11-1)n + an-1 (11-1)n-1 + an-2 (11-1)n-2 +…..+ a1 (11-1)1+ a0 = 11K + (an (-1)n + an-1 (-1)n-1 + an-2 (-1)n-2 +…..+ a1 (-1)1+ a0). Если число p делится на 11, то второе слагаемое (an (-1)n + an-1 (-1)n-1 + an-2 (-1)n-2 +…..+ a1 (-1)1+ a0) суммы делится на 11 и обратно: для того, чтобы число p делилось на 11, достаточно, чтобы это слагаемое делилось на 11. Второе слагаемое суммы в зависимости от четности или нечетности n равняется (an - an-1 + an-2 -…..-a1 + a0) или (-an+an-1 - an-2 +…..-a1 + a0), т.е. представляет собой разность между суммой цифр этого числа, стоящих на четных местах и суммой цифр этого числа, стоящих на нечетных местах. 4. Если число делится на 1001, то оно делится на 7, 11, 13.
Деление с остатком
Доказательство Пусть b > 0. Рассмотрим ряд чисел: …-2b, -1b,0b, 1b, 2b,… В этой последовательности найдется наибольшее число, которое не превосходит a, т.е. b· q ≤ a < b· (q +1) или 0≤ a - b· q < b. Обозначим a - b· q = r, получим: a = b· q + r, где 0≤ r <│b│, что и требовалось доказать. Случай b ≤ 0 доказать самостоятельно. Единственность
Евклида. По теореме о делении с остатком для любых натуральных чисел a и b справедливо равенство a = b· q + r, где 0≤ r < b. Если d =(a;b), то по теореме 4 о делимости d =(r;b), тогда по теореме о делении с остатком для натуральных чисел r и b справедливо равенство: b = r· q + r1, где 0≤ r1 < r, d =(r;r1), далее r= r1· q + r2, где 0≤ r2 < r, d =(r2; r1), r1= r2· q + r3, где 0≤ r2 < r, d =(r2; r3), ………………………………………….. rn-1= rn· q, d =(rn-1; rn) = rn Поскольку остатки при делении уменьшаются, то на каком-то шаге появится остаток, равный нулю. rn-1= rn· q, d =(rn-1; rn) = rn
Tаким образом, наибольший общий делитель двух чисел равен последнему, отличному от нуля остатку при делении по алгоритму Евклида.
Пример Найти (899; 493) = 29 899│ 493 493 1 493│ 406 406 1 406│ 87 348 4 87│ 58 58 1 58│ 29 58 2 Применение теоремы о делении с остатком. Множество целых чисел можно разбить на классы, в зависимости от остатков при делении целых чисел на некоторое данное натуральное число. Вообще при делении на число b могут быть остатки:
0, 1,2,3…, b-1. Пример Докажите, что ни при каком целом n число n2 +1 не делится на 3. Разобьем множество целых чисел на классы, в зависимости от остатков при делении на 3. Если число имеет вид 3к, то n2 +1= 9k2 +1 – не делится на 3. Если число имеет вид 3к + 1, то n2 +1= 9k2 + 6k +2 – не делится на 3. Если число имеет вид 3к + 2, то n2 +1= 9k2 + 12k +5 – не делится на 3. Таким образом, число n2 +1 не делится на 3. Литература 1.Ананченко К.О. Алгебра – 8 - Мн.,2002 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Литература 1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000 Иррациональные уравнения. Иррациональными называются уравнения и неравенства, содержащие переменную под знаком корня или под знаком возведения в дробную степень. Все корни чётной степени, входящие в уравнение, являются арифметическими, т.е. если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то значение корня положительно. Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения. Основные методы решения иррациональных уравнений: 1. возведение обеих частей уравнения в одну и ту же степень; 2. замена переменной; 3. умножение обеих частей уравнения на одну и ту же функцию; 4. применение свойств функций, входящих в уравнение. Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например возведение обеих частей уравнения в чётную степень, приводят к уравнению-следствию. Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения. Возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в чётную степень.
Рассмотрим несколько примеров.
Пример 1. Решим уравнение Решение. Возводим обе части уравнения в квадрат, получаем:
Проверка показывает, что только Ответ: -4.
Пример 2. Решим уравнение
Решение. Выполним замену. Обозначим: Тогда Исходное уравнение принимает вид:
Полученное уравнение равносильно системе:
Из получившейся системы, имеем: Возвращаемся к подстановке, получаем:
Ответ: 1; Пример 3. Решим уравнение Решение: Пусть Тогда имеем:
Откуда последовательно получаем:
Возвращаясь к первоначальным подстановкам, получим:
Откуда С помощью проверки убеждаемся, что оба корня являются корнями исходного уравнения.
Ответ: 1; -15. Пример 4. Решим уравнение Решение: Рассмотрим функцию Исходное уравнение принимает вид:
Ответ: 5.
Иррациональные неравенства. Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т.д. Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению: 1) Неравенство вида
2) Неравенство вида 3) Неравенство вида 4) Неравенство вида
Пример 5. Решим неравенство
Решение. Введём новую переменную
Решая это неравенство и возвращаясь к исходным переменным, получаем: Ответ: Пример 6. Решим неравенство
Решение: Перепишем неравенство в виде: Это неравенство равносильно системе неравенств:
Пример 6. Решим неравенство Решение: Рассмотрим функцию Ответ: нет решений. Литература 1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999 2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Текстовые задачи План ЛИТЕРАТУРА 1. 3000 конкурсных задач по математике /Под ред. проф. Н.А.Бобылева. - М.: Рольф, 1997. 2. Азаров А.И., Барвенов С.А., Федосенко B.C. Текстовые задачи. - Мн.: Аверсэв, 2005. 3. Азаров А.И., Барвенов С.А., Федосенко B.C., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи.- Мн.: ТетраСистемс, 1998.
4. Барабанов Е.А., Воронович И.И., Каскевич В.И., Мазаник С.А. Задачи районного тура Минской городской математической олимпиады школьников. – Мн., Фаритекс, 2002. 5. Бахтина Т. П. Готовимся к олимпиадам, турнирам и математическим боям. Математикон 8. - Мн.: Аверсэв, 2003. 6. Габринович В.А., Громак В.И. Решим любую задачу. Задачи на экзаменах по математике в БГУ в 1995 году с решениями и комментариями: учеб пособие. - Мн.: Белгосуниверситет, 1996. 7. Кипнис И.М. Задачи на составление уравнений и неравенств. - М.: Просвещение, 1980. 8. Лурье М.В. Задачи на составление уравнений. Техника решения. - М.: УНЦ ДО, 2004. 9. Лурье М.В., Александров Б.И. Задачи на составление уравнений. - М.: Наука, 1990. 10. Мельников И.И., Сергеев И.Н. Как решать задачи по математике на вступительных экзаменах. - М.: Изд-во Моск. ун-та, 1990. 11. Фарков А.В. Математические олимпиады в школе 5 – 11 классы. - М.: Айрис пресс, 2003.
Показательные неравенства. Решение показательных неравенств вида
Теорема 1. Если Теорема 2. Если
Рассмотрим несколько примеров.
Пример 7. Решим неравенство Решение. Так как
решением которого является интервал (-1;7)
Ответ: (-1;7)
Пример 8. Решим неравенство
Решение. Последовательно получаем:
Решаем полученное неравенство методом интервалов и получаем:
Пример 9. Решим неравенство
Решение. Перепишем неравенство в виде Разделим обе части неравенства на
Обозначим
Ответ:
Графики функций и уравнений План 1. Простейшие преобразования графиков функций Школьной математики
Задачи с параметрами В зависимости от того, какая роль отводится параметру в задаче (неравноправная или равноправная с переменной), можно соответственно выделить два основных графических приема: первый – построение графического образа на координатной плоскости (x; y), второй – на (x; a). Задача 5. Найти все значения параметра а, при которых уравнение Решение. Переходя к логарифмам по основанию 5, получаем уравнение Построим графики функций
Рис. 16 Ответ: Задача 6. При каких значениях a система уравнений не имеет решений? Решение. Система На рис. 21 точка (3; 0) – центр поворота. Ясно, что если прямая семейства Важно при записи ответа не упустить, что существует еще одна прямая семейства, а именно у = – х + 3, проходящая через «дырки» в гиперболе. Поэтому при а = –1 система также не имеет решений.
Рис. 17 Ответ: а = –1 или Задача 7. При каких значениях параметра а уравнение Решение. Рассмотрим функции у = ах и
иметь одно решение, получим а =
Рис. 18 Итак, прямые семейства у = ах имеют с дугой АВ только одну общую точку при Ответ: Литература 1. Архипов Б.М., Мазаник А.А., Петровский Г.Н., Урбанович М.И. Элементарные функции – Мн: Вышэйшая школа, 1991. 2. Бахтина Т. П. «Таблетки» и «компрессы» при построении графиков. // Математика в школе. – 2004 – №8. 3. Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики. – М.:МЦНМО, 2001. 4. Ершов Л.В., Райхмист Р.Б. Построение графиков функций – М.: Просвещение, 1984. Неравенств и их систем План 1.Функциональный подход в новых тенденциях школьного математического образования. 2.Теоретическое обоснование методов функционального подхода. 3. Система задач на применение функционального подхода.
1. Функциональный подход в новых тенденциях школьного математического образования.
На современном этапе развитие образования поставило ряд проблем, которые касаются выбора стратегии образования, интеграции образовательных систем, поиска оптимальных моделей обучения, адекватных завтрашнему дню. Одной из проблем, выдвинутых сменой парадигмы современного образования является проблема оптимального соединения в моделях образования блоков естественнонаучных, социально-гуманитарных и профильных знаний. Перспективным в этом смысле является поиск межпредметных связей, интегрирование дисциплин, для реализации современных тенденций школьного образования: гуманизации, гуманитаризации, дифференциации обучения, внутрипрофильной и межпрофильной интеграции, алгоритмизации поиска решения задач необходимы новые требования к содержанию и методам школьного курса математики, связанные с выработкой у учащихся навыков исследовательско - поисковой деятельности, осуществление обучения как моделирования процесса открытия новых знаний. «Слово «гуманизм» происходит от латинского — человечный. Гуманизация образования предполагает «очеловечивание» знаний, т.е. такую организацию учебного процесса, при котором знания имеют для ученика личностный смысл, сам ученик «не теряется» в процессе его обучения. Чтобы «не терять» ученика, надо знать его индивидуальные особенности и учитывать их в процессе обучения». Слово “гуманитарный” происходит от латинского слова, означающего духовная культура. Следовательно, смысл гуманитаризации образования заключается в приобщении ученика к духовной культуре, творческой деятельности, методологии открытия нового. Гуманитаризация образования предполагает вооружение школьников методами научного поиска, среди которых эвристические приемы в методы научного познания другими словами, гуманитаризация образования призвана создать условия, побуждающие ученика к активной творческой деятельности и обеспечивающие его участие в ней. Анализ конкурсных задач на вступительных экзаменах в ВУЗы, задач, предлагаемых на различных олимпиадах, турнирах показывает, что задания, которые они содержат, требуют навыков исследовательско - поисковой деятельности, функционального видения математических объектов, явлений, процессов. Анализ программ по математике для классов различных профилей показывает, что изменение количества часов, структуры курса математики, целей обучения приводит к необходимости рассмотрения общего принципа, объединяющего различные виды программ, дающего возможность восприятия математических знаний как чего-то цельного, а не механически соединяемых отдельных тем курсов алгебры и геометрии. Изменения в структуре и содержании предъявляемых систем знаний должны отвечать требованиям гуманизации школьного образования, обеспечивающим оптимальное умственное развитие всех учеников, к какой бы группе они ни принадлежали. Очевидно, что недостаточно деления всех заданий на варианты для “слабых”, для “сильных”, для “средних”. Предлагаемые задачи, упражнения, теоретические сведения должны быть объединены общей идеей исследовательско - поисковой деятельности учащихся, интеграционным процессом внутри предмета и между однопрофильными курсами. Гуманизация обучения направлена на формирование таких приемов, подходов к решению задач, которые придают обучению характер творческого поиска на различных уровнях: от эмпирического, реализуемого на иллюстрациях и моделях, до теоретического обоснования и исследования. Выше сказанное позволяет сделать вывод о перспективах функционального подхода при изучении математики. Под общим функциональным подходом понимается организация деятельности учителя и учащихся, направленная на формирование общих и специфических приемов мышления на основе функционального представления объектов и явлений. Основу функционального подхода к изучению математики с точки зрения фактических знаний, составляет использование свойств всех изучаемых в школе функций, как средства интеграции различных тем и однопрофильных курсов, и с точки зрения способов мышления — развитие творческого мышления. Очевидно, что для реализации идеи общего функционального подхода необходимо сформировать у учащихся умение функционального видения объектов, умение рассматривать математические объекты и связи между ними в динамике изменения определяющих их параметров. Этот процесс поэтапного формирования функционального мышления представляется возможным и необходимым не только на алгебраическом материале, но и на геометрическом. Задачи, требующие для решения развитого функционального мышления, занимают все более прочное место в экзаменационных заданиях. Доказательство. Так как х0 - корень, то f(х0)=g(х0). Если х<х0, то f(х)<f(х0) поскольку f (х) - возрастающая функция, а g(х)> g(х0) в силу того, что она является убывающей. Значит, f(х) < g(х), и на множестве х<х0 уравнение f (х)= g (х) не имеет решений. Если х>х0, то f(х)>f(х0), а g(х)< g(х0), поскольку f, g - монотонные функции. Следовательно, f(х)>g(х) и уравнение f(х)=g(х) не имеет решений на множестве х> х0. Итак, х0 - единственный корень.
Следствие. Если f(х) - возрастающая на множестве М функция, g (х) - убывающая и уравнение f(х)=g(х) имеет на множестве М решение х0, то решением неравенства f(х) > g (х) являются все хÎМ такие, что х>х0, а решением неравенства f (х)< g(x) - все х Î М такие, что х< х0.
Теорема 2. Если f (х) - возрастающая (убывающая) на множестве М функция, то уравнение f(х)=С, где С - некоторое действительное число, имеет не более одного решения на множестве М.
Теорема 3. Если f(х) - возрастающая (убывающая), непрерывная функция на отрезке [a, b], то f (х) принимает все значения между f (а) и f (b), причем каждое из них лишь при одном x Î [a;b]. Следствие. Если f(х) возрастающая (убывающая), непрерывная функция на отрезке [a;b] и f(a)f(b)<0, то существует, причем единственное, решение уравнения f (х)=0 на (а;b).
Теорема 4. Если f(х) - возрастающая (убывающая) функция, определенная на всей числовой прямой, то уравнения f(g(х)) = f(h(х)) и g(х)=h(х) - равносильны.
Монотонность в условии теоремы 4 нужна, чтобы не происходило потери корней при переходе к уравнению g(х)= h(х). А функция f должна быть определена на всей числовой прямой, чтобы не было приобретения корней при переходе к уравнению g(х)= h(х). Даже если f(х) определена не при всех х ÎR, то посторонние корни, которые могут появиться при переходе к уравнению-следствию g(х)= h(х), затем обычно легко отсеять проверкой.
Замечание 1. Если f (х) - возрастающая (убывающая) функция на ОДЗ переменной уравнения f(g(х))= f(h(х)), то последнее уравнение равносильно уравнению g(х)= h(х) на множестве допустимых значений переменной х.
Замечание 2. Если f (х) является четной и возрастает (убывает) при х≥0, то f(g(х))= f(h(х)) • Теорема 5. Если f (х) - возрастающая на множестве М функция и при любом х Î М значение функции принадлежит М, то уравнения f(f(х))=х и f(х)=х равносильны. Доказательство. Пусть х0 - корень уравнения f(х)=х, т. е. f (х0)=х0. Докажем, что х0 является корнем уравнения f (f (х0)=х. Так как f(f(х0)= f(х0)=х, то f(f(х0)=х0, а это значит, что х0 - корень уравнения f(f(х)= = х. Докажем обратное. Пусть х0 - корень первого уравнения, т. е. выполнено равенство f(f(х0)= х0. Предположим, что х0 не является корнем второго уравнения. Пусть для определенности f(х0)< х0 Тогда, т. к. f(х) возрастает, получаем f(f(х0)< f (х0)< х0, что противоречит тому, что f(f(х0)= х0. Аналогично проводится рассуждение, если f(х0)> х0, и тоже приходим к противоречию. То есть методом от противного доказали, что f(х0)= х0.
Следствие 1. Если f (х) - возрастающая на множестве М функция, то f(f(f(.. ff(х)))...)=х • f(х) =х.
Следствие 2. Если f(х) возрастает на своей области определения, то f(х)=х • f(f(f(.. ff(х)))...)=х. Замечание 1. Если функция f (х) не является возрастающей, то уравнения f (f (х))=х и f (х)=х не равносильны. В этом случае f (f (х))=х
На ограниченности функций Пример 1. Решить уравнение
Решение. Оценим правую часть уравнения
Но значение выражения в левой части исходного уравнения:
Ответ: Æ. Пример 2. Имеет ли корни уравнение Решение. Запишем данное уравнение в виде Ответ: не имеет.
Пример 3. Найти все значения параметра а при которых уравнение 3х4 – 4х3 +12х2 +а =0 имеет корни?
Решение. Рассмотрим функцию f(x) = 3х4 – 4х3 +12х2. Выделим полный квадрат f(x) = х2
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.140 (0.214 с.) |
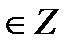 , то a называется кратным b, а b – делителем числа a.
, то a называется кратным b, а b – делителем числа a. , где
, где .
.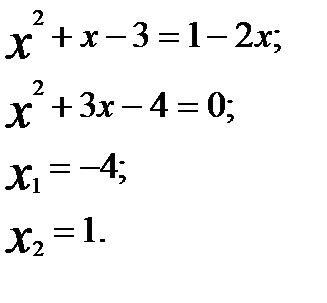
 является корнем исходного уравнения.
является корнем исходного уравнения.
 заметим, что
заметим, что  .
. и
и 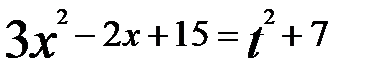 .
.
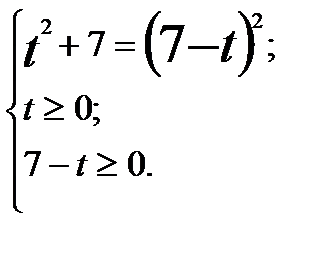
 .
.
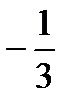 .
. .
.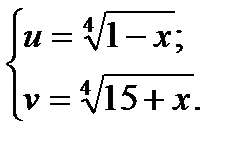




 .
. .
.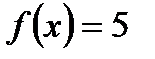 .
. . Функция
. Функция 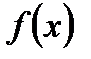 монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что
монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что 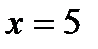 является корнем уравнения.
является корнем уравнения. равносильно системе
равносильно системе
 равносильно неравенству
равносильно неравенству  .
. равносильно совокупности систем
равносильно совокупности систем 
 равносильно системе
равносильно системе
 .
.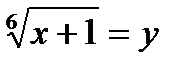 . Тогда исходное неравенство принимает вид:
. Тогда исходное неравенство принимает вид: .
. .
. .
.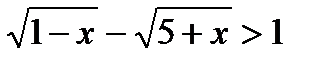 .
. .
. Откуда получаем
Откуда получаем  .
. .
. . Область определения этой функции
. Область определения этой функции  . Функция
. Функция  возрастает на всей области определения, причём
возрастает на всей области определения, причём 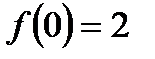 . Значит, неравенство
. Значит, неравенство 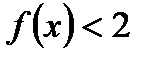 решений не имеет.
решений не имеет. , где
, где  , основано на следующих теоремах:
, основано на следующих теоремах: то неравенство
то неравенство  равносильно неравенству
равносильно неравенству 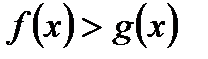 .
. , то неравенство
, то неравенство  равносильно неравенству
равносильно неравенству  .
. .
. , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству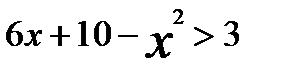 ,
, .
.



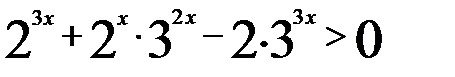 .
. . Так как
. Так как  , получаем
, получаем .
. и получаем неравенство
и получаем неравенство  , из которого имеем
, из которого имеем  . Последовательно получаем:
. Последовательно получаем:


 имеет решение.
имеет решение. , которое равносильно уравнению
, которое равносильно уравнению 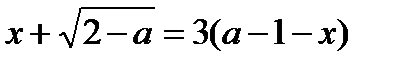 (1), если выполняется условие
(1), если выполняется условие 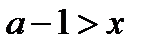 (2). Выражая x из равенства (1) и подставляя в неравенство (2), получаем неравенство
(2). Выражая x из равенства (1) и подставляя в неравенство (2), получаем неравенство 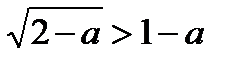 (3). Чтобы решить это неравенство, решим сначала уравнение
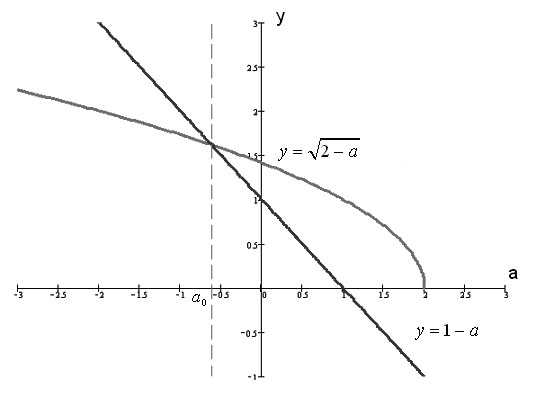
(3). Чтобы решить это неравенство, решим сначала уравнение  .
. и
и  (рис. 20). Тогда
(рис. 20). Тогда  – есть решение этого уравнения. Так как мы решаем неравенство
– есть решение этого уравнения. Так как мы решаем неравенство  , тогда решение неравенства
, тогда решение неравенства  .
.

 равносильна исходной.
равносильна исходной. вращается внутри угла OMA, то система не имеет решений. Устанавливаем, что угловой коэффициент прямой MA равен
вращается внутри угла OMA, то система не имеет решений. Устанавливаем, что угловой коэффициент прямой MA равен 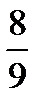 . Тогда при таком повороте параметр a принимает все значения из промежутка (–
. Тогда при таком повороте параметр a принимает все значения из промежутка (–  ; 0]. Заметим, что мы включили a = 0, поскольку прямая MO не пересекает гиперболу.
; 0]. Заметим, что мы включили a = 0, поскольку прямая MO не пересекает гиперболу.
 .
. имеет единственное решение?
имеет единственное решение? . График второй функции легко построить, рассмотрев уравнение (у – 1)2 = 8х— х2 — 15 при у ≥ 1. Преобразовав последнее к виду (у – 1)2 + (х – 4)2 = 1, получаем, что искомый график — полуокружность с центром (4; 1) и радиусом 1. На рис. 22 это дуга АВ. Все прямые у = ах, проходящие между лучами OA и ОВ пересекают дугу в одной точке. Также одну точку с дугой имеют прямая ОВ и касательная ОМ. Легко показать, что угловые коэффициенты прямых ОВ и OA соответственно равны
. График второй функции легко построить, рассмотрев уравнение (у – 1)2 = 8х— х2 — 15 при у ≥ 1. Преобразовав последнее к виду (у – 1)2 + (х – 4)2 = 1, получаем, что искомый график — полуокружность с центром (4; 1) и радиусом 1. На рис. 22 это дуга АВ. Все прямые у = ах, проходящие между лучами OA и ОВ пересекают дугу в одной точке. Также одну точку с дугой имеют прямая ОВ и касательная ОМ. Легко показать, что угловые коэффициенты прямых ОВ и OA соответственно равны 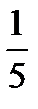 и
и  . Устанавливаем, что угловой коэффициент касательной ОМ равен
. Устанавливаем, что угловой коэффициент касательной ОМ равен  , причем это можно сделать не обязательно при помощи производной. Действительно, потребовав от системы
, причем это можно сделать не обязательно при помощи производной. Действительно, потребовав от системы

 на ОДЗ переменной х.
на ОДЗ переменной х. f(х)=х, т. е. все корни уравнения f(х) = х являются корнями уравнения f(f(х))=х.
f(х)=х, т. е. все корни уравнения f(х) = х являются корнями уравнения f(f(х))=х.
 =
=  .
. . Таким образом, т. к. левая часть строго меньше
. Таким образом, т. к. левая часть строго меньше  , а правая – больше или равна
, а правая – больше или равна 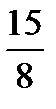 , исходное уравнение решений не имеет.
, исходное уравнение решений не имеет. ?
? . Рассмотрим функцию f(x) =
. Рассмотрим функцию f(x) =  . Так как f(x) =
. Так как f(x) =  , а правая часть преобразованного уравнения отрицательна, то исходное уравнение корней не имеет.
, а правая часть преобразованного уравнения отрицательна, то исходное уравнение корней не имеет.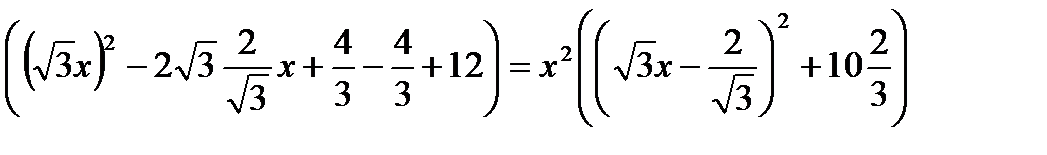 .
.


