Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи с альтернативным условиемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Условие задач может быть сформулировано таким образом, что при составлении одного из уравнений возникает альтернатива: уравнение записывают по-разному, и нужно рассматривать несколько вариантов. Заметим, что в других разделах элементарной математики задачи, для решения которых необходимо рассматривать несколько возможных вариантов, не так уж редки. Например, при решении уравнений или неравенств с модулями приходится рассматривать случаи, когда выражения, стоящие под знаком модуля, положительны (или равны нулю) и когда они отрицательны. При решении логарифмических неравенств исследуются случаи, когда основания входящих в задачу логарифмов больше или меньше единицы, и т. д. В таких случаях каждая из таких задач требует рассмотрения всех возможных вариантов, и решение находится лишь после того, как все эти возможности будут исследованы. Задача 13.Имеются три несообщающихся между собой резервуара, причем объем третьего не меньше объема второго. Первый резервуар имеет объем V и может быть заполнен первым шлангом за 3 часа, вторым за 4 часа, а третьим за 5 часов. К каждому из резервуаров можно подключить любой из этих шлангов. После того, как произведено подключение к каждому из резервуаров по одному шлангу каким-либо способом, все шланги одновременно включаются. Как только какой- то резервуар наполняется, соответствующий шланг отключается и не может быть подключен в дальнейшем к другому резервуару. При самом быстром способе подключения заполнение окончится через 6 часов. Если бы резервуары сообщались, то заполнение окончилось бы через 4 часа. Найдите объемы второго и третьего резервуаров(v2 и v3). Решение:Пусть x, y, z - производительности первого, второго и третьего шланга соответственно. Известно, что Так как сообщающиеся резервуары наполняются за 4 ч, то 4( v2+v3= Т.к. первый резервуар не наполняется никаким шлангом за 6ч, то либо v2 либо v3 заполняется за 6 ч каким-либо шлангом. Т. к. Тогда либо v3=6x=2v, v2= Ответ: v2 = Задача 14. В бассейн проведены две трубы разнойпропускной способности. Первая из труб расположена на боковой стене, а вторая — на дне бассейна. Обетрубы могутработать на сливи на наполнение. Пропускная способность каждой трибы при переходе от наполнения к сливу не меняется и не зависит от уровня воды над ней. Перваятруба работает на слив лишь тогда, когда уровень воды выше уровня расположения ее входа. Бассейн наполнили на Решение:Исходя из условия задачи нельзя сказать сразу, находится ли вход в первую трубу выше 1/4 высоты бассейна или он ниже этого уровня. В то же время первое условие задачи (первую трубу включили на слив, а вторую—на наполнение) приводит в каждом из возможных случаев расположения входа первой трубы к разным уравнениям. Для того чтобы найти решение, необходимо рассмотреть оба возможных варианта.
I случай: х < h/4.Здесь h —высота бассейна, х— уровень расположения входа первой трубы. Обозначим пропускные способности труб буквами v 1 и v2, соответственно, а площадь дна бассейна примем равной 1, Тогда имеем систему уравнений:
Эта система уравнений фактически содержит только две неизвестные величины:
Решая эту систему, находим неизвестные:
Неравенство х<h/4показывает, что в рассмотренном случае отношение x/h меньше 1/4. Поэтому решение x/h=169/288 не удовлетворяет условиям задачи. II случай: х
Преобразуя эту систему так же, как и в предыдущем случае получим два уравнения для определения двух неизвестных Поскольку в данном случае х Ответ:В3 раза.
Задача 15. Из города А в город В, расстояние между которыми 200 км, мотоциклист ехал 6 часов. Сначалаон двигался со скоростью v1, превышающей 12 км/ч, а потом со скоростью v2, причем время движения с каждой скоростью пропорционально этой скорости. Через 4 часа послевыезда мотоциклист был в120 км от города А. Определитьскорости v1 и v2 . Решение. Время движения мотоциклиста со скоростью v1 обозначим через t1, а со скоростью v2 - через t2. Тогда условие задачи приводит к трем уравнениям для четырех неизвестных: v1 t1+ v2 t2=200, t1+ t2=6,
Однако четвертое уравнение в этой задаче сразу составить нельзя. Не ясно, то ли 120 км были пройдены за 4 часа со скоростью v1, то ли движение на этом пути происходило с той и другой скоростью. Поэтому необходимо рассмотреть два случая. I случай. Если t1 4 v1 =120, т.е. v1 =30 км/ч. II случай. Если t1<4, то четвертое уравнение таково: v1 t1+(4- t1) v2 =120, и от сюда с учетом первого и второго уравнений имеем v2 =40 км/ч. Разберем первый случай: v1 =30 км/ч, тогда
Исключив t2 и v2 из первых трех уравнений системы, получаем для v1 уравнение 3t Один из корней этого уравнения меньше 4, другой корень не подходит, поскольку он больше 6, и, значит, такой случай отпадает. Во втором случае (v2 =40 км/ч) имеем смешанную систему: Из этой системы находим v1 = 20км/ч, t1=2<4 Ответ: v1 = 20км/ч, v2 = 40 км/ч. Задача 16. Из пункта А одновременно выходят три пешехода и одновременно возвращаются в тот же пункт, обойдя маршрут, состоящий из прямолинейных отрезков АВ, ВС, СD, DA, которые образуют равнобедренную трапецию (АВ, BC-боковые стороны). На указанных отрезкахскорости всех пешеходов постоянны и равны: у первого 6, 8, 5 и 8 км/ч соответственно, у второго – 7, 7, 6, и 8 км/ч соответственно. Скорость третьего пешехода на каждом из отрезков равна либо 7км/ч, либо 8км/ч, причем на всем пути он меняет скорость один раз. Определить отношение меньшего основания трапеции кбоковой стороне.
Решение.Обозначим стороны равнобокой трапеции АВСD через x, y, x и z соответственно. Тогда условие о том, что первый и второй пешеходы пройдут весь путь за одно и то же время, запишется в виде уравнения
Второе уравнение сразу написать нельзя: неизвестно, на каких участках каковы были скорости третьего пешехода. Но поскольку известно, что в процессе движения он менял скорость только один раз, то надлежит рассмотреть 6 случаев: скорость третьего пешехода на одном, двух или трех участках была 7 км/ч и скорость того же пешехода на одном, двух или трех участках была 8 км/ч. Соответственно этому возможны 6 вариантов второго уравнения:
2) 3) 4) 5) 6) Первое из этих уравнений противоречиво. Из второго уравнения находим Что противоречит соотношению (1). Из третьего уравнения имеем что также противоречиво соотношению (1). Из четвертого уравнения получаем z/x=7/3, из пятого – z/x=83/15,из шестого – z/x=98/15. Рассмотрим три последних соотношения. Они не противоречат условию (1). Однако проверим, может ли при таком соотношении сторон существовать трапеция. Для ее существования необходимо выполнение неравенств x+y+x Решения пятого и шестого уравнений не удовлетворяют этим условиям; решение четвертого дает ответ задачи. Поскольку 7/3<16/5, то меньшее основание трапеции – z. Ответ: Отношение меньшего основания трапеции к боковой стороне равно 7:3 Задача 17.Согласно расписанию катер проходит по реке, скорость течения которой 5 км/ч, путь из А в D длиной 15 км за 1 ч. При этом, выходя из пункта А в 12 ч, он прибывает в пункты В и С, отстоящие от А на расстоянии 11 км и 13 км соответственно, в 12 ч 20 мин и в 12 ч 40 мин. Известно, чтo если бы катер двигался из А в D без остановок с постоянной скоростью v (относительно воды), то сумма абсолютных величин отклонений от расписания прибытия в пункты В, С, D не превышала бы уменьшенного на полчаса времени, необходимого катеру для прохождения 5 км со скоростью v в стоячей воде. Какой из пунктов находится выше по течению: А или D? Решение.Рассмотрим два случая в зависимости от расположения пунктов А и D и составим соответственно две системы неравенств: 1) если пункт D находится выше пункта A, то
2) если пункт А находится выше пункта D, то
При решении этих систем (относительно v) получим в первом случае пустое множество, а во втором — промежуток (0; 1]. Для получения ответа к задаче вполне достаточно доказать невозможность, одного из двух перечисленных выше случаев, поскольку тогда может выполняться только другой случай. Однако мы напомним о взгляде на текстовую задачу как на описание реальной картины, т. е. ситуации, которая (по утверждению составителей задачи) хотя бы мысленно, но осуществима. Поэтому из текста задачи следует, что один из случаев непременно имеет место. Что же касается величины v, то в принципе от ее значения могло бы зависеть, какой именно случай выполняется. Но коль скоро первый из них отпадает вообще, то конкретное значение v уже не играет роли и ответ однозначен. Кстати, доказательство несовместности первой системы можно провести и не решая саму систему, так как из нее вытекает следующее:
Ответ: решений нет.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 дано также
дано также  .
. )= v + v2 +v3
)= v + v2 +v3 v
v , либо v2=6y=
, либо v2=6y=  , v3=
, v3=  - чего быть не может, т.к. должно выполняться условие
- чего быть не может, т.к. должно выполняться условие  и включилипервую трубу на слив, а вторую— на наполнение. При этомоказалось, чтобассейн наполнился завремя, в
и включилипервую трубу на слив, а вторую— на наполнение. При этомоказалось, чтобассейн наполнился завремя, в  раза больше, чем то,которое потребуется для наполнения первоначально пустого бассейна одной только второй трубой. В другой раз при наполненном доверху бассейне включили обе трубы на слив, и тогда оказалось, что вся вода вытекла из бассейна за время, составляющее
раза больше, чем то,которое потребуется для наполнения первоначально пустого бассейна одной только второй трубой. В другой раз при наполненном доверху бассейне включили обе трубы на слив, и тогда оказалось, что вся вода вытекла из бассейна за время, составляющее  отвремени,необходимого для наполнения первоначально пустого бассейна одной первой трубой. Во сколько раз пропускная способность второй трубы больше пропускной способностипервой?
отвремени,необходимого для наполнения первоначально пустого бассейна одной первой трубой. Во сколько раз пропускная способность второй трубы больше пропускной способностипервой?

 и
и  Действительно, систему можно записать так:
Действительно, систему можно записать так:
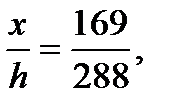
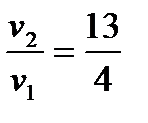
 . В этом случае система уравнений задачи имеет другой вид:
. В этом случае система уравнений задачи имеет другой вид:

 ,
,  Решая эту систему, находим неизвестные:
Решая эту систему, находим неизвестные:  ,
,  , т. е.
, т. е.  1/4, то найденное отношение
1/4, то найденное отношение 
 4, то четвертое уравнение имеет вид
4, то четвертое уравнение имеет вид
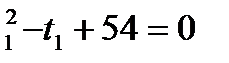


 из которого находим
из которого находим или
или  . (1)
. (1) 1)
1)  ;
; ;
; ;
; ;
; ;
; .
.

 z и x+y+x
z и x+y+x  y, т.е
y, т.е  и
и