
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Cвойства cреднего взвешенногоСодержание книги
Поиск на нашем сайте
На значения интенсивной величины x, найденной по формуле (1) распространяются все свойства, имеющие место для координаты центра системы точечных масс. А именно: 1) x Î (x 1; x 2) (x 1 < x 2); 2) при изменении x 1 и x 2 на одну и ту же величину D, состав x изменяется на такую же величину; 3) при изменении x 1 и x 2 в одинаковое число раз величина x изменяется в то же число раз; 4) при изменении m 1 и m 2 в одинаковое число раз величина x не изменяется; 5) взвешенное среднее нуля и единицы равно весу единицы. Заметим, что формула (1) обобщается на любое число n (n > 2) смешиваемых растворов с концентрациями xi, i =1, 2, …, n:
Пример 1. Смешали 1,5 литра раствора соляной кислоты (HCl) с концентрацией 21,5% и 3,5 л с концентрацией 41,5%. Какова концентрация HCl в получившейся смеси? Решение. Если вычесть из концентраций величину D = 21,5%, то получим растворы с концентрациями 0% и 20% соответственно. «Центр масс» такой смеси находится путем деления отрезка длиной 20 в отношении 3,5:1,5 или же 7:3 (рис.2). Получим 14%.
Рис. 2 Теперь осуществляем обратный сдвиг на D = 21,5% и получаем ответ 35,5% HCl. Ответ: 35,5%. Пример 2. Какой процентный состав получится при смешении m1 = 3,7 л водного раствора уксуса с концентрацией x1 = 34,5% с m3 = 3,7 литрами концентрации x3 = 54,5% и некоторого количества m2 раствора 44,5%–ной концентрации? Решение. Здесь мы имеем три (n = 3) исходные смеси. При этом применить рабочую формулу мы не можем, но не по причине неудобных данных, а ввиду отсутствия информации о количестве m 2. Однако нетрудно видеть, что необходимости в задании этого количества нет. В самом деле, элементарное построение на оси Ox (рис. 6.3) делает наглядным и легко замечаемым симметричное расположение точек состава относительно x 2 = 44,5%. Крайние «массы» (в данном случае объемы) m 1 и m 3 при этом отображаются отрезками одинаковой высоты. Следовательно, какой бы ни была масса m2, даже отрицательной в случае выпаривания такого раствора из смеси, концентрация получившегося раствора будет точно равна x 2.
Рис. 3 Ответ: 44,5%. В несколько усложненном варианте аналогичную задачу можно сформулировать для случая четырех (n = 4) исходных смесей, три из которых образуют симметрическое расположение. При этом также путем параллельного переноса все концентрации можно сделать неудобными для прямых вычислений. Пример 3. Имеются два сплава, в одном из которых содержится 40 %, а в другом – 20 % серебра. Сколько килограмм второго сплава необходимо добавить к 14 кг первого, чтобы получить сплав с 34 %–ной концентрацией серебра? Решение. Откладываем на оси Ox заданные исходные концентрации 20% и 40% и конечную концентрацию 34%. От концентрации 20% откладываем катет, соответствующий 14 килограммам. Проводим прямую через конец этого катета и точку на оси Ox, обозначающую конечную концентрацию 34% до пересечения с перпендикуляром, отложенным от второй исходной концентрации 40%. Полученная длина катета соответствует 6 килограммам (рис. 4).
Рис. 4 Ответ: 6 кг. 1.2. Задачи на движение При решении задач на составление уравнений наибольшую трудность обычно вызывает составление уравнений или системы уравнений, а уж потом их решение. И в том и в другом случае часто оказывается полезным рисунок, иллюстрирующий условие задачи и его анализ с точки зрения геометрии. Вводят координатную плоскость, по одной из осей которой откладывается время, по другой — путь, пройденный телом, выполненная работа и т. д. Тогда любая точка этой плоскости с координатами (t, s) будет соответствовать, например, пути S, пройденному объектом за время t, а само движение изобразится некоторой линией в этой плоскости (траекторией). Пример 4. Из пункта М в пункт N вышел пешеход. Вслед за ним через 2 ч из пункта М выехал велосипедист, а еще через 30 мин — мотоциклист. Пешеход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время оказалось, что все трое преодолели одинаковую часть пути от М к N. На сколько минут раньше пешехода в пункт N прибыл велосипедист, если пешеход прибыл в пункт N на 1 ч позже мотоциклиста? Решение. Рассмотрим плоскость, по оси абсцисс которой отложим время, а по оси ординат — пройденный путь (рис. 5). Пусть отрезок ОЕ соответствует пути, пройденному пешеходом, отрезок AD — велосипедистом, прямая ВС — мотоциклистом. Так как в некоторый момент времени они находятся в одной точке, то все три отрезка имеют на рисунке общую точку.
Рис. 5 В соответствии с условием задачи OA =2, AB =0,5, СЕ=1; требуется найти DE. Так как прямые СЕ и ОВ параллельны, то OB/CE=OA/DE или DE= Ответ:48 мин. Пример 5. Из пункта А в пункт В вышел пешеход. Одновременно с ним из пункта В в пункт А выехал велосипедист, который встретил пешехода через 50 мин после своего выезда из В. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из А в В, если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода (рис. 6.6). Решение. Пусть BD — траектория велосипедиста, АС — траектория пешехода, t — время, затраченное пешеходом на путь от А до В (в ч).
Рис. 6 Имеем:
Это уравнение сводится к квадратному относительно t, решая которое получим t1 = 2/3, t2 = 5. Ответ: t = 5 ч. Пример 6. Из пункта А в пункт В отправились одновременно пешеход и велосипедист. Велосипедист, доехав до пункта В, повернул обратно и встретил пешехода через 20 мин после отправления из А. Доехав до А, он опять повернул и догнал пешехода через 10 мин после встречи. Через какое время пешеход придет в В? Решение. Линия AB'DK (рис.7) соответствует пути, который проехал велосипедист, АК — пути, пройденному пешеходом, АС'= 20, С'К'= 10,
Рис. 7 Следовательно, AN= Ответ: 1 ч. 1.3. Задачи на совместную работу Решению таких задач, как правило, предшествует графическая интерпретация условия. Традиционные подходы не всегда позволяют сделать чертёж наглядным, дающим полноценное представление о действиях, описанных в задаче. Если речь идёт о равномерной работе, то рассматриваемые процессы удобно иллюстрировать графиками функций выполненной работы от времени. Такой подход позволяет давать графикам геометрическую интерпретацию. На смену составлению и решению сложных систем уравнений приходит использование геометрических свойств фигур: подобия треугольников, свойства пропорциональных отрезков и т. д. Пример 7. Баржа была разгружена с помощью двух кранов на протяжении 15ч, причём первый крановщик приступил к работе на 7 ч позже второго. Известно, что первый крановщик, работая отдельно, может разгрузить баржу на 5 ч быстрее второго. За сколько времени может разгрузить баржу каждый крановщик, работая отдельно? Решение. Пусть FC=x ч – неизвестный промежуток времени (рис. 8).
Рис. 8
Тогда AT = 15 + 5 + 5 = 25 ч, OM = 25 – 5 = 20 ч. Ответ: 25 ч, 20 ч. Пример 8. Две машинистки должны отпечатать рукописи с одинаковым числом страниц. Первая приступила к работе на 3 ч раньше второй и отпечатала к определённому моменту времени больше, чем вторая, на Решение. Пусть весь объём работы равен 1, BС = х ч— промежуток времени, недостающий для нахождения времени работы каждой машинистки (рис. 9).
Рис. 9
Ответ: 9ч; 6ч. Пример 9. Двое рабочих могут выполнить некоторую работу за 12 дней. После 8 дней совместной работы второй рабочий перешёл на другой участок. Первый рабочий закончил работу за 5 дней. За сколько дней каждый рабочий, работая отдельно, может выполнить данную работу? Решение. Обозначим через х дней и у дней неизвестные промежутки времени (рис. 6.10).
Так как
Рис. 10 Таким образом, Тогда BD = 13 + 2 = 15 дней, AC = 13 + 47 = 60 дней. Ответ: 15 дней, 60 дней.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

 (2) Также сохраняются все вышеперечисленные свойства с поправкой на число растворов.
(2) Также сохраняются все вышеперечисленные свойства с поправкой на число растворов. , откуда x=4/5 ч или 48 мин.
, откуда x=4/5 ч или 48 мин. СОО" ~
СОО" ~  , или
, или  .
. .
. АВ. Таким образом, на 1/3 пути (АС) пешеход затратил 20 мин, а на весь путь он затратит 1 ч.
АВ. Таким образом, на 1/3 пути (АС) пешеход затратил 20 мин, а на весь путь он затратит 1 ч. ;
;  , откуда x = 5.
, откуда x = 5. страниц рукописи. Проработав после этого момента ещё 5 ч, обе машинистки одновременно закончили каждая свою работу. За сколько времени каждая отпечатала свою рукопись?
страниц рукописи. Проработав после этого момента ещё 5 ч, обе машинистки одновременно закончили каждая свою работу. За сколько времени каждая отпечатала свою рукопись?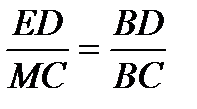 , т.е.
, т.е.  , следовательно,
, следовательно,  .
. , т.е.
, т.е.  , x = 1 ч, значит первая машинистка работала 8+1=9 ч, вторая машинистка – 1 + 5 = 6ч.
, x = 1 ч, значит первая машинистка работала 8+1=9 ч, вторая машинистка – 1 + 5 = 6ч. ;
;  , откуда
, откуда  .
. ;
; , откуда
, откуда  .
. , откуда x = 2 (x > 0), y = 47.
, откуда x = 2 (x > 0), y = 47.


