
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симметричности и четности функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример 1. Решить уравнение
Решение. Внешний вид уравнения подсказывает, что одним из корней является число х1 = х2-х+1= Перепишем уравнение (4) в виде
Тогда видно, что х2=1- х1=1- Покажем, что если х1 (х1¹0, х1¹1) является корнем уравнения (4), то х3=
Таким образом, если х1 (х1¹0, х1¹1) – корень уравнения (4), то корнями уравнения также являются Ответ:
Пример 2. При каких значениях параметра а уравнение x2-2asin(cosx)+2=0 (5) имеет единственное решение? Решение. Так как у = х2 и у = соs х - четные функции, то если существует некоторое х0 — решение исходного уравнения, то (-х0) - также является его решением. Значит, условие х0=-х, откуда х0=0, является необходимым условием существования у исходного уравнения единственного корня. Так как х0=0 является решением, то, подставляя это значение в (5), получим -2asin(1)+2=0 ” a= Осталось убедиться, что при этом значении а исходное уравнение действительно имеет лишь один корень. Запишем (5) в виде x2- Заметим, что (x2+2)sin1≥2sin1, а 2sin(cosx)≤ 2sin1, следовательно, х = 0 является единственным корнем уравнения при данном значении параметра. Ответ: a =
Пример З. При каких значениях параметра а уравнение Решение. Рассмотрим функцию f(х)= f(-x)= то f(x) является четной функцией. Следовательно, если некоторое значение переменной х0 является корнем уравнения (6), то (-х0) - также его корень. Следовательно, если уравнение (6) имеет решения, то имеет четное число корней, кроме случая, когда х=0 является одним из корней, т. е. выполняется равенство│2а│=а2 + 1, откуда а =±1. При каждом из этих значений параметра уравнение (6) действительно имеет по крайней мере корень х =0, поэтому проверять, есть ли еще решения и каковы они, нет необходимости. Ответ: а=±1. Пример 4. При каких значениях параметра а система уравнений
имеет единственное решение, удовлетворяющее ограничению х Î [-6; 0]? Решение. Рассмотрим функцию f(у) = (3-2 Так как (3+ то функция f(у) является четной. Следовательно, если некоторая пара (х0;y0) является решением исходной системы, то (х0;-y0) также является решением. Следовательно, для того чтобы система (7) имела единственное решение, необходимо, чтобы у0 =0. При этом условии система принимает вид
Из второго уравнения имеем х =0 при любом а либо х Î R при а2 -5а+6=0 В первом случае первое уравнение в (8) примет вид 2-За=5, откуда а=-1. Во втором случае а=2 или а=З. Если а = 2, то из первого уравнения находим х = -З, и это значение удовлетворяет условию хÎ[-6; 0]. Если же а=3, то у первого уравнения нет решений. Ответ: а = -1; а= 2. Пример 5. При каких значениях параметра а система уравнений имеет четыре решения?
Решение. Преобразуем второе уравнение исходной системы, выделив полные квадраты (7у)2 + (х-1)2 + 4а = 0. Следовательно, функции в системе симметричны по переменной х относительно значения х =1 и четные по переменной у. Значит, если пара (х0; у0) - решение системы, то также решениями являются (х0; -у0), (2-х0; у0), (2-х0; -у0). Кроме того заметим, что если сделать замену переменных v = 7
которая является симметричной относительно u, v, т. е. вместе с любой парой (u; v), где u >0, v >0, решением является и пара (v; u). Следовательно, исходная система если имеет, то имеет не менее восьми решений, кроме трех случаев: 1) u= v, 2) u = 0, З) v =0. А тогда, если u= v, то а =- Ответ: а =- Пример 6. При каких значениях параметра а система уравнений Решение. Выделим в каждом из уравнений данной системы полные квадраты (11) •
Теперь видно, что система (11) «симметрична» относительно х-1 и у+2 т. е. если сделать замену переменных u = х-1, v = у+2 и некоторая пара (u0;v0) является решением, то (v0; u0) - также решение. Следовательно, необходимым условием существования единственного решения у системы (11) является равенство u0=v0, откуда х = у + 3. Подставляя это выражение во второе уравнение (11), получаем 2ау2+ 8ау-у-3+10а+1=0 • 2ау2+ у(8а-1)+10а-2=0. Это уравнение имеет единственное решение либо если оно является линейным (т. е. а =0), либо если оно квадратное и D=(8a-1)2-4*2a*(10a-2)=1- -16a2=0, т. е. при условии а = Ответ: - Пример 7. При каких значениях параметра а система Решение. Первое и третье уравнения исходной системы являются симметричными относительно переменных х н у. Однако из внешнего вида второго уравнения в (12) такой вывод сделать нельзя. Выделим в нем полный квадрат относительно х х2-2х+(у-1)2+z=a • (x-1)2+(y-1)2+z2=a+1. Теперь видно, что если некоторая тройка (х0; у0; z0) является решением системы (12), то и тройка (у0; х0; z0) - также решение системы. Следовательно, решение будет единственным только тогда, если выполнено условие х0 = у0. Тогда исходная система примет вид
Из первого уравнения следует, что siп2х=0, но это уравнение имеет бесконечно много решений. Однако ОДЗ переменной х системы определяется неравенством 1-х2>0, т. е. х Î (-1; 1), значит, в ОДЗ переменной лежит лишь решение х =0. Итак, имеем условие х = у =0 и, подставляя в (13), получаем систему Относительно переменной z:
Если некоторое z0 – решение системы (14), то (-z0) – также решение. Следовательно, условие z=0 – еще одно необходимое условие существования единственного решения у системы (12), откуда получается а=1. При таком значении параметра исходная система приобретает вид
Преобразуем второе уравнение к виду х2 + у2 +z2-2х-2y=0 и подставим выражение х + у =-sin2z из третьего уравнения. Тогда имеем уравнение х2 + у2 +z2+2sin2z=0 • x=y=z=0. То есть тройка (0; 0; 0) действительно является единственным решением системы (12) при а = 1. Ответ: а =1.
Пример 8. При каких значениях параметра а системы уравнений
Решение. Система (15) является линейной. Она не имеет решений, если выполнены соотношения Вычитая из второго уравнения первое, имеем х2-7х+у4+у2+21=0 • • Это уравнение и, следовательно, (16) не имеют решений. Итак, при а=-2 обе системы не имеют решений, а значит, равносильны. Пусть теперь а а¹-2. Тогда линейная система (15) имеет единственное решение при любом значении параметра. Значит, необходимым условием равносильности систем (15) и (16) является то, что система (16) имеет единственное решение. Но если пара (х0; у0) является решением (16), то пара (х0;-у0) тоже будет ее решением. Поэтому необходимым условием существования единственного решения является у0 = -у откуда у0 =0. Подставляя у=0 в (16), получаем систему для нахождения х и а:
Из первого уравнения находим х1 = 1 или х2 =3, тогда, подставляя эти значения во второе уравнение системы (17), находим а = 1 или а =3, и а =±1. Осталось проверить каждое из найденных значений. При а = 1 значения х = 1, у = 0 являются решением (15), но у (16) есть еще одно решение - х = 3, у = 0, и эти значения не являются решением (15). При а =3 значения х = 1, у = 0 не являются решением (15). При а =-1 значения х = 3, у =0 являются решением (15), и т. к. второе уравнение в (16) примет вид у2=-2(х-3) то (16) тоже имеет единственное решение - х = 3, у = 0. Ответ: а=-2; а =-1. Литература 1. Шарыгин И.Ф. Факультативный курс по математике. Решение задач./И.Ф. Шарыгин., 1991. 2. Пирютко О.Н.Формирование обобщенных приемов познавательной деятельности. /О.Н. Пирютко Народная Асвета» №9, 2008, стр. 32- 40. 3. Азаров А.И., Булатов В.И. и др. Математика. Пособие для подготовки к экзамену и централизованному тестированию. – Мн., 2004.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 . (4)
. (4) . Воспользуемся тем, что
. Воспользуемся тем, что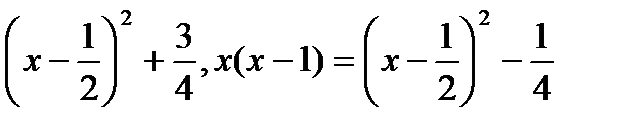 .
. .
. .
.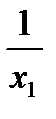 также есть корень этого уравнения. Это действительно так, потому что
также есть корень этого уравнения. Это действительно так, потому что .
. , 1-х1,
, 1-х1,  , 1-
, 1-  ,
,  , т. е. уравнение (4) имеет корни х1=
, т. е. уравнение (4) имеет корни х1=  , х4=
, х4=  , х5=1-
, х5=1-  . Так как исходное уравнение есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Следовательно, найдены все корни уравнения (4).
. Так как исходное уравнение есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Следовательно, найдены все корни уравнения (4). .
. .
. sin(cosx)+2=0 • (x2+2) sin1=2sin(cosx).
sin(cosx)+2=0 • (x2+2) sin1=2sin(cosx). .
. (6) имеет нечетное число корней?
(6) имеет нечетное число корней? . Так как
. Так как f(x),
f(x), (7)
(7) )y+(3+
)y+(3+  )y, стоящую в левой части первого уравнения системы (7).
)y, стоящую в левой части первого уравнения системы (7). ,
, (8)
(8)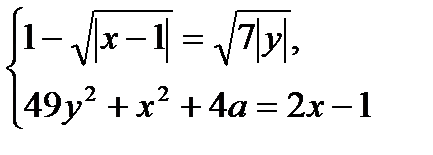 (9)
(9) и u =
и u =  , то получим систему
, то получим систему (10)
(10) , в случае u = 0 имеем а =-
, в случае u = 0 имеем а =-  , а если v =0, то а = -
, а если v =0, то а = -  . Осталось проверить каждое из найденных значений а и удостовериться, что система (10) действительно имеет два решения, а значит, система (9) имеет четыре решения.
. Осталось проверить каждое из найденных значений а и удостовериться, что система (10) действительно имеет два решения, а значит, система (9) имеет четыре решения. (11) имеет единственное решение?
(11) имеет единственное решение?


 . Подставляя найденные значения параметра а в систему (11), убеждаемся, что при каждом из них она действительно имеет единственное решение.
. Подставляя найденные значения параметра а в систему (11), убеждаемся, что при каждом из них она действительно имеет единственное решение. ; 0;
; 0;  .
. (12) имеет единственное решение?
(12) имеет единственное решение? (13)
(13)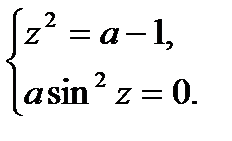 (14)
(14)
 (15) и
(15) и  (16) равносильны?
(16) равносильны? , т. е. при а=-2. Подставим это значение в (16). Имеем
, т. е. при а=-2. Подставим это значение в (16). Имеем 
 •
•
 (17)
(17)


