
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целые числа. Делимость целых чисел. Признаки делимостиСодержание книги
Поиск на нашем сайте План 1. Множество целых чисел. Свойства и операции. 2. Теоремы о делимости. 3. Деление с остатком.
Множество целых чисел – это натуральные, им противоположные и ноль. Свойства целых чисел (Z). 1. Множество целых чисел замкнуто относительно операций сложения, вычитания, умножения: это значит, что результат указанных операций над целыми числами так же принадлежит множеству целых чисел. 2. Дискретно: для любого целого числа можно указать следующее за ним, между двумя соседними целыми числами нет целого числа. 3. Упорядоченно: для любых целых чисел можно установить отношение порядка (a>b, a<b, a=b). Свойства операций с целыми числами
1. a + b = b + a (коммутативный закон сложения) 2. (a + b) +с = a + (b +c) (ассоциативный закон сложения) 3. a - a = 0 4. a + 0 = a 5. a b = b a (коммутативный закон умножения) 6. (a b) с = a (b c) (ассоциативный закон умножения) 7. (a + b) с = a с + b c (дистрибутивный закон умножения относительно сложения) 8. 1·a = a Определение Если a: b = с Теорема о единственности разложения натурального числа на простые множители.(Основная теорема арифметики). Существует и при том единственное разложение всякого натурального числа (кроме 1) на простые множители. Представление натурального числа в виде n = p1, p2, p3, … pn – простые числа, называется каноническим разложением натурального числа на простые множители. Например, 36 = 3222, 195=31·51·131. Задача Сколько всего делителей имеет натуральное число, если его каноническое разложение имеет вид n = Пример 60 = 223151
Его делители 1, 2, 3,4, 5, 6, 10, 12,15,20, 30, 60 – всего 12. Как подсчитать число делителей, не перечисляя их? Число вариантов(способов) вхождения в делители данного числа делителя с основанием 2 всего три: 1- совсем нет такого делителя, 2- 21 3- 22 Число вариантов(способов) вхождения делителя с основанием 3 всего 2 1- совсем нет такого делителя, 2- 31. Число вариантов(способов) вхождения делителя с основанием 5 всего 2 1- совсем нет такого делителя, 2- 51. Каждый из первых трех вариантов можно объединить с каждым из двух вторых, всего получится 3·2=6. Каждый из этих 6 вариантов можно объединить с любым из двух способов вхождения числа 5 в делители данного числа, всего получится 3·2·2= 12. Аналогичное этому доказательство в общем виде приводит к результату: Количество всевозможных делителей числа n = (α1+1)(α2+1) (α3+1)…(αn+1).
Теорема о бесконечности ряда простых чисел Не существует наибольшего простого числа. Доказательство Предположим, что p – наибольшее простое число. Рассмотрим число 2·3·5·…· p + 1- это число либо само простое, большее p, либо делится на простое число, не содержащееся среди чисел 2, 3, 5, …,p, а следовательно, большее p. Получили противоречие, доказывающее теорему.
Связь между НОД и НОК. О бозначим НОД(а; b) = d, НОК(a;b) = m.
Так как НОД(а; b) = d, то a = a1d, b = b1d, (a1;b1)=1.
Так как НОK(а; b) = m, то m = a1·d· b1, тогда а·b = a1·d· b1·d = m d. Таким образом, НОД(а;b) ·НОК(a;b) = ab.
Теоремы о делимости 1.Если a: m, b: m, то (a +b): m, (a -b): m.
2. Если a: m, b: n, то a b: mn. 3. Если a: m, an: mn. 4. Если сумма нескольких слагаемых делится на m и известно, что все слагаемые, кроме одного, делятся на m, то и оставшееся слагаемое делится на m. 5. Если хотя бы один из множителей произведения делится на m, то и произведение делится на m.
Пример Докажите, что произведение n(n+1)(n+2) делится на 6 при любом натуральном n. Доказательство Если n – нечетное, то n +1 – четное, следовательно, произведение делится на 2. Если n – не кратно 3 (значит при делении на 3 дает остаток 1 или 2), то n +2 или n + 1 кратно 3. Таким образом, произведение n(n+1)(n+2) делится на 2 и на 3, а так как эти числа взаимно простые, то оно делится на 6.
Признаки делимости 1.Для того, чтобы натуральное число делилось на 3(9) необходимо и достаточно, чтобы сумма цифр этого числа делилась на 3(9). 2. Для того, чтобы натуральное число делилось на 11 необходимо и достаточно, чтобы разность между суммой цифр этого числа стоящих на четных местах и суммой цифр этого числа стоящих на нечетных местах делилась на 11. 3. Для того, чтобы натуральное число делилось на 4 необходимо и достаточно, чтобы число, образованное двумя последними цифрами этого числа делилось на 4. Докажем 2. p= an10n + an-110n-1 + an-210n-2 +…..+ a1101+ a0 = an (11-1)n + an-1 (11-1)n-1 + an-2 (11-1)n-2 +…..+ a1 (11-1)1+ a0 = 11K + (an (-1)n + an-1 (-1)n-1 + an-2 (-1)n-2 +…..+ a1 (-1)1+ a0). Если число p делится на 11, то второе слагаемое (an (-1)n + an-1 (-1)n-1 + an-2 (-1)n-2 +…..+ a1 (-1)1+ a0) суммы делится на 11 и обратно: для того, чтобы число p делилось на 11, достаточно, чтобы это слагаемое делилось на 11. Второе слагаемое суммы в зависимости от четности или нечетности n равняется (an - an-1 + an-2 -…..-a1 + a0) или (-an+an-1 - an-2 +…..-a1 + a0), т.е. представляет собой разность между суммой цифр этого числа, стоящих на четных местах и суммой цифр этого числа, стоящих на нечетных местах. 4. Если число делится на 1001, то оно делится на 7, 11, 13.
Деление с остатком
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

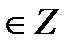 , то a называется кратным b, а b – делителем числа a.
, то a называется кратным b, а b – делителем числа a. , где
, где


