
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графические приёмы решения задач с параметрами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В зависимости от того, какая роль в задаче отводится параметру (неравноправная или равноправная с переменной), можно соответственно выделить два графических приёма: первый – построение графического образа на координатной плоскости Строят образ, результат «считывают» с картинки. Конечно, полученный таким образом результат, не подкреплённый аналитическим решением, нельзя считать «строгим» решением. В случае, когда результат, «считанный с картинки» вызывает сомнение, следует подкрепить решение аналитически. Рассмотрим несколько примеров с использованием плоскости
Пример 3. Для каждого значения параметра а определить число решений уравнения Решение: В системе координат
y
y=a
4 y=|x2-2x-3|
- 1 0 2 3 x
Используя полученный рисунок, получаем результат: 1) если 2) если 3) если 4) если Функционально-графический подход. Можно рассматривать параметр как равноправную переменную, а не как фиксированное, но неизвестное число. Такой подход позволяет в максимальной степени геометризировать алгебраические задачи и свести весь поиск их решения к умению строить график уравнения Пример 4. Решить уравнение Решение: В системе координат
a=x+5 A a=-x-5 x=a-5 5 x=5-a
-5 -5 5 x a=x-5, x=a=5 a=-x-5 x=-5=-a
1) если 2) если 3) если 4) если 5) если
Решение неравенств с параметрами.
При решении неравенств с параметрами используются те же подходы, что и при решении уравнений. Рассмотрим несколько примеров.
Пример 5. При каких значениях параметра а неравенство
Решение: Строим график соответствующего уравнения в системе координат
a
-3
x
-3 -3,25
Хотя бы одно отрицательное решение неравенство имеет если
Пример 6. Решить неравенство
Решение: Строим график неравенства в системе
a a=(5+x)/2 x=2a-5
-1 1 x
a=(x-5)/2 x=2a+5
Получаем: 1) если 2) если 3) если 4) если Литература 1. Шарыгин И.Ф. Факультативный курс по математике. Решение задач./И.Ф. Шарыгин., 1991. 2. Пирютко О.Н.Формирование обобщенных приемов познавательной деятельности. /О.Н. Пирютко Народная Асвета» №9, 2008, стр. 32- 40. 3. Азаров А.И., Булатов В.И. и др. Математика. Пособие для подготовки к экзамену и централизованному тестированию. – Мн., 2004.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

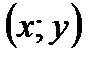 , второй – на плоскости
, второй – на плоскости 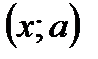 .
. .
. .
.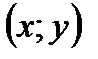 строим графики
строим графики  и
и 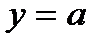 , где
, где  .
.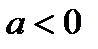 , уравнение корней не имеет;
, уравнение корней не имеет;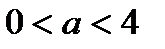 , уравнение имеет четыре корня;
, уравнение имеет четыре корня;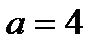 , то уравнение имеет три корня;
, то уравнение имеет три корня;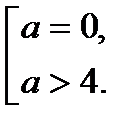 , то уравнение имеет два корня.
, то уравнение имеет два корня. с двумя переменными и на его основе исследовать решения этого уравнения и соответствующих ему неравенств.
с двумя переменными и на его основе исследовать решения этого уравнения и соответствующих ему неравенств.
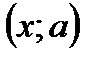 строим график уравнения и сразу считываем результат:
строим график уравнения и сразу считываем результат: , то уравнение корней не имеет;
, то уравнение корней не имеет; , то
, то 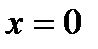 ;
;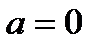 , то
, то 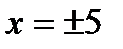 ;
;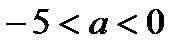 , то
, то 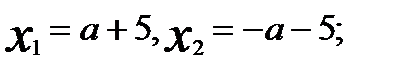
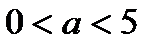 , то
, то  .
. имеет хотя бы одно отрицательное решение?
имеет хотя бы одно отрицательное решение?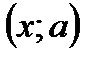 .
. .
.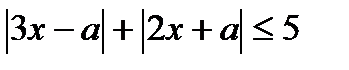 .
.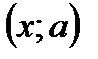 .
.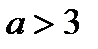 , то решений нет;
, то решений нет;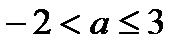 , то
, то 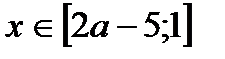 ;
; , то
, то 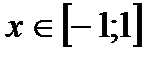 ;
; , то
, то 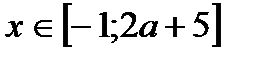 .
.


