
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы, необходимые для решения уравнений, основанных на симметричности и четности функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим уравнение с параметром f (х, а) =0. (1) В случае, когда функция f является четной относительно переменной х и если известен корень х0 уравнения (1), то –х0 также является корнем этого уравнения. Следовательно, если стоит задача: «При каких значениях параметра а уравнение (1) имеет единственный корень?», либо «При каких значениях параметра а у уравнения (1) есть нечетное число корней?», то искомыми значениями могут быть только те значения параметра а, при которых значение х0 =- х0 =0 является корнем уравнения (1). Это условие является необходимым, но не достаточным для ответа на подобный вопрос. Однако в большинстве задач существует лишь несколько конкретных значений параметров, при которых нуль является корнем. В дальнейшем решении останется лишь проверить каждое из найденных значений параметров. Аналогичные рассуждения позволяют получить необходимые условия и в некоторых системах с параметрами. Рассмотрим уравнение f (х)=0 (2) В случае, когда функция f (х) является симметричной относительно Если в (2) график у=f (х) симметричен относительно прямой х=а (рис.) и известен корень х0 уравнения (2), то значение х=х
Система задач на применение функционального подхода к решению уравнений и неравенств Решение уравнений, основанные На ограниченности функций Пример 1. Решить уравнение
Решение. Оценим правую часть уравнения
Но значение выражения в левой части исходного уравнения:
Ответ: Æ. Пример 2. Имеет ли корни уравнение Решение. Запишем данное уравнение в виде Ответ: не имеет.
Пример 3. Найти все значения параметра а при которых уравнение 3х4 – 4х3 +12х2 +а =0 имеет корни?
Решение. Рассмотрим функцию f(x) = 3х4 – 4х3 +12х2. Выделим полный квадрат f(x) = х2 Следовательно, функция f(x) принимает все значения из множества Ответ: а Пример 4. Решить уравнение sin(px) = x2 + x +1. Решение. Оценим правую часть уравнения x2 + x +1 = х Î [-1; 0]. Таким образом, мы можем утверждать, что на интервалах х Î (- Ответ: Æ.
Как видно из решения примера 4, в некоторых задачах для получения результата нужно рассматриваемую область разбивать на подмножества и на каждом подмножестве заданные функции оценивать разными способами. Определить эти подмножества и соответствующие оценки часто помогают графики функций, входящих в задачу.
Пример 5. Решить уравнение
Решение. Оценим левую и правую части уравнения. Так как
решением которой является х = Ответ: Пример 6. Решить уравнение cos5x – sin10x = 1.
Решение. Преобразуем исходное уравнение следующим образом: cos5x=sin10x+1. Выражение, находящееся в левой части полученного уравнения, принимает значения от -1 до 1 включительно, а выражение в правой части - 1+0 ≤ 1+ sin10x ≤ 1+1, т. е. больше или равно 1. Следовательно, исходное уравнение равносильно системе уравнений
Ответ: 2pn, nÎZ. Пример 7. Решить уравнение cos5x = 1- sin10x.
Решение. Воспользоваться методом, использованным в предыдущем примере нельзя, т. к. 1-1 ≤ 1- sin10x ≤ 1-0. Преобразуем исходное уравнение следующим образом: cos5x = sin2x + cos2x- sin10x
Левая часть последнего уравнения всегда меньше или равна 0, а правая - больше или равна 0, следовательно, равенство возможно только, если
Решая эти системы, получим окончательный ответ. Ответ: Пример 8. Решить уравнение
Решение. ОДЗ переменной, входящей в это уравнение, определяется условиями х3+2 Ответ: Æ. Пример 9. Решить уравнение
Решение. Найдем ОДЗ переменной, входящей в исходное уравнение:
Найдем область значений левой и правой частей уравнения:
Так как множества значений левой и правой частей уравнения не пересекаются, то уравнение решений не имеет. Ответ: Æ.
Пример 10. Решить уравнение 5х2 +5у2 +8ху+2х-2у+2=0. (2) Решение. Выделим полные квадраты в левой части уравнения (2) х2 +2х+1+у2 -2у+1+4(х2+у2 +2ху) = 0 Так как каждое из слагаемых в полученном уравнении неотрицательно, то исходное уравнение имеет решение только, если
Ответ: {-1; 1}.
Пример 11. Решить уравнение
Решение. Выделим в уравнении полный квадрат относительно
Сумма двух неотрицательных величин равна нулю, только если каждая величина равна нулю. Следовательно, Ответ: {11; 5}.
Решения уравнений, основанные на монотонности функций
Пример 1. Решить уравнение 2х = -2х+4.
Решение. В подобных уравнениях, где слева и справа от знака равенства стоят функции совершенно разных «классов» (в данном случае линейная и показательная), обычно одним из методов решения является функциональный метод. Значение х=1 является корнем данного уравнения, т. к. 21 =2= -2*1+4. Слева в уравнении стоит возрастающая на R функция (как показательная функция с основанием, большим единицы), а справа — убывающая линейная функция, т. к. коэффициент при переменной отрицательный. Следовательно (по теореме 1), больше корней исходное уравнение не имеет. Ответ: 1. Пример 2. Решить уравнение 4х+3х =5х.
Решение. Легко убедиться, что х =2 — корень исходного уравнения, т. к. числа 3, 4, 5 образуют пифагорову тройку. Однако утверждать, что он единственный, мы не можем, так в левой и правой частях исходного уравнения находятся возрастающие функции. Преобразуем исходное уравнение к следующему равносильному уравнению
Функция f(x) = Ответ: 2.
Пример З. Решить уравнение Решение. Решить это уравнение возведением в степень или заменой переменных не представляется возможным (по крайней мере, на первый взгляд). Однако можно обойтись и без каких-либо преобразований. Заметим, что х=1 — корень данного уравнения. Левая часть уравнения представляет собой возрастающую на R функцию, поскольку является суммой двух возрастающих функций. Поэтому, используя теорему 2, утверждаем, что х=1-единственный корень. Ответ: 1. Отметим, что в примере З нет необходимости доказывать возрастание функций и т. к. это элементарные функции, рассматриваемые в курсе школьной математики.
Пример 4. Решить уравнение
Решение. Функция f(x) = Ответ: -1. Пример 5. Решить уравнение
Решение. Обозначим t=log3 х, тогда х =3t,
Ответ: 9. Пример 6. Привести пример убывающей функции f(x), для которой уравнение f(f(х)) = х не равносильно уравнению f(х)=х. Решение. Рассмотрим функцию f(x) = Теперь рассмотрим уравнение f(f(х)) = х, т. е.
Последнее уравнение имеет три корня: х = Ответ: f(x) = 16-х. Пример 7. Решить уравнение Решение. Перепишем уравнение в виде
Введем в рассмотрение функцию f(t)= уравнение можно переписать в следующем виде: f(3x+1)=f(-x). (1) Если мы докажем, что f(t) - монотонная функция на R, то по теореме 4 уравнение (1) равносильно уравнению 3х+1= -х Вычислим f´(t)= Так как f´(t)>0 при любом tÎR, следовательно, f(t) возрастает на всей числовой оси. Итак, доказав, что f(t) монотонна, мы доказали, что х =- Ответ: - Пример 8. Решить уравнение Решение. Воспользуемся идеей, предложенной в примере 2. Разделим левую и правую части на 2х ≠ 0. Тогда уравнение примет вид
Так как Ответ: 2. Пример 9. Решить уравнение log22x+(x-1)log2x=6-2x. Решение. Обозначим log2x=у, тогда исходное уравнение преобразуется к виду y2+(x-1)y+(2x-6)=0. Последнее уравнение является квадратным относительно у. Найдем его дискриминант: D =(x-1)2-4(2x-6) = x2-2x+1-8x+24 = x2-10x+25=(x-5)2 И корни у1= Возвращаясь к переменной х, будем иметь совокупность двух уравнений
Первое легко решается и дает корень х =2-2 = Второе уравнение решим следующим образом: очевидно, что х=2 - корень этого уравнения (log22=3-2). Этот корень единственный (теорема 1), т. к. функция, стоящая в левой части уравнения, возрастает на ОД3 переменной, а функция в правой части - убывает. Ответ: Пример 10. Решить уравнение (x+1)4х +(х-1)2x+1 =8. Решение. В левой части данного уравнения находятся достаточно сложные функции, которые не являются ни возрастающими, ни убывающими на всей числовой оси. Следовательно, не удастся использовать сразу теоремы, приведенные выше. Преобразуем уравнение. Аналогично предыдущей задаче введем замену у=2х тогда имеем квадратное относительно у уравнение (х + 1)у2 + 2(х - 1)у - 8 = 0. Его дискриминант равен
Тогда y1=
т. е. исходное уравнение можно записать в виде
Первое уравнение совокупности решений не имеет, а второе решаем, используя теорему 1. При х<-1 это уравнение не имеет решений, т. к. 2x >0, а Ответ: 1. Пример 11. Решить уравнение Решение. ОДЗ переменной в этом уравнении является множество [1; 3]. На этом множестве функция у = Ответ: 2. Пример 12. Решить уравнение (х3 +2х+2)3 +2(х3 +2х+2)+2=х. Решение. Введем в рассмотрение функцию f(х)=х3+2х+2 и заметим, что уравнение (3) имеет вид f(f(х))=х. Так как f'(х)=3x2+2>0 при всех х, то функция f(х) является возрастающей на всей числовой оси. Следовательно, по теореме 5, уравнение (3) равносильно уравнению f(х) =х, т. е. уравнению х3 +2х+2=x Ответ: -1. Пример 13. Решить уравнение Решение. Рассмотрим функцию f(х)= Пример 14. Сколько корней на отрезке [-p; 0] в зависимости от значений параметра а имеет уравнение х2 +а= соsх? Решение. Рассмотрим функцию f(х)= соsх - х2. Исходное уравнение примет вид f(х)=а. Исследуем f(х): f‘(х)=sinx-2x≥0 при хÎ[- p; 0], следовательно, f(х) возрастает на множестве [-p; 0] и, кроме того, является непрерывной. Используя теорему 3, можно утверждать, что она принимает все значения между f(-p)=соs(-p) - (-p)2 =-1-p2 и f(0)= соs 0-02=1. Итак, если а принимает значения в пределах [-1-p2; 1], то исходное уравнение имеет корень, причем единственный. Если же а Î(- Ответ: один корень при аÎ [-1-p2; 1]; нет решений при аÎ(- Пример 15. Пусть f(х)=х2-2. Доказать, что уравнение f(f(f(х)))=х имеет восемь корней. Решение. Рассмотрим отрезок хÎ[-2;2] и отметим, что f(-2)=2; f(2)=2; f(0)=-2. Нулями функции f(х)=х2 -2 являются точки x= Рассмотрим функцию g(х)=f(f(f(x)))-x на отрезках На концах каждого из этих отрезков функция g(х) принимает значения разных знаков, следовательно, уравнение f(f(f(x)))=x имеет корень на каждом этом отрезке. Например, рассмотрим отрезок
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

 (т. е. после замены у =
(т. е. после замены у =  функция не меняется), то при наличии у уравнения корня х0¹0 корнем является также
функция не меняется), то при наличии у уравнения корня х0¹0 корнем является также  .
. , расположенное симметрично относительно а, также является корнем уравнения (т. е. х0-а=а-х1, откуда х1=2а-х0). Это значит, что в уравнении (2) можно осуществить замену переменной у=х-а и функция f(у) будет являться четной.
, расположенное симметрично относительно а, также является корнем уравнения (т. е. х0-а=а-х1, откуда х1=2а-х0). Это значит, что в уравнении (2) можно осуществить замену переменной у=х-а и функция f(у) будет являться четной.
 =
=  .
. . Таким образом, т. к. левая часть строго меньше
. Таким образом, т. к. левая часть строго меньше  , а правая – больше или равна
, а правая – больше или равна 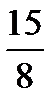 , исходное уравнение решений не имеет.
, исходное уравнение решений не имеет. ?
? . Рассмотрим функцию f(x) =
. Рассмотрим функцию f(x) =  . Так как f(x) =
. Так как f(x) =  , а правая часть преобразованного уравнения отрицательна, то исходное уравнение корней не имеет.
, а правая часть преобразованного уравнения отрицательна, то исходное уравнение корней не имеет.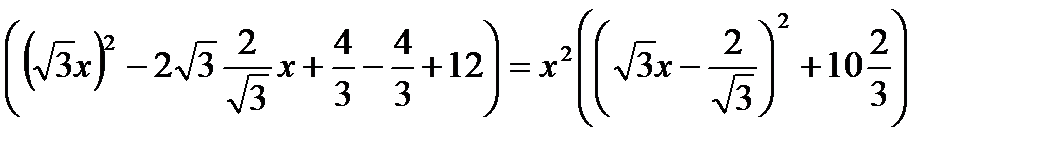 .
. . Значит, уравнение 3х4 – 4х3 +12х2 = -а имеет корни лишь при а
. Значит, уравнение 3х4 – 4х3 +12х2 = -а имеет корни лишь при а  .
. .
. , но такая оценка не позволяет сделать заключение о том, что уравнение не имеет решений. Так как sin(px) ≤ 1, то решим неравенство x2 + x +1 ≤ 1, откуда
, но такая оценка не позволяет сделать заключение о том, что уравнение не имеет решений. Так как sin(px) ≤ 1, то решим неравенство x2 + x +1 ≤ 1, откуда ; -1) Ç (0; +
; -1) Ç (0; +  ) уравнение решений не имеет, так как x2 + x +1 > 1, а sin(px) ≤ 0, а x2 + x +1>0, следовательно, на отрезке х Î [-1; 0] уравнение решений не имеет.
) уравнение решений не имеет, так как x2 + x +1 > 1, а sin(px) ≤ 0, а x2 + x +1>0, следовательно, на отрезке х Î [-1; 0] уравнение решений не имеет. . (1)
. (1) , то
, то  и
и  , т. к. sin(2px) ≤ 5+4 = 9. Таким образом, равенство в (1) возможно только, если выполняется система
, т. к. sin(2px) ≤ 5+4 = 9. Таким образом, равенство в (1) возможно только, если выполняется система
 .
.
 cos5x - cos2x = sin2x- sin10x
cos5x - cos2x = sin2x- sin10x 
 .
. .
. 0 и х3-2
0 и х3-2  0 т. е. состоит из всех х, принадлежащих промежутку
0 т. е. состоит из всех х, принадлежащих промежутку  . Для всех таких х выражение
. Для всех таких х выражение  , а выражение
, а выражение  . Таким образом, исходное уравнение решений не имеет.
. Таким образом, исходное уравнение решений не имеет. .
. .
. ;
; <
<  <
<  .
.
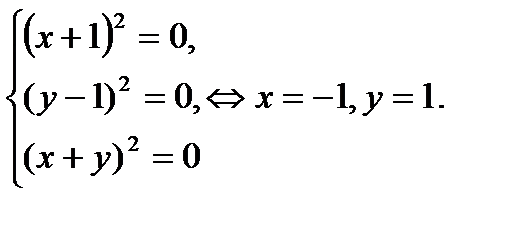
 .
. и
и  Имеем:
Имеем:
 и
и  , откуда х=11; у=5
, откуда х=11; у=5 .
. - убывает на R (т. к. основание показательной функции
- убывает на R (т. к. основание показательной функции 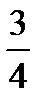 <1), а g(х) =
<1), а g(х) =  — возрастает на R. Следовательно, по теореме 1, исходное уравнение имеет единственный корень х=2.
— возрастает на R. Следовательно, по теореме 1, исходное уравнение имеет единственный корень х=2. .
. .
. — возрастающая на всей числовой прямой. Функция g(х)=
— возрастающая на всей числовой прямой. Функция g(х)= 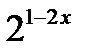 — убывающая при всех хÎR. Значит, -g(х)=-
— убывающая при всех хÎR. Значит, -g(х)=-  (равносильное исходному) имеет не более одного корня (теорема 2). Этот корень находим подбором: х=-1.
(равносильное исходному) имеет не более одного корня (теорема 2). Этот корень находим подбором: х=-1. .
. и исходное уравнение примет вид
и исходное уравнение примет вид  , откуда 1+(
, откуда 1+( )t=2t. Это уравнение имеет очевидный корень t =2. Разделив обе части уравнения почленно на (
)t=2t. Это уравнение имеет очевидный корень t =2. Разделив обе части уравнения почленно на ( . Функция у =
. Функция у =  убывает на R, а функция у=
убывает на R, а функция у=  возрастает на R (т. к.
возрастает на R (т. к.  >1). Значит, по теореме 1, t=2 - единственный корень. Из уравнения log3x=2 находим х=9 - единственный корень исходного уравнения.
>1). Значит, по теореме 1, t=2 - единственный корень. Из уравнения log3x=2 находим х=9 - единственный корень исходного уравнения. . Уравнение f(х)=х, т. е.
. Уравнение f(х)=х, т. е.  =х имеет ровно одно решение (обозначим его x0) т. к. f(х) убывает на всей числовой оси, а, g(х)= х - возрастает.
=х имеет ровно одно решение (обозначим его x0) т. к. f(х) убывает на всей числовой оси, а, g(х)= х - возрастает.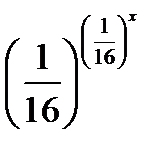 = х. Решим это уравнение на множестве положительных чисел. Прологарифмируем обе части по основанию
= х. Решим это уравнение на множестве положительных чисел. Прологарифмируем обе части по основанию  и получим равносильное уравнение
и получим равносильное уравнение =
= 
 .
. ; х =
; х =  ; х =х0. То есть х =
; х =х0. То есть х =  и х =
и х =  не являются корнями уравнения f(x) = х.
не являются корнями уравнения f(x) = х. .
.
 . Тогда исходное
. Тогда исходное 4x=-1
4x=-1  x=-
x=-  .
. .
.
 . (2)
. (2) <1, то функция в левой части уравнения (2) -убывающая при хÎR (показательная функция с основанием, меньшим 1). Так как
<1, то функция в левой части уравнения (2) -убывающая при хÎR (показательная функция с основанием, меньшим 1). Так как  <1‚ то
<1‚ то  - убывающая функция, а, следовательно, функция
- убывающая функция, а, следовательно, функция  в правой части (2) является возрастающей на всей числовой прямой. По теореме 1 уравнение (2) имеет не более одного корня. Этот корень легко подбирается, и он равен 2.
в правой части (2) является возрастающей на всей числовой прямой. По теореме 1 уравнение (2) имеет не более одного корня. Этот корень легко подбирается, и он равен 2. ; y2=
; y2= 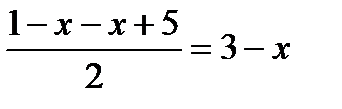 .
.
 .
. =(х-1)2 +8(х+1) =х2-2х+1+8х+8=х2 +6х+9=(х+3)2.
=(х-1)2 +8(х+1) =х2-2х+1+8х+8=х2 +6х+9=(х+3)2. ; y2=
; y2=  ,
,

 <0. Поскольку 2x – возрастающая функция, а
<0. Поскольку 2x – возрастающая функция, а  - убывающая на множестве х > -1, то х = 1 (этот корень легко найти подбором) является единственным корнем второго уравнения совокупности на множестве х >-1, а, значит, и исходного уравнения.
- убывающая на множестве х > -1, то х = 1 (этот корень легко найти подбором) является единственным корнем второго уравнения совокупности на множестве х >-1, а, значит, и исходного уравнения. .
. возрастает, а функция у=
возрастает, а функция у=  убывает, значит, по теореме 1, исходное уравнение имеет единственный корень (если он есть). Подбором находим его, х = 2.
убывает, значит, по теореме 1, исходное уравнение имеет единственный корень (если он есть). Подбором находим его, х = 2. .
. . Тогда уравнение (3) можно представить в виде f(f(х))=х. Так как функция f(х) является возрастающей на своей области определения, то, по теореме 5, уравнение (3) равносильно уравнению
. Тогда уравнение (3) можно представить в виде f(f(х))=х. Так как функция f(х) является возрастающей на своей области определения, то, по теореме 5, уравнение (3) равносильно уравнению  . Ответ:
. Ответ:  .
. ; 1-p2)Ç(1; +
; 1-p2)Ç(1; +  ), то решений нет.
), то решений нет. , т. е. f(-
, т. е. f(-  )=0, f(
)=0, f( )=0. Далее f(f(-2))=2, f(f(2))=2, f(f(0))=2 и f(f(-
)=0. Далее f(f(-2))=2, f(f(2))=2, f(f(0))=2 и f(f(-  , т.е. f(f(-
, т.е. f(f(-  ))=0, f(f(-
))=0, f(f(- 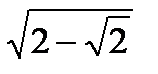 ))=0, f(f(
))=0, f(f( ))=0, f(f(
))=0, f(f( ))=0.
))=0. ,
, 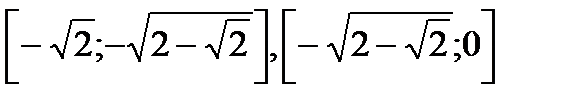 ,
,  ,
,  .
. : g(-2)=f(f(f(-2)))+2=4>0, g(
: g(-2)=f(f(f(-2)))+2=4>0, g( )=f(f(f(
)=f(f(f(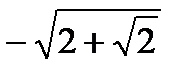 )))+
)))+  =-2+
=-2+  <0. Аналогично рассматриваются другие отрезки. Таким образом, мы нашли восемь отрезков, на которых уравнение f(f(f(x)))=x имеет корни. Следовательно, уравнение f(f(f(x)))=x имеет как минимум восемь корней. Отметим, что функция g(х)=f(f(f(x)))-x является многочленом восьмой степени и более восьми корней уравнение g(х)=0 иметь не может.
<0. Аналогично рассматриваются другие отрезки. Таким образом, мы нашли восемь отрезков, на которых уравнение f(f(f(x)))=x имеет корни. Следовательно, уравнение f(f(f(x)))=x имеет как минимум восемь корней. Отметим, что функция g(х)=f(f(f(x)))-x является многочленом восьмой степени и более восьми корней уравнение g(х)=0 иметь не может.


