
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод введения новых переменных.Содержание книги
Поиск на нашем сайте
Метод введения новых переменных позволяет свести показательное уравнение к алгебраическому уравнению относительно некоторой показательной функции. Рассмотрим несколько примеров. Пример 3. Решим уравнение
Решение. Введём новую переменную: Исходное уравнение принимает вид:
Это квадратное уравнение имеет два корня: Возвращаясь к своей подстановке, получаем: 1) 2) Ответ:
Пример 3. Решим уравнение:
Решение. Так как
Так как
Полагая Возвращаясь к своей подстановке, получаем: 1) 2) Ответ:
4. Функционально-графический метод. Этот метод основан на использовании графических иллюстраций и свойств функций, входящих в уравнение. Рассмотрим несколько примеров. Пример 4. Решим уравнение
Решение. Разделим обе части уравнения на
Левая часть уравнения представляет собой убывающую функцию. Поэтому, если уравнение имеет корень, то он единственный. Очевидно, что Ответ: Пример 5. Решим уравнение
Решение. Перепишем уравнение в виде:
Сравним области значений функций, стоящих в правой и левой частях уравнения. Введём обозначения:
Равенство
Очевидно, Ответ: Пример 6. Решим уравнение
Решение. Преобразуем левую часть уравнения:
Отсюда получаем:
Первое уравнение совокупности корней не имеет. Второе уравнение переписываем в виде:
Так как
Обозначим Уравнение принимает вид: Ответ:
Показательные неравенства. Решение показательных неравенств вида
Теорема 1. Если Теорема 2. Если
Рассмотрим несколько примеров.
Пример 7. Решим неравенство Решение. Так как
решением которого является интервал (-1;7)
Ответ: (-1;7)
Пример 8. Решим неравенство
Решение. Последовательно получаем:
Решаем полученное неравенство методом интервалов и получаем:
Пример 9. Решим неравенство
Решение. Перепишем неравенство в виде Разделим обе части неравенства на
Обозначим
Ответ:
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.005 с.) |


 . Заметим, что
. Заметим, что  .
.
 .
. .
. ;
;

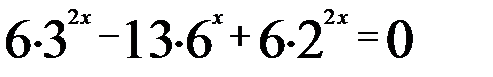 .
. , то имеем:
, то имеем:  .
. ни при каких значениях x не обращается в нуль, то, разделив обе части полученного уравнения на
ни при каких значениях x не обращается в нуль, то, разделив обе части полученного уравнения на  , получаем равносильное уравнение:
, получаем равносильное уравнение: .
.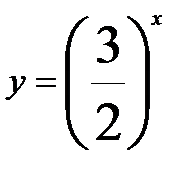 , получаем квадратное уравнение:
, получаем квадратное уравнение: 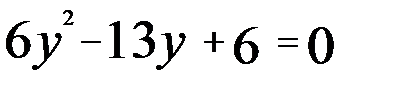 , откуда
, откуда 

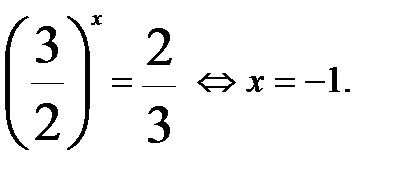

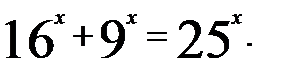
 . Получим уравнение равносильное исходному уравнению:
. Получим уравнение равносильное исходному уравнению: .
. является корнем уравнения.
является корнем уравнения.

 .
. и
и 
 ,
, 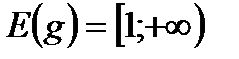
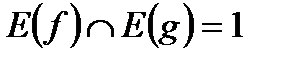 .
. возможно только в случае одновременного выполнения условий:
возможно только в случае одновременного выполнения условий: , то есть
, то есть  .
. .
.
 .
.


 не является корнем уравнения, то разделим обе части уравнения на x. Получаем:
не является корнем уравнения, то разделим обе части уравнения на x. Получаем: .
. и
и 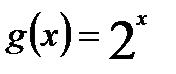 .
. . Функция
. Функция  -- убывающая, функция
-- убывающая, функция  -- возрастающая. Если уравнение имеет корень, то он – единственный. Очевидно, что
-- возрастающая. Если уравнение имеет корень, то он – единственный. Очевидно, что  .
.
 , где
, где  , основано на следующих теоремах:
, основано на следующих теоремах: то неравенство
то неравенство  равносильно неравенству
равносильно неравенству 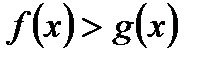 .
. , то неравенство
, то неравенство  равносильно неравенству
равносильно неравенству  .
. .
. , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству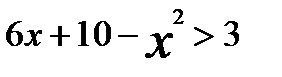 ,
, .
.


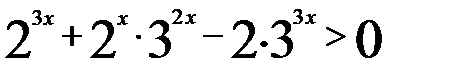 .
. . Так как
. Так как  , получаем
, получаем .
. и получаем неравенство
и получаем неравенство  , из которого имеем
, из которого имеем  . Последовательно получаем:
. Последовательно получаем:





