
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графиков сложных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим сложную функцию y= f [ φ (x)]. Здесь функция y зависит от аргумента x не непосредственно, а через промежуточную функцию φ (x). Обозначив φ (x) через u, получим y= f (u), где u = φ (x). Часто промежуточную функцию u = φ (x) называют внутренней, а функцию y= f (u) – внешней. Графики сложных функций можно строить, учитывая результаты общего исследования функции и используя свойства функций y = f (u) и u = φ (x). При этом надо иметь в виду, что выражение f [ φ (x)] будет иметь смысл для тех значений x, для которых имеет смысл выражение φ (x), и принимать такие значения u, для которых определено выражение f (u). При построении графиков сложных функций следует учитывать основные свойства четных и нечетных функций, периодических функций, монотонных функций. Надо также найти значения сложной функции на концах интервалов монотонности или установить, как ведет себя функция в окрестности этих точек, если они (или одна из них) не принадлежат области определения. Приведем другой способ построения графика сложной функции y= f [ φ (x)] (рис. 14). Обозначим через A, A1, A2, A3, A4 соответственно точки (x; 0), (x; φ (x)), (φ (x); φ (x)), (φ (x); f (φ (x))), (x; f (φ (x))). Построение выполняем в таком порядке: строим графики функций y= f (x) и y = φ (x); проводим биссектрису первого и третьего координатных углов (y = x); проводим через точку A прямую, параллельную оси Оy, до пересечения с графиком функции y = φ (x) (получаем точку A1); проводим через точку A1 прямую, параллельную оси Oх, до пересечения с биссектрисой (получаем точку A2); проводим через точку A2 прямую, параллельную оси Oy, до пересечения с графиком y = f (x) (получаем точку A3); проводим через точку A3 прямую, параллельную оси Ох, до пересечения с продолжением отрезка A, A1. Полученная в пересечении точка A4 (x; f (φ (x))) и будет точкой графика функции y= f [ φ (x)]. Аналогично строятся и остальные точки графика.
Рис. 14 Пользуясь линейкой и циркулем, можно этот способ упростить. Через точку Р (х; 0) проводим перпендикуляр до пересечения с графиком y = φ (x). Получаем точку Q, причем PQ = φ (x). Далее, на оси абсцисс берем точку T с абсциссой ОТ = PQ. Проведя через точку T перпендикуляр до пересечения с графиком y= f (x) в точке S, получим TS = f (x). Проектируя затем точку S на перпендикуляр, проведенный через точку P, получаем точку М (x; f (φ (x))) (рис. 15).
Рис. 15 Замечание. График функции y= f [ φ (x)] можно построить еще и так: строим график функции u = φ (x), а затем, учитывая значения ординат этой функции и основные свойства функции y = f (u), выполняем построение графика заданной функции. Применение графиков функций при решении задач Школьной математики
Задачи с параметрами В зависимости от того, какая роль отводится параметру в задаче (неравноправная или равноправная с переменной), можно соответственно выделить два основных графических приема: первый – построение графического образа на координатной плоскости (x; y), второй – на (x; a). Задача 5. Найти все значения параметра а, при которых уравнение Решение. Переходя к логарифмам по основанию 5, получаем уравнение Построим графики функций
Рис. 16 Ответ: Задача 6. При каких значениях a система уравнений не имеет решений? Решение. Система На рис. 21 точка (3; 0) – центр поворота. Ясно, что если прямая семейства Важно при записи ответа не упустить, что существует еще одна прямая семейства, а именно у = – х + 3, проходящая через «дырки» в гиперболе. Поэтому при а = –1 система также не имеет решений.
Рис. 17 Ответ: а = –1 или Задача 7. При каких значениях параметра а уравнение Решение. Рассмотрим функции у = ах и
иметь одно решение, получим а =
Рис. 18 Итак, прямые семейства у = ах имеют с дугой АВ только одну общую точку при Ответ: Литература 1. Архипов Б.М., Мазаник А.А., Петровский Г.Н., Урбанович М.И. Элементарные функции – Мн: Вышэйшая школа, 1991. 2. Бахтина Т. П. «Таблетки» и «компрессы» при построении графиков. // Математика в школе. – 2004 – №8. 3. Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики. – М.:МЦНМО, 2001. 4. Ершов Л.В., Райхмист Р.Б. Построение графиков функций – М.: Просвещение, 1984.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 4378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |



 имеет решение.
имеет решение. , которое равносильно уравнению
, которое равносильно уравнению 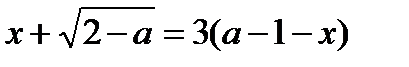 (1), если выполняется условие
(1), если выполняется условие 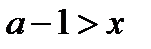 (2). Выражая x из равенства (1) и подставляя в неравенство (2), получаем неравенство
(2). Выражая x из равенства (1) и подставляя в неравенство (2), получаем неравенство 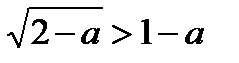 (3). Чтобы решить это неравенство, решим сначала уравнение
(3). Чтобы решить это неравенство, решим сначала уравнение  .
. и
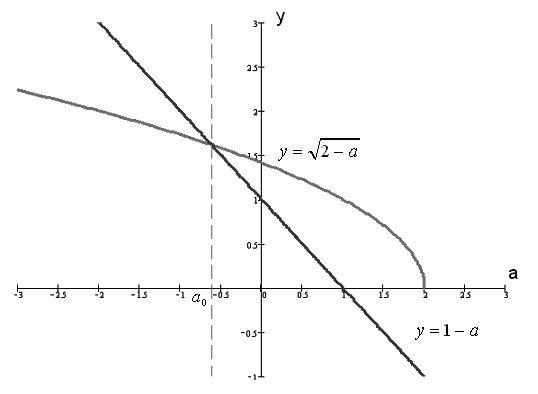
и  (рис. 20). Тогда
(рис. 20). Тогда  – есть решение этого уравнения. Так как мы решаем неравенство
– есть решение этого уравнения. Так как мы решаем неравенство  , тогда решение неравенства
, тогда решение неравенства  .
.

 равносильна исходной.
равносильна исходной. вращается внутри угла OMA, то система не имеет решений. Устанавливаем, что угловой коэффициент прямой MA равен
вращается внутри угла OMA, то система не имеет решений. Устанавливаем, что угловой коэффициент прямой MA равен 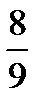 . Тогда при таком повороте параметр a принимает все значения из промежутка (–
. Тогда при таком повороте параметр a принимает все значения из промежутка (–  ; 0]. Заметим, что мы включили a = 0, поскольку прямая MO не пересекает гиперболу.
; 0]. Заметим, что мы включили a = 0, поскольку прямая MO не пересекает гиперболу.
 .
. имеет единственное решение?
имеет единственное решение? . График второй функции легко построить, рассмотрев уравнение (у – 1)2 = 8х— х2 — 15 при у ≥ 1. Преобразовав последнее к виду (у – 1)2 + (х – 4)2 = 1, получаем, что искомый график — полуокружность с центром (4; 1) и радиусом 1. На рис. 22 это дуга АВ. Все прямые у = ах, проходящие между лучами OA и ОВ пересекают дугу в одной точке. Также одну точку с дугой имеют прямая ОВ и касательная ОМ. Легко показать, что угловые коэффициенты прямых ОВ и OA соответственно равны
. График второй функции легко построить, рассмотрев уравнение (у – 1)2 = 8х— х2 — 15 при у ≥ 1. Преобразовав последнее к виду (у – 1)2 + (х – 4)2 = 1, получаем, что искомый график — полуокружность с центром (4; 1) и радиусом 1. На рис. 22 это дуга АВ. Все прямые у = ах, проходящие между лучами OA и ОВ пересекают дугу в одной точке. Также одну точку с дугой имеют прямая ОВ и касательная ОМ. Легко показать, что угловые коэффициенты прямых ОВ и OA соответственно равны 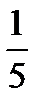 и
и  . Устанавливаем, что угловой коэффициент касательной ОМ равен
. Устанавливаем, что угловой коэффициент касательной ОМ равен  , причем это можно сделать не обязательно при помощи производной. Действительно, потребовав от системы
, причем это можно сделать не обязательно при помощи производной. Действительно, потребовав от системы




