
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ГЛАВА 1. Вычисление значений функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В.И. Перова Т.А. Сабаева
ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ С++
Учебное пособие
Рекомендовано ученым советом механико-математического факультета для студентов ННГУ, обучающихся по направлениям подготовки 080500 «Бизнес-информатика», 010100 «Математика», 010200 «Математика и компьютерные науки», 010400 «Прикладная математика и информатика», 010800 «Механика и математическое моделирование»
Нижний Новгород УДК 681.3.06(075.8) ББК 32.973.26-018.1 П26
П26 Перова В.И., Сабаева Т.А. ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ С++: Учебное пособие. – Нижний Новгород: Изд-во Нижегородского госуниверситета, 2013. – 124 с.
Рецензенты: доктор технических наук, профессор В.Р. Милов кандидат физ.- мат. наук, доцент Н.В. Кротов
В учебном пособии изложены сведения, необходимые для теоретического и практического освоения объектно-ориентированного языка программирования С++. Приведено большое количество реально работающих программ, которые иллюстрируют возможности и особенности языка С++. Информация в учебном пособии расположена в порядке усложнения: от способов написания простых программ, имеющих линейную структуру, до более сложных. Большое внимание уделено таким темам, как вычисление значений функций, суммирование рядов, позиционная запись числа и делители целого числа, сортировка, работа с файлами, построение массивов, обработка последовательности символов, побитовые операции, преобразование и построение матриц, структуры, динамические структуры данных. В конце каждой главы приведены упражнения для самостоятельной работы студентов. Для студентов механико-математического факультета ННГУ, обучающихся по направлениям подготовки 080500 «Бизнес-информатика», 010100 «Математика», 010200 «Математика и компьютерные науки», 010400 «Прикладная математика и информатика», 010800 «Механика и математическое моделирование». Оно призвано оказать помощь всем пользователям, стремящимся к эффективному использованию современных объектно-ориентированных технологий.
Ответственный за выпуск: председатель методической комиссии механико-математического факультета ННГУ, к.ф.-м.н., доцент Н.А. Денисова
УДК 681.3.06(075.8) ББК 32.973.26-018.1
© В.И. Перова, Т.А. Сабаева, 2013
© Нижегородский государственный университет им. Н.И. Лобачевского, 2013 Оглавление
ПРЕДИСЛОВИЕ
В настоящее время резко возрос интерес к программированию. Это связано с развитием и внедрением в повседневную жизнь информационных и коммуникационных технологий [2, 3, 5 – 12, 15, 37]. Все программы, например, компьютерная игра, служебная программа для архивации данных, обозреватель для работы в Интернете или операционная система Windows, написаны на одном или нескольких языках программирования. Сегодня в мире насчитывается около 400 таких языков, которые используются для создания программ, а также еще несколько тысяч языков, давно забытых, или не получивших широкой известности, иногда незаслуженно. К настоящему времени ситуация с использованием различных языков продолжает меняться. Однако для разработки наиболее сложных и высокоэффективных программ используют язык программирования С++ [13, 21 – 23, 27 – 36].
Язык программирования С++ был разработан Бьярном Страуструпом (Bjarne Stroustrup) [29] на основе языка Си [9]. Язык С++ является расширением языка Си, поэтому программы, созданные на языке Си, могут обрабатываться компилятором языка С++. Язык С++ является универсальным языком программирования, так как с его помощью можно решать широкий круг задач, выполняемых на ЭВМ. Язык С++ реализует объектно-ориентированный подход к программированию [14, 16 – 20, 23 – 25]. Он может быть и процедурно-ориентированным, и поддерживать параметрическое программирование. Программы, написанные на языке С++, по быстродействию сравнимы с программами, написанными на Ассемблере. С++ – это язык программирования высокого уровня. Поэтому программы, подготовленные на нем, более наглядны, и они легко переносимы с одного типа компьютера на другой. Материал учебного пособия может быть использован при изучении курсов: «Программирование», «Объектно-ориентированный анализ и программирование (С++)», «Языки и методы программирования», «Технология программирования и работа на ЭВМ», а также при написании курсовых и дипломных работ. Наряду с теоретическим материалом в пособии приведены примеры программ, иллюстрирующих наиболее интересные стороны рассматриваемых вопросов: вычисление значений функций, суммирование рядов, позиционная запись числа и делители целого числа, сортировка данных, построение массивов, работа с файлами, обработка последовательности символов, побитовые операции, преобразование и построение матриц, структуры, динамические структуры данных. В каждой главе учебного пособия приведены упражнения для самостоятельной работы студентов. Учебное пособие предназначено для студентов механико-математического факультета ННГУ, обучающихся по направлению подготовки 080500 «Бизнес-информатика», 010100 «Математика», 010200 «Математика и компьютерные науки», 010400 «Прикладная математика и информатика», 010800 «Механика и математическое моделирование». Оно может быть использовано при изучении языка С++ и студентами других факультетов ННГУ, изучающими объектно-ориентированные технологии. Авторы выражают искреннюю благодарность заведующему кафедрой «Электроника и сети ЭВМ» НГТУ, профессору В.Р. Милову, доценту кафедры численного и функционального анализа ННГУ, доценту Н.В. Кротову за ценные советы при рецензировании рукописи. Авторы выражают искреннюю благодарность за поддержку заместителю по очной форме обучения проректора по учебной работе, заведующей кафедрой прикладной статистики ННГУ, доценту Н.Р. Стронгиной, заведующему кафедрой математического моделирования экономических систем ННГУ, профессору Ю.А. Кузнецову, директору НИИ механики, заведующему кафедрой численного моделирования физико-механических процессов ННГУ, профессору Л.А. Игумнову и директору Института радиоэлектроники и информационных технологий НГТУ, действительному члену Международной академии информатизации, профессору В.Г. Баранову.
ГЛАВА 1. Вычисление значений функций
В отличие от таких языков программирования, как Алгол, Паскаль, Фортран и других, в которых делается различие между программами и подпрограммами, процедурами и функциями, в языке С++ и его предшественнике языке Си используются только функции. При программировании на языке С++ функция является основным понятием, без которого нельзя обойтись. Каждая программа на языке С++ – это совокупность функций. Каждая функция глобальная, т.е. при определенных условиях доступна в модуле либо во всех модулях программы. Каждую из этих функций нужно определить либо описать до её использования в конкретном модуле программы. Программа должна обязательно включать единственную функцию main(),которая является главной функцией [24]. Функция main() обеспечивает создание точки входа в откомпилированную программу. Кроме этой функции в программе может быть любое количество пользовательских функций. Пользовательские функции прямо или опосредованно вызываются из функции main(). При написании функций часто используются операторы циклов.
Операторы циклов
Операторы циклов применяются для организации многократно автоматически повторяющихся вычислений [1, 17, 32]. Любой цикл содержит тело цикла, то есть операторы, которые повторяются несколько раз, начальные установки, модификацию параметров цикла и проверку условия продолжения выполнения цикла. Один проход цикла называется итерацией. На каждой итерации выполняется проверка условия. Проверка условия может выполняться либо до тела цикла (цикл с предусловием), либо после тела цикла (цикл с постусловием). Цикл с предусловием имеет вид:
while (выражение) {операторы тела цикла};
где выражение определяет условие повторения тела цикла. Выражение вычисляется перед каждой итерацией цикла и его тип должен быть арифметическим или приводимым к нему. Выполнение операторов тела цикла начинается с вычисления выражения. Если выражение истинно (true), то операторы тела цикл будут выполняться. Если же при первой проверке выражения оно будет равно false, то цикл не будет выполняться ни разу. Цикл с постусловием записывается в виде:
do {операторы тела цикла} while (выражение);
В данном цикле сначала выполняются операторы тела цикла, то есть простой либо составной операторы, а затем вычисляется выражение. Тип выражения, как и в операторе цикла с предусловием, должен быть арифметическим. Если выражение истинно (true), то операторы тела цикла выполняются ещё раз. Цикл будет завершен, когда выражение будет равным false, либо в теле цикла будет выполнен какой-либо оператор передачи управления. В отличие от цикла с предусловием, в цикле с постусловием операторы тела цикла могут быть выполнены хотя бы один раз.
Кроме указанных выше операторов циклов часто применяется цикл с параметрами. Он имеет следующий вид:
for (инициализация; выражение; шаг) { операторы тела цикла }
где инициализация – используется для объявления присвоения начального значения переменной цикла и присвоения начальных значений другим величинам, которые применяются в цикле. В этой части может быть использована операция «запятая» для задания нескольких операторов, выполняющихся последовательно один за другим. Инициализация осуществляется один раз в начале исполнения цикла. Выражение – определяет условие выполнения цикла. Цикл будет выполняться, если результат выражения, приведенный к типу bool, равен true. Цикл с параметром реализуется как цикл с предусловием. Шаг – предназначен для изменения переменной цикла. В этой части также может быть использована операция «запятая» для задания нескольких операторов. Следует отметить, что любую часть, находящуюся внутри круглых скобок оператора с параметрами for,можно опустить. Однако точки с запятой «;» необходимо оставить на своих местах.
Операторы ветвления
Операторы ветвления используются в разветвленных алгоритмах и служат для выбора маршрута выполнения программы в зависимости от истинности или ложности некоторых условий [1, 17, 32]. Операторы ветвления называют ещё конструкциями принятия решений [1]. К операторам ветвления относятся следующие операторы: условные операторы if, if … else и оператор-переключатель switch. Синтаксис условных операторов имеет вид [1]:
if (выражение) оператор;
либо, если операторов, выполняемых при истинности выражения несколько, то
if (выражение) { оператор 1; оператор 2; ………… оператор N; }
В случае, когда необходимо сравнить выражение с некоторым значением, нужно использовать операции отношений. Например,
if (выражение == значение) оператор; if (выражение!= значение) оператор; if (выражение <= значение) оператор;
Оператор if … else может иметь две ветви:
if (выражение) { оператор 1; оператор 2; } else { оператор 3; оператор 4; }
Здесь вторая ветвь является альтернативой. Оператор if … else допускает применение вложенных конструкций вида:
if (выражение 1) оператор 1; else if (выражение 2) оператор 2; else if (выражение 3) оператор 3; else if (выражение 4) { оператор 4; ………… else if (выражение N) оператор N; else оператор по умолчанию;
где последняя ветвь else оператор по умолчанию; является необязательной. Количество уровней вложенности операторов if может быть любым. Однако при количестве таких вложенных конструкций, больших четырёх-пяти, программу становится трудно отлаживать [1]. Когда в программе нужно выбрать один из многочисленных вариантов, бывает целесообразным применять оператор-переключатель switch. Этот оператор называется ещё оператором множественного выбора [1].
Синтаксис оператора-переключателя switch имеет вид:
Switch (выражение) { case метка 1: оператор 1; break; // Выход из оператора switch { case метка 2: оператор 2; break; ………… case метка N: оператор N; break; default: оператор; } В данном операторе выражение и метки должны иметь значения целого либо символьного типа. Выбирается тот вариант, метка которого совпадает со значением выражения. В случае, когда нет ни одного совпадения меток со значением выражения, выбирается метка default:. Эта метка является необязательной. Упражнения 1. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= log fx (3+ x)3 при x = d+kh, k =0, 1, 2, …, 10; f, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 2. Задана окружность x 2+ y 2= R 2. Определить, лежит ли точка с координатами (x 0, y 0) внутри или вне окружности. Вычислить y= 3. Задана прямая линия ax + by + c =0, причем коэффициенты a и b не равны нулю. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже прямой. Вычислить y= |log3(1+ fx)| при x = d+hk, k =0, 1, 2, …, 10; f, d, h – некоторые числа, если точка лежит выше прямой, и y =0, если точка лежит на прямой линии или ниже прямой. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 4. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y=| (f+mx 2) S/ 2| при x = d+kh, k =0, 1, 2, …, 10; f, S, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 5. Определить, лежит ли точка с координатами (x 0, y 0) в первом квадранте. Вычислить y= ln m /2(1+ x)3 при x = d+kh, k =0, 1, 2, …, 10; m, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне первого квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 6. Определить, лежит ли точка с координатами (x 0, y 0) между параболами y=-x 2+1 и y=x 2-1. Вычислить y= 7. Определить, лежит ли точка с координатами (x 0, y 0) между окружностями радиуса R и r, R > r, с центром в начале координат. Вычислить y= 8. Определить, лежит ли точка с координатами (x 0, y 0) внутри верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 9. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), a – некоторая константа. Вычислить y= 10. Определить, лежит ли точка с координатами (x 0, y 0) внутри нижнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 11. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 12. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), где a – константа. Вычислить y= 13. Определить, лежит ли точка с координатами (x 0, y 0) в третьем квадранте. Вычислить y= 14. Определить, лежит ли точка с координатами (x 0, y 0) вне квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), где a – константа. Вычислить y= 15. Определить, лежит ли точка с координатами (x 0, y 0) вне квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 16. Определить, лежит ли точка с координатами (x 0, y 0) вне верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 17. Определить, лежит ли точка с координатами (x 0, y 0) внутри полосы | y |< с, где c – константа. Вычислить 18. Определить, лежит ли точка с координатами (x 0, y 0) внутри полосы | x |< с, где c – константа. Вычислить 19. Определить, лежит ли точка с координатами (x 0, y 0) между окружностями радиусов R и r, где R > r, с центрами в начале координат. Вычислить y= 20. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= 21. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= 22. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 23. Определить, лежит ли точка с координатами (x 0, y 0) внутри верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 24. Определить, лежит ли точка с координатами (x 0, y 0) во втором квадранте. Вычислить y= 25. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y=
ГЛАВА 2. Суммирование рядов
Основной алгоритм при вычислении суммы ряда
s=0; // Начальное значение суммы ряда Цикл, где s+=a; // a - значение текущего члена ряда
Следует отметить, что значение текущего члена ряда может вычисляться на каждом шаге цикла независимо от значения предыдущего члена суммы или нужно выявить зависимость ai =f (ai -1). Например, если При вычислении сумм могут быть сформулированы следующие задачи [26]. Задано явное выражение функции, представленной данным рядом. Например, ряд
s=
представляет функцию
f (x) = cos(x). (2.2)
Задана точность приближения этой функции рядом s - это d, то есть | f (x) – s| < d. Необходимо выяснить, сколько членов ряда нужно просуммировать, чтобы была достигнута заданная точность. Проводя этот эксперимент необходимо помнить, что при малых значениях точности значение текущего слагаемого должно быть больше минимального допустимого значения данного типа. Провести исследование, как число суммируемых членов зависит от значения точности приближения функции. Второй вариант постановки задачи – это задать значение числа суммируемых членов ряда и оценить погрешность представления функции f (x) конечной суммой этого ряда. Листинг 2.1. Вычислить сумму ряда, заданного формулой (2.1), двумя способами и сравнить результат с функцией (2.2). //L2_1.cpp #include <stdio.h> #include <math.h> // Библиотека математических функций #include <float.h> // Библиотека предельных значений вещественных значений #include <iostream> using namespace std; int main() { setlocale(LC_CTYPE,"russian"); int i,n,m,v; double s,a,delta,f,x; do { cout << "Введите число вычислений "; cin >> m; }while(m <= 0); cout << "Введите x "; cin >> x; f = cos(x); delta = 0.1; cout << " delta n \n"; for(i=0; i<m; i++) { n = 1; s = 1; a = 1; v = 1; while(fabs(s-f) >= delta && fabs(a) > DBL_MIN) { a = a*x*x/(2*n-1)/(2*n); v = -v; s+ = v*a; n++; }
cout.width(7); cout << delta; cout.width(6); cout << n << '\n'; delta/ = 10; } do { cout << "Введите предельное значение n "; cin >> m; }while(m < 0); cout << " delta n \n"; if(n = 0) { delta = fabs(f-s); cout.width(7); cout << delta; cout.width(6); cout << n << '\n'; } else { cout.precision(3); for(n=0; n <= m; n++) { s = 1; a = 1; v = 1; for(i=1; i<=n; i++) { a = a*x*x/(2*i-1)/(2*i); v = -v; s+ = v*a; } delta = fabs(f-s); cout.width(11); cout << delta; cout.width(6); cout << n << '\n'; } } return 0; }
Результат выполнения программы листинга 2.1 представлен на рис. 2.1:
Рис. 2.1. Результат работы программы листинга 2.1
Упражнения
Выполнить упражнения двумя способами [26]: 1. Задана точность приближения этой функции рядом s - это d, то есть | f (x) – s| < d. Необходимо выяснить, сколько членов ряда нужно просуммировать, чтобы была достигнута эта точность. Проводя этот эксперимент, необходимо помнить, что при малых значениях точности значение текущего слагаемого должно быть больше минимального допустимого значения данного типа или число суммируемых членов достигнет предельно допустимого значения. Провести исследование, как число суммируемых членов зависит от значения точности приближения функции. 2. Задать значение числа суммируемых членов и оценить погрешность представления функции f (x) конечной суммой этого ряда.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
Упражнения 1. Среди всех четырехзначных цифр определить число тех, у которых все цифры различны. 2. Найти количество чётных цифр натурального числа N. 3. Найти все натуральные числа, не превосходящие заданного числа N, и делящиеся на каждую из своих цифр. 4. Найти все натуральные числа, не превосходящие заданного числа N, десятичная запись которых есть строго возрастающая или строго убывающая последовательность цифр. 5. Найти все пары двухзначных натуральных чисел M и N, таких, что значение произведения M×N не изменится, если в числах изменить порядок цифр. Например, M =38 и N =83. 6. Найти все натуральные числа, не превосходящие заданного числа N, сумма квадратов цифр которых кратна 13. 7. Найти все четырехзначные числа 8. Сложить все цифры какого-либо натурального числа, затем все цифры полученной суммы и так далее до тех пор, пока не получится цифра, которая называется корнем данного числа (например, число 34697, тогда 3+4+6+9+7=29, 2+9=11, 1+1=2). Найти корень заданного натурального числа. 9. Среди трехзначных натуральных чисел найти такие числа, у которых сумма цифр, сложенная с квадратом этой суммы, равна исходному числу. 10. Определить пятизначное число N такое, что шестизначные числа 11. Определить трехзначное число, удовлетворяющее условию: удалив старшую цифру и умножив полученное число на 7, получаем исходное число. 12. Натуральное число N называется числом Армстронга, если сумма цифр, каждая из которых возведена в степень, равную числу цифр в N, равна исходному числу. Найти все числа Армстронга, заключенные между числами N 1 и N 2. 13. Найти все автоморфные числа в промежутке от N 1 до N 2. Автоморфным называется число, квадрат которого заканчивается этим же числом. Например, число 25 и его квадрат 625. 14. Найти натуральные числа- палиндромы в диапазоне от N 1 до N 2. Например, число 1246421 является палиндромом. 15. Определить k -ю цифру последовательности 123456789101112131415…, в которой подряд записаны все натуральные числа. 16. Определить k -ю цифру последовательности 1101001000010000…, в которой подряд записаны степени числа 10. 17. Определить k -ю цифру последовательности 1392781243729…, в которой подряд записаны степени числа 3. 18. Определить k -ю цифру последовательности 1491625364964…, в которой подряд записаны все квадраты натуральных чисел. 19. Определить k- ю цифру последовательности 182764125216343…, в которой подряд записаны все кубы натуральных чисел. 20. Проверить, является ли заданное число палиндромом. Если это не палиндром, то заменить порядок цифр на обратный и сложить с исходным числом. Если полученное число не является палиндромом, то операцию повторять до тех пор, пока не получится число-палиндром. Для натуральных числе в диапазоне от N 1 до N 2 определить максимальное число действий преобразования числа в палиндром. 21. Найти все трехзначные числа, которые при увеличении на 1 делятся на 2, при увеличении на 2 делятся на 3, при увеличении на 3 делятся на 4, а при увеличении на 4 делятся на 5. 22. Найти все трехзначные числа, квадраты которых оканчиваются исходным числом. 23. Найти все трехзначные числа, сумма цифр которого и само число кратны 7. 24. Из натурального числа удалить все цифры от 0 до 3, оставив прежним порядок остальных цифр. 25. Среди всех трехзначных чисел найти такие, что исходное число равно среднему арифметическому всех чисел (включаяя и исходное число). Число состоит из тех же цифр,т.е.
Упражнения 1. Для натурального числа N найти сумму всех делителей, включая 1 и само число. 2. Для натурального числа N найти число четных делителей. 3. Для натурального числа N найти число всех делителей, исключая 1 и само число. 4. Для натур
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.102 (0.011 с.) |

 при x = d+kh, k =0, 1, 2,…, 10; m, f, d, h – некоторые числа, если точка лежит вне окружности, и y = x, если точка лежит внутри окружности или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2,…, 10; m, f, d, h – некоторые числа, если точка лежит вне окружности, и y = x, если точка лежит внутри окружности или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.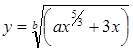 при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y =0, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y =0, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в третьем квадранте, и y = x 2, если точка вне третьего квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в третьем квадранте, и y = x 2, если точка вне третьего квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2+ ax, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2+ ax, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xa, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xa, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.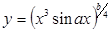 при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xb +1, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xb +1, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2,…,10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2,…,10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне второго квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне второго квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. – это к значению объекта, содержащего текущее значения суммы, добавляется значение текущего члена суммы, причем начальное значение суммы полагается равным нулю. Например,
– это к значению объекта, содержащего текущее значения суммы, добавляется значение текущего члена суммы, причем начальное значение суммы полагается равным нулю. Например, , n= 0, 1, …, то an =an -1× x 2/(2 n -1)/2 n. Для этого примера следует отметить ещё одну особенность: при n = 0 значение a 0=1, так как 0!=1, то есть слагаемое a 0 необходимо присвоить значению объекта s до выполнения цикла.
, n= 0, 1, …, то an =an -1× x 2/(2 n -1)/2 n. Для этого примера следует отметить ещё одну особенность: при n = 0 значение a 0=1, так как 0!=1, то есть слагаемое a 0 необходимо присвоить значению объекта s до выполнения цикла. . (2.1)
. (2.1)






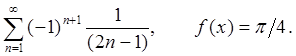













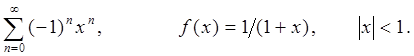

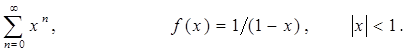
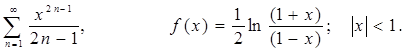

 , для которых справедливо
, для которых справедливо  .
. и
и  связаны соотношением
связаны соотношением 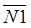 =3×
=3×  .
. .
.


