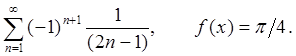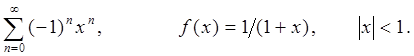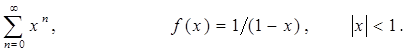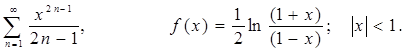Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы, необходимые для написания программСодержание книги Поиск на нашем сайте
Обратим внимание на то, что при написании программ необходимо иметь в виду следующие алгоритмы, которые встречаются и при вычислении значений функций. 1) Ограничение на входные данные приводит к необходимости проверки при их введении. Для этого можно использовать следующие циклы.
а) цикл с предусловием while (условие).... Условие должно принимать значение «истина» при неправильном вводе данных. Например, необходимо ввести натуральное число n. Это осуществляется следующим циклом с предусловием:
cin >> n; while (n <= 0) { cout << ”Введите натуральное число “; cin >> n; }
б) цикл с постусловием do... while (условие). Условие должно принимать значение «истина» при неправильном вводе данных. Например, необходимо ввести натуральное число n. Это осуществляется следующим циклом с постусловием:
do { cout << ”Введите натуральное число “; cin >> n; }while (n <= 0);
2) Следует помнить о необходимости проверки аргументов функций, если область определения функции отлична от всего пространства. 3) Еще один часто встречающийся алгоритм при вводе данных – необходимо ввести n элементов массива x[i], значения которого уникальны. Это можно осуществить с помощью следующего цикла с параметрами:
for(i=0; i<n; i++) { cout << "Введите x("<<i+1<<") = "; cin >> x[i]; for(j=0; j<i; j++) if(x[i] == x[j]) // Если встретился такой же элемент, { // необходимо его ввести вновь, i--; // причем его индекс будет повторяться break; // до тех пор, пока значение не будет } // уникальным. }
Листинг 1.1. Задана прямая линия ax + by + c =0, причем коэффициенты a и b не равны нулю (необходимо проверить при вводе). Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже прямой. Вычислить y= ln(5+3 x) при x = d+hk, k =0, 1, 2, …, 10, если точка лежит выше прямой, и y =0, если точка лежит на прямой линии или ниже ее. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
//stdafx.h #pragma once #define WIN32_LEAN_AND_MEAN #include <stdio.h> #include <math.h> // Библиотека математических функций #include <tchar.h> #include <iostream> using namespace std; // Использовать пространство имен std
//L1_1.cpp #include “stdafx.h” int main() { setlocale(LC_CTYPE, “russian”); // Функции обработки символов double x,y,a,b,c; do // Контроль того, что a и b не равны нулю { cout << «Введите коэффициенты прямой a b c «; cin >> a >> b >> c; }while(a == 0 || b == 0); cout << «Введите начальную точку и шаг «; cin >> d >> h; cout << ’\n’; cout << «x y Результат\n\n»; cout.precision(5); // Вывод 5 значащих цифр for(i=0; i<=10; i++) { x=d+i*h; if(5+3*x <= 0) { cout.width(32); // Выводить в 32 позициях cout << «Функцию вычислить нельзя\n»; } else { y=log(5+3*x); if(a*x+b*y+c<0) { cout.width(4); // Выводить в 4 позициях cout << x; cout.width(8); // Выводить в 8 позициях cout << y; cout << «Точка лежит под прямой \n»; } else { cout.width(4); // Выводить в 4 позициях cout << x; cout.width(8); // Выводить в 8 позициях cout << 0; cout << «Точка лежит над прямой \n»; } } } return 0; }
Результат работы программы листинга 1.1 приведен на рис. 1.1:
Рис. 1.1. Результат работы программы листинга 1.1
Упражнения 1. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= log fx (3+ x)3 при x = d+kh, k =0, 1, 2, …, 10; f, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 2. Задана окружность x 2+ y 2= R 2. Определить, лежит ли точка с координатами (x 0, y 0) внутри или вне окружности. Вычислить y= 3. Задана прямая линия ax + by + c =0, причем коэффициенты a и b не равны нулю. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже прямой. Вычислить y= |log3(1+ fx)| при x = d+hk, k =0, 1, 2, …, 10; f, d, h – некоторые числа, если точка лежит выше прямой, и y =0, если точка лежит на прямой линии или ниже прямой. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 4. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y=| (f+mx 2) S/ 2| при x = d+kh, k =0, 1, 2, …, 10; f, S, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 5. Определить, лежит ли точка с координатами (x 0, y 0) в первом квадранте. Вычислить y= ln m /2(1+ x)3 при x = d+kh, k =0, 1, 2, …, 10; m, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне первого квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. 6. Определить, лежит ли точка с координатами (x 0, y 0) между параболами y=-x 2+1 и y=x 2-1. Вычислить y= 7. Определить, лежит ли точка с координатами (x 0, y 0) между окружностями радиуса R и r, R > r, с центром в начале координат. Вычислить y= 8. Определить, лежит ли точка с координатами (x 0, y 0) внутри верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 9. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), a – некоторая константа. Вычислить y= 10. Определить, лежит ли точка с координатами (x 0, y 0) внутри нижнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 11. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 12. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), где a – константа. Вычислить y= 13. Определить, лежит ли точка с координатами (x 0, y 0) в третьем квадранте. Вычислить y= 14. Определить, лежит ли точка с координатами (x 0, y 0) вне квадрата с координатами вершин (a; a), (a; - a), (- a; - a), (- a; a), где a – константа. Вычислить y= 15. Определить, лежит ли точка с координатами (x 0, y 0) вне квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 16. Определить, лежит ли точка с координатами (x 0, y 0) вне верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 17. Определить, лежит ли точка с координатами (x 0, y 0) внутри полосы | y |< с, где c – константа. Вычислить 18. Определить, лежит ли точка с координатами (x 0, y 0) внутри полосы | x |< с, где c – константа. Вычислить 19. Определить, лежит ли точка с координатами (x 0, y 0) между окружностями радиусов R и r, где R > r, с центрами в начале координат. Вычислить y= 20. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= 21. Задана парабола y = ax 2 +bx+c. Определить, лежит ли точка с координатами (x 0, y 0) выше или ниже параболы. Вычислить y= 22. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y= 23. Определить, лежит ли точка с координатами (x 0, y 0) внутри верхнего полукруга радиуса R с центром в начале координат, где R – константа. Вычислить 24. Определить, лежит ли точка с координатами (x 0, y 0) во втором квадранте. Вычислить y= 25. Определить, лежит ли точка с координатами (x 0, y 0) внутри квадрата с координатами вершин (a; 0), (0; - a), (- a; 0), (0; a), где a – константа. Вычислить y=
ГЛАВА 2. Суммирование рядов
Основной алгоритм при вычислении суммы ряда
s=0; // Начальное значение суммы ряда Цикл, где s+=a; // a - значение текущего члена ряда
Следует отметить, что значение текущего члена ряда может вычисляться на каждом шаге цикла независимо от значения предыдущего члена суммы или нужно выявить зависимость ai =f (ai -1). Например, если При вычислении сумм могут быть сформулированы следующие задачи [26]. Задано явное выражение функции, представленной данным рядом. Например, ряд
s=
представляет функцию
f (x) = cos(x). (2.2)
Задана точность приближения этой функции рядом s - это d, то есть | f (x) – s| < d. Необходимо выяснить, сколько членов ряда нужно просуммировать, чтобы была достигнута заданная точность. Проводя этот эксперимент необходимо помнить, что при малых значениях точности значение текущего слагаемого должно быть больше минимального допустимого значения данного типа. Провести исследование, как число суммируемых членов зависит от значения точности приближения функции. Второй вариант постановки задачи – это задать значение числа суммируемых членов ряда и оценить погрешность представления функции f (x) конечной суммой этого ряда. Листинг 2.1. Вычислить сумму ряда, заданного формулой (2.1), двумя способами и сравнить результат с функцией (2.2). //L2_1.cpp #include <stdio.h> #include <math.h> // Библиотека математических функций #include <float.h> // Библиотека предельных значений вещественных значений #include <iostream> using namespace std; int main() { setlocale(LC_CTYPE,"russian"); int i,n,m,v; double s,a,delta,f,x; do { cout << "Введите число вычислений "; cin >> m; }while(m <= 0); cout << "Введите x "; cin >> x; f = cos(x); delta = 0.1; cout << " delta n \n"; for(i=0; i<m; i++) { n = 1; s = 1; a = 1; v = 1; while(fabs(s-f) >= delta && fabs(a) > DBL_MIN) { a = a*x*x/(2*n-1)/(2*n); v = -v; s+ = v*a; n++; }
cout.width(7); cout << delta; cout.width(6); cout << n << '\n'; delta/ = 10; } do { cout << "Введите предельное значение n "; cin >> m; }while(m < 0); cout << " delta n \n"; if(n = 0) { delta = fabs(f-s); cout.width(7); cout << delta; cout.width(6); cout << n << '\n'; } else { cout.precision(3); for(n=0; n <= m; n++) { s = 1; a = 1; v = 1; for(i=1; i<=n; i++) { a = a*x*x/(2*i-1)/(2*i); v = -v; s+ = v*a; } delta = fabs(f-s); cout.width(11); cout << delta; cout.width(6); cout << n << '\n'; } } return 0; }
Результат выполнения программы листинга 2.1 представлен на рис. 2.1:
Рис. 2.1. Результат работы программы листинга 2.1
Упражнения
Выполнить упражнения двумя способами [26]: 1. Задана точность приближения этой функции рядом s - это d, то есть | f (x) – s| < d. Необходимо выяснить, сколько членов ряда нужно просуммировать, чтобы была достигнута эта точность. Проводя этот эксперимент, необходимо помнить, что при малых значениях точности значение текущего слагаемого должно быть больше минимального допустимого значения данного типа или число суммируемых членов достигнет предельно допустимого значения. Провести исследование, как число суммируемых членов зависит от значения точности приближения функции. 2. Задать значение числа суммируемых членов и оценить погрешность представления функции f (x) конечной суммой этого ряда.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 при x = d+kh, k =0, 1, 2,…, 10; m, f, d, h – некоторые числа, если точка лежит вне окружности, и y = x, если точка лежит внутри окружности или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2,…, 10; m, f, d, h – некоторые числа, если точка лежит вне окружности, и y = x, если точка лежит внутри окружности или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.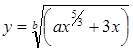 при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y =0, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y =0, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в третьем квадранте, и y = x 2, если точка вне третьего квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в третьем квадранте, и y = x 2, если точка вне третьего квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = сx 2 + bx, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2+ ax, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2+ ax, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xa, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xa, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.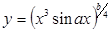 при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xb +1, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = xb +1, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 + x, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2,…,10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2,…,10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y = x, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; f, m, d, h – некоторые числа, если точка лежит выше параболы, и y =0, если точка находится ниже параболы или на ней. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне второго квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; a, b, d, h – некоторые числа, если точка лежит в первом квадранте, и y = x 2, если точка находится вне второго квадранта. Вывести на экран дисплея информацию, если функцию вычислить нельзя. при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя.
при x = d+kh, k =0, 1, 2, …, 10; с, b, d, h – некоторые числа, если точка лежит в этой области, и y = x 2 +2, если точка находится вне области. Вывести на экран дисплея информацию, если функцию вычислить нельзя. – это к значению объекта, содержащего текущее значения суммы, добавляется значение текущего члена суммы, причем начальное значение суммы полагается равным нулю. Например,
– это к значению объекта, содержащего текущее значения суммы, добавляется значение текущего члена суммы, причем начальное значение суммы полагается равным нулю. Например, , n= 0, 1, …, то an =an -1× x 2/(2 n -1)/2 n. Для этого примера следует отметить ещё одну особенность: при n = 0 значение a 0=1, так как 0!=1, то есть слагаемое a 0 необходимо присвоить значению объекта s до выполнения цикла.
, n= 0, 1, …, то an =an -1× x 2/(2 n -1)/2 n. Для этого примера следует отметить ещё одну особенность: при n = 0 значение a 0=1, так как 0!=1, то есть слагаемое a 0 необходимо присвоить значению объекта s до выполнения цикла. . (2.1)
. (2.1)