
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ГЛАВА 7. Обработка последовательности символовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При обработке последовательности символов наиболее часто используются следующие три алгоритма [26]:
§ алгоритм выделения слова из строки; § выбор слов, подходящих под шаблон; § перевод прописных символов в строчные.
Алгоритм выделения слова из строки
Алгоритм выделения слова из строки заключается в нахождении индекса, соответствующего началу слова (первый не пробельный символ), и индекса первого после окончания слова пробела или признака конца строки (символ ‘\0’). Существование слова гарантируется отличной от нуля разностью между вторым и первым символом. Листинг 7.1. Определить число слов в тексте, записанном в файле. //L7_1.cpp #include <fstream> #include <iostream> using namespace std; int sum_word(char*st);//Прототип функции int main() { int sum=0; char s[81]; fstream f("input.txt"),f1; f.getline(s,80); // Читаем строку из файла while(!f.eof()) // Проверка достижения конца файла { sum+=sum_word(s); // Добавляем в сумму число // слов в текущей строке. f.getline(s,80); // Чистим следующую строку } f.close(); f1.open("input.txt",ios::app); // Открываем файл для пополнения f1<<"\n\nЧисло слов в тексте = "<<sum<<'\n'; f1.close(); return 0; } // Функция, определяющая число слов в строке: int sum_word(char *st) { int s=0,b,e=0; while(st[e]!= '\0') { // Пропускаем ведущие пробелы: while(st[e]!= '\0' && st[e] == ' ') e++; b=e; // Пропускаем символы слова: while(st[e]!= '\0' && st[e]!=' ') e++; if(e-b>0) // Слово выделено s++; } return s; }
Результат работы программы листинга 7.1 приведен на рис. 7.1.
В файле с именем “input.txt” содержится информация о количестве чисел и сами числа. Необходимо сформировать массив, не содержащий повторяющихся значений. Этот алгоритм был рассмотрен в главе 1. При работе с файлом он выглядит следующим образом.
Число слов в тексте = 35
Рис. 7.1. Результат работы программы листинга 7.1
Выбор слов, подходящих под шаблон
Выбор слов, подходящих под шаблон, является одним из наиболее применяемых алгоритмов. Например, задано слово, в котором встречаются символы ‘*’ и ‘?’. Такие слова будем называть шаблоном. Если в произвольном слове символы совпадают с символами шаблона, а вместо символа ‘*’ можно использовать любую последовательность символов и вместо ‘?’ – любой символ, то говорят, что слово подходит под шаблон. Например, пароход и паропровод подходят под шаблон паро*од. В первом случае под ‘*’ скрывается последовательность “х”, а во втором – “пров”. Под шаблон ?а?а подходят слова мама и папа. Листинг 7.2. Функция shablon () проверяет, подходит ли слово под шаблон вида ‘*’.
//L7_2.cpp int shablon(char *word, char *sh) { int b, e, si=0, ls; while(sh[si]!= '\0' && sh[si]!= '*') si++; // Если символ ‘*’ отсутствует: if(si == strlen(sh) && strcmp(word, sh) == 0) return 1; if(si == strlen(sh) && strcmp(word, sh)!= 0) return 0; // si – индекс символа ‘*’ в шаблоне. // Проверяем совпадение до ‘*’: for(b=0; b<si; b++) if(word[b]!= sh[b]) break; if(b<si) // Символы не совпали return 0; else { // Проверяем совпадение после ‘*’: for(e=strlen(word)-1, ls = strlen(sh)-1; sh[ls]!= '*'; e--, ls--) if(word[e]!= sh[ls]) break; if(sh[ls]!= '*') // Символы не совпали с символом ‘*’ return 0; else // Символы совпали до и после ‘*’ return 1; }
Перевод прописных символов в строчные
При обработке последовательности символов также часто используется процедура – перевод символов верхнего регистра (прописные символы) в символы нижннего регистра (строчные символы). Листинг 7.3. Функция A_to_a () переводит прописные символы в строчные.
//L7_3.cpp
char A_to_a(char c) { if(c >='А' && c <= 'Я') c = c + 'а ' - 'А'; return c; }
Упражнения 1. В файле задан текст. Определить количество слов в тексте, которые начинаются и заканчиваются на одну и ту же букву. 2. В файле задан текст. Создать массив из уникальных слов в тексте, подходящих под заданный шаблон, включающий в себя символы “?”. 3. В файле задан текст. Определить количество слов в тексте, которые являются палиндромами. Слово называется палиндромом, если чтение слева направо и справа налево дает один и тот же результат. Строчные и прописные буквы не различать. 4. В файле задан текст. Создать массив из уникальных слов в тексте, подходящих под заданный шаблон, включающий в себя символы “*”. 5. В файле задан текст. Определить количество строк в тексте, которые являются палиндромами, если игнорировать пробелы. Строчные и прописные буквы не различать. 6. Используя функцию из раздела 7.3, которая переводит прописные буквы в строчные буквы, преобразовать текст, находящийся в файле. 7. Написать функцию, определяющую число гласных букв в слове. В тексте, записанном в файле, определить слово с максимальным числом гласных букв. 8. Написать функцию, определяющую число гласных букв в слове. В тексте, записанном в файле, определить слово с минимальным числом гласных букв. 9. В файле задан текст. Написать функцию, определяющую длину слова. С помощью этой функции определить количество слов в тексте, имеющих заданную длину. Найденные слова записать в выходной файл. 10. В файле задан текст. Написать функцию, определяющую длину слова. С помощью этой функции определить слова максимальной длины. Найденные слова записать в исходный файл. 11. В файле задан текст. Создать массив из слов этого текста, являющихся палиндромами, которые подходят под заданный шаблон, включающий в себя символы “?”. 12. В файле задан текст. Записать в новый файл четные строки исходного текста с указанием их номера в исходном тексте. 13. В файле задан текст. Написать функцию, определяющую длину слова. Применяя эту функцию, в выходной файл записать слова с указанием их длины. 14. В файле задан текст. Написать функцию, определяющую длину слова. С помощью этой функции определить, сколько слов в тексте имеют длину, больше заданной длины. Найденные слова записать в выходной файл. 15. В файле задан текст. Написать функцию, определяющую длину слова. С помощью этой функции определить, сколько слов в тексте имеют длину, меньше заданной длины. Найденные слова записать в выходной файл. 16. В файле задан текст. Определить строки, количество слов в которых совпадает с заданным числом. Найденные строки записать в выходной файл с указанием их номера в исходном файле. 17. В файле задан текст. Определить строки, количество слов в которых меньше заданного числа. Найденные строки записать в выходной файл с указанием их номера в исходном файле. 18. В файле задан текст. Определить строки, количество слов в которых больше заданного числа. Найденные строки записать в выходной файл с указанием их номера в исходном файле. 19. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘?’. Определить число слов в тексте файла, которые подходят под заданный шаблон. 20. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘*’. Определить число слов в тексте файла, которые подходят под заданный шаблон. 21. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘*’. Найти слова в тексте файла, подходящие под заданный шаблон, и имеющие длину меньше заданной. 22. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘*’. Найти слова в тексте файла, подходящие под заданный шаблон, и имеющие длину больше заданной. 23. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘?’. Найти слова в тексте файла, подходящие под заданный шаблон, и имеющие длину меньше заданной. 24. В файле задан текст. Написать функцию, определяющую, подходит ли слово под заданный шаблон, содержащий символ ‘?’. Найти слова в тексте файла, подходящие под заданный шаблон, и имеющие длину, больше заданной. 25. Написать функцию, определяющую длину слова. В тексте, записанном в файле, определить число слов с нечетным числом букв. Найденные слова с указанием их длины записать в выходной файл.
ГЛАВА 8. Побитовые операции
Побитовые операции можно применять только к целочисленным операндам типа char, short, int, long. Они действуют на отдельные разряды двоичного представления чисел. В С++ определены следующие побитовые операции [32]:
| – побитовое логическое ИЛИ; & – побитовое логическое И; ^ – побитовое исключающее ИЛИ; ~ – побитовое логическое отрицание; << – сдвиг влево; >> – сдвиг вправо.
Результаты действия побитовых операций на операнды a и b представлены в табл. 8.1.
Таблица 8.1 Побитовые операции
Операция побитового логического отрицания (~) является унарной. В результате этой операции каждый бит, имеющий значение 1, становится равным 0 и наоборот. Данная операция называется также дополнением до единицы или инверсией. Результатом операции сдвига влево (<<) является левый операнд, сдвинутый влево на число позиций, которое указано в правом операнде. Освобождающиеся младшие разряды заполняются нулями [24, 25]. Данная операция может применяться для умножения на число, равное степени числа 2, в соответствии с правилом:
x << n эквивалентно умножению х на 2 в степени n.
Результатом операции сдвига вправо (>>) является левый операнд, сдвинутый вправо на число позиций, которое указано в правом операнде. Освобождающиеся старшие разряды заполняются нулями для переменных типа unsigned либо значением старшего (знакового) бита для данных другого типа [24, 25]. Данная операция может применяться для деления на число, равное степени числа 2, в соответствии с правилом:
x >> n эквивалентно делению х на 2 в степени n.
Следует отметить, что перед выполнением побитовых операций нужно преобразовывать знаковые целые числа в беззнаковые целые. Листинг 8.1. Для печати содержимого памяти, отведенной под переменную типа unsigned int,может быть использована функция, в которой создается массив, и элементы массива заполняются следующим образом: § Создается шаблон, содержащий единицу в старшем разряде. § Проверяется побитовое умножение исходного числа на шаблон и в массив заносится символ ‘1’, если это произведение отлично от нуля, и ‘0’ – в противном случае. § Затем шаблон сдвигается вправо на один бит. § Для более легкого чтения информации после каждых 8 битов в массив заносится пробел. § Операция повторяется до тех пор, пока шаблон отличен от нуля.
//L8_1.cpp void print_bit(unsigned int x) { unsigned int sh=~0, i=0, k=0; sh=~(sh>>1); // Шаблон с 1 в старшем разряде char s[40]; while(sh>0) { s[i++]=sh&x?'1':'0'; k++; if(k==8) { s[i++]=' '; k=0; } sh>>=1; // Сдвиг шаблона в следующий разряд } s[i]='\0'; cout<<s<<'\n'; }
Для успешной проверки данной функции следует вводить числа в шестнадцатеричном виде, так как каждая шестнадцатеричная цифра представляется четырьмя двоичными разрядами. Листинг 8.2. Программа печатает двоичное представление числа с использованием функции, приведенной в листинге 8.1.
//L8_2.cpp #include <fstream> #include <iostream> using namespace std; int main() { setlocale(LC_CTYPE,"russian"); unsigned int n; do { cout<<"Введите неотрицательное n "; cin>>hex>>n; // Ввол числа в шестнадцатеричной // системе счисления. }while(n<0); print_bit(n); // Печать числа в двоичной системе числения cin.get(); cin.get(); return 0; }
Результат работы программы листинга 8.2 приведен на рис. 8.1.
Рис. 8.1. Результат работы программы листинга 8.2
Листинг 8.3. В заданном числе инвертировать n битов с позиции k вправо. При вводе данных следует контролировать, чтобы позиция инвертируемого бита и количество инвертируемых битов не выходили за пределы числа. Для построения необходимо создать шаблон, содержащий 1 в инвертируемых позициях и 0 в остальных.
//L8_3.cpp #include <stdio.h> #include <tchar.h> #include <iostream> using namespace std; void print_bit(unsigned int x);
int main() { setlocale(LC_CTYPE,"russian"); unsigned int x, n, k, m, sh, y; m=sizeof(unsigned int)*8; do { cout<<"Введите неотрицательное x "; cin>>hex>>x; }while(x<0); do { cout<<"Введите позицию k и число инвертируемых битов n "; cin>>dec>>k>>n; }while(!(k<=m&&n<=k)); print_bit(x); sh=~0; sh=((sh<<m-k)>>m-n)<<k-n; y=~(x&sh)&sh; x=x&(~sh)|y; print_bit(x);
return 0; }
void print_bit(unsigned int x) { unsigned int sh=~0,k=0,i=0; char s[40]; sh=~(sh>>1); cout<<'\n'; while(sh!=0) { s[i++]=(sh&x)?'1':'0'; k++; if(k%8==0) s[i++]=' '; sh=sh>>1; } s[i]='\0'; cout<<s<<'\n'; }
На рис. 8.2 приведен результат выполнения программы листинга 8.3.
Рис. 8.2. Результат работы программы листинга 8.3
Побитовые операции можно использовать для укрупненного начертания слов. Укрупненное начертание какого-либо символа связано с заданием этого символа в виде таблицы [15]. Заполненные клетки таблицы образуют нужный контур символа. Содержимое такой таблицы можно закодировать с помощью 1 (клетка заполнена) и 0 (клетка не заполнена). Пусть такая таблица состоит из 7 × 5 элементов. Тогда для идентификации символа достаточно пяти семиразрядных двоичных чисел. Каждое из них будет кодировать один из пяти вертикальных слоев. Например, начертание символа “ Н” кодируется следующими двоичными числами: 1111111 (первый и пятый вертикальные слои таблицы), 10 (второй, третий и четвертый слои таблицы). При этом переход от младших разрядов к старшим соответствует просмотру исходной таблицы сверху вниз (рис. 8.3).
Рис. 8.3. Кодирование начертания символа “ Н ”
Для распечатки символа необходимо установить, какие двоичные цифры находятся в соответствующих разрядах всех пяти чисел: 0 – печатать пробел, 1 – печатать выбранный символ. Листинг 8.4. Вывести на экран дисплея укрупненное начертание слов: “ННГУ” и “МЕХМАТ”. //L8_4.cpp #include "stdafx.h" #include <stdio.h> #include <locale> void _tmain() {setlocale (LC_ALL, "Russian"); int i, j, k, n; int B[6][5], D[6][5]; static char s[]="ННГУ", s2[]="МЕХМАТ"; char c, e; for (n=0; (c=s[n])!='\0'; n++) switch (c) { case 'Н': B[n][0]=B[n][4]=0177; B[n][1]=B[n][2]=B[n][3]=010; break;
case 'Г': B[n][0]=0177; B[n][1]=B[n][2]=B[n][3]=01; B[n][4]=03; break;
case 'У': B[n][0]=047; B[n][1]=B[n][2]=B[n][3]=0110; B[n][4]=077; break; } for (k=0; k<7; k++) // k – разряд { for (i=0; i<n; i++) // i – буква { j=0; // j - слой do {if (B[i][j] & 01) // Выделение k-го разряда каждого // из чисел, кодирующих букву. printf("%c", s[i]); else printf("%c", ' '); B[i][j]=B[i][j]>>1; // Сдвиг вправо на одну позицию // всех разрядов числа. j++; } while (j<5); printf("%s", " "); } printf ("\n"); } printf ("\n"); for (n=0; (e=s2[n])!='\0'; n++) switch (e) { case 'М': D[n][0]=D[n][4]=0177; D[n][1]=D[n][3]=02; D[n][2]=04; break;
case 'Е': D[n][0]=0177; D[n][1]=D[n][2]=D[n][3]=0111; D[n][4]=0101; break;
case 'Х': D[n][0]=D[n][4]=0143; D[n][1]=D[n][3]=024; D[n][2]=010; break;
case 'А': D[n][0]=D[n][4]=0176; D[n][1]=D[n][2]=D[n][3]=011; break;
case 'Т': D[n][0]=D[n][1]=D[n][3]=D[n][4]=01; D[n][2]=0177; break; } for (k=0; k<7; k++) { for (i=0; i<n; i++) { j=0; do { if (D[i][j] & 01) // Выделение k-го разряда каждого // из чисел, кодирующих букву. printf("%c", s2[i]); else printf("%c", ' '); D[i][j] = D[i][j] >> 1; // Сдвиг вправо на одну позицию // всех разрядов числа. j++; } while (j<5); printf("%s", " "); } printf ("\n"); } printf ("\n"); }
Результат выполнения программы листинга 8.4 приведен на рис. 8.4.
Рис. 8.4. Результат работы программы листинга 8.4
Упражнения 1. Написать функцию, заменяющую n правых битов числа x на n правых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 2. Написать функцию, заменяющую n левых битов числа x на n правых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 3. Написать функцию, заменяющую n правых битов числа x на n правых инвертированных битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 4. Написать функцию, которая циклически перемещает n правых битов числа х в старшие биты, не меняя их порядка. Провести вычисление для заданного числа x и заданного количества правых битов n. Результат записать в файл. 5. Написать функцию, заменяющую n левых битов числа x на n правых битов этого же числа. Провести вычисление для заданного числа x и заданного количества левых битов n. Результат записать в файл. 6. Написать функцию, заменяющую n левых битов числа x на инвертированные n левых битов этого числа. Провести вычисление для заданного числа x и заданного количества левых битов n. Результат записать в файл. 7. Написать функцию, заменяющую n левых битов числа x на n левых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 8. Написать функцию, заменяющую n битов с позиции p числа x на n правых инвертированных битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 9. Написать функцию, заменяющую n левых битов числа x на n правых инвертированных битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 10. Написать функцию, которая циклически перемещает n левых битов числа х в младшие биты, не меняя их порядка. Провести вычисление для заданного числа x и заданного количества правых битов n. Результат записать в файл. 11. Написать функцию, заменяющую n левых битов числа x на инвертированные n правых битов этого числа. Провести вычисление для заданного числа x и заданного количества левых битов n. Результат записать в файл. 12. Написать функцию, заменяющую n правых битов числа x на инвертированные n правых битов этого числа. Провести вычисление для заданного числа x и заданного количества правых битов n. Результат записать в файл. 13. Написать функцию, определяющую количество единиц в двоичном представлении целого числа. Провести вычисление для заданного числа х. Результат записать в файл. 14. Написать функцию, определяющую разность между количеством нулей и единиц в двоичном представлении целого числа. Провести вычисление для заданного числа х. Результат записать в файл. 15. Написать функцию, заменяющую n битов с позиции p числа x на n правых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 16. Написать функцию, заменяющую n битов с позиции p числа x на n левых инвертированных битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 17. Написать функцию, заменяющую n битов с позиции p числа x на инвертированные. Провести вычисление для заданного числа x и заданного количества битов n. Результат записать в файл. 18. Написать функцию, определяющую количество нулей в двоичном представлении целого числа. Провести вычисление для заданного числа х. Результат записать в файл. 19. Написать функцию, заменяющую n битов с позиции p числа x на n левых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 20. Написать функцию, заменяющую n битов с позиции p числа x на n правых битов числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 21. Написать функцию, определяющую количество битов, значение которых в двоичном представлении чисел x и y совпадают. Провести вычисление для заданных чисел x и y. Результат записать в файл. 22. Написать функцию, определяющую количество битов, значение которых в двоичном представлении чисел x и y не совпадают. Провести вычисление для заданных чисел x и y. Результат записать в файл. 23. Написать функцию, определяющую разность между количеством единиц в двоичном представлении чисел x и y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 24. Написать функцию, определяющую разность между количеством нулей в двоичном представлении чисел x и y. Провести вычисление для заданных чисел x и y. Результат записать в файл. 25. Написать функцию, заменяющую n левых битов числа x на n битов с позиции p числа y. Провести вычисление для заданных чисел x и y. Результат записать в файл.
ГЛАВА 9. Преобразование и построение матриц
Матрица – это прямоугольная таблица, образованная из элементов некоторого множества и состоящая из n строк и m столбцов [16]:
Такая таблица называется прямоугольной матрицей размера (n×m) или (n ×m)-матрицей с элементами При работе с матрицами следует обратить внимание на то, определены или нет размеры матрицы до начала выполнения программы. Рассмотрим два случая выделения памяти под элементы матрицы.
§ Размерность матрицы определена перед выполнением программы
Если размерность матрицы задана заранее, например ее размерность равна 8, то используется описание:
Тип имя_матрицы [8][8];
В этом случае происходит статическое выделение памяти, то есть память выделяется до выполнения программы. При объявлении указанного объекта создается указатель с именем имя_матрицы, выделяется место под 8 указателей типа * Тип и адрес первого байта становится значением переменной Действия операционной системы может быть схематически отображено следующим образом (рис. 9.1):
Рис. 9.1. Иллюстрация статического выделения памяти под элементы матрицы
§ Размерность матрицы не определена перед выполнением программы
Поскольку размеры матрицы не определены до начала выполнения программы, следует использовать динамическое выделение памяти под элементы матрицы, то есть выделение памяти во время выполнения программы. Если размерность матрицы заранее неизвестна, то для ее описания используется указатель типа указатель на * Тип.
Тип ** имя_матрицы;
В этом случае создается только переменная имя_матрицы типа Тип**. Когда определено число строк (n) и число столбцов (m) матрицы, с помощью операции new выделяется место под n переменных типа Тип*:
имя_матрицы = new Тип* [n];
то есть создается массив имя_матрицы [i]. Затем, для каждого элемента имя_матрицы [i] с помощью той же операции new выделяется место под n элементов типа Тип. Окончательно это может быть оформлено в виде следующего фрагмента:
Тип** имя_матрицы; имя_матрицы = new Тип* [n]; for(i=0; i<m; i++) имя_матрицы [i] = new Тип [m];
Иными словами, проводятся те операции, которые в первом случае выполняет операционная система.
При преобразовании и построении матриц целесообразно выполнять следующие действия: а) Размерность матрицы и значение ее элементов необходимо читать из файла, так как для ввода с клавиатуры это слишком большой объем информации. б) Печать матрицы следует оформить в виде отдельной функции, причем оформить шаблонную функцию для того, чтобы можно было печатать матрицы любого типа.
В определении шаблона функций применяется служебное слово template. Для параметризации используется список формальных параметров, который заключается в угловые скобки < >. Каждый формальный параметр шаблона обозначается служебным словом class, за которым следует имя параметра (идентификатор). Каждый параметр обязательно должен присутствовать в заголовке функции. При обращении к функции формальные параметры заменяются фактическими параметрами соответствующего типа. Листинг 9.1. В программе из файла с именем “input.txt” читаются две матрицы размером 3 × 5. Одна из них вещественная, а другая целочисленная. Причем у вещественной матрицы оставляется только два знака после запятой с округлением.
//L9_1.cpp #include «stdafx.h» // Файлы, помещенные в данный файл заголовка, будут // предварительно откомпилированы. #include <fstream> #include <iostream> using namespace std; // Прототип шаблонной функции можно записать в две строки: template <class pp> // Введение параметров шаблона void print_matrix(pp **a, int n, int m);
int _tmain() // Компилятор создаст либо функцию main(), либо функцию // wmain() в зависимости от установок UNICODE. { setlocale(LC_CTYPE,"russian"); int n,m,i,j; double **A; // Указатель, который будет связан // с матрицей А. ifstream ff("input.txt"); ff>>n>>m; A=new double*[n]; // Идентификация указателя А и запрос // памяти под n указателей типа double*. for(i=0; i<n; i++) A[i]=new double[m]; // Идентификация указателя А[i] и запрос //памяти под m указателей типа double. for(i=0; i<n; i++) for(j=0; j<m; j++) ff>>A[i][j]; cout<<"Исходная матрица\n"; print_matrix(A,n,m); int **X; // Указатель, который будет связан с //матрицей X. X=new int*[n]; // Идентификация указателя X и запрос //памяти под n указателей типа int*. for(i=0; i<n; i++) X[i]=new int[m]; // Идентификация указателя X[i] и запрос // памяти под m указателей типа int. for(i=0;i<n;i++) for(j=0;j<m;j++) ff>>X[i][j]; ff.close(); cout<<"Исходная целочисленная матрица матрица\n"; print_matrix(X,n,m); cin.get(); return 0; } template <class pp> // Заголовок шаблонной функции void print_matrix(pp **a,int n,int m) // можно записать в две строки. { int i,j; for(i=0;i<n;i++) { for(j=0;j<m;j++) { cout.width(8); int y=int(a[i][j] * 1000); if(y % 10 > 5) y=y/10+1; else { if(y % 10 == 5 && y % 2!= 0) y=y/10+1; else y/=10; } cout<<double(y) / 100; } cout<<'\n'; } }
На рис. 9.2 представлен результат выполнения программы листинга 9.1.
Рис. 9.2. Результат работы программы листинга 9.1
Листинг 9.2. Пусть задана матрица A размером n × n. Необходимо построить матрицу B размером n × n, причем элементы матрицы определяются следующим образом: по индексам i и j строится область W, в которой
Рис. 9.3. Вид области W для построения матрицы В
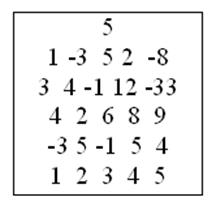
Содержимое файла “input.txt”
Рис. 9.4. Исходные данные для построения матрицы В
//L9_2.cpp #include <fstream> #include <iostream> using namespace std; double** bild_matr(double**, int); // Прототип функции bild_matr() void print_matr(double**, int); // Прототип функции print_matr() int main() { double **A, **B; int i, j, n; setlocale(LC_CTYPE, "russian"); ifstream fin("input.txt"); fin >> n; A=new double *[n]; for(i=0;i<n;i++) A[i]=new double[n]; for(i=0;i<n;i++) for(j=0;j<n;j++) fin>>A[i][j]; cout<<"Исходная матрица\n"; print_matr(A,n); B=bild_matr(A,n); cout<<"Полученная матрица\n"; print_matr(B,n); cin.get(); return 0; } void print_matr(double**A, int n) { int i,j; for(i=0;i<n;i++) { for(j=0;j<n;j++) { cout.width(5); cout<<A[i][j]; } cout<<'\n'; } } double** bild_matr(double**A, int n) { int i, j, k, l; double **B; B=new double*[n]; for(i=0;i<n;i++) B[i]=new double[n]; for(i=0; i<n; i++) for(j=0; j<n; j++) { B[i][j]=A[i][j]; for(k=0; k<=i; k++) for(l=j-i+k;l<=j+i-k;l++) if(l>=0 && l<n && B[i][j]<A[k][l]) B[i][j]=A[k][l]; } return B; }
Результат выполнения программы листинга 9.2 приведен на рис. 9.5.
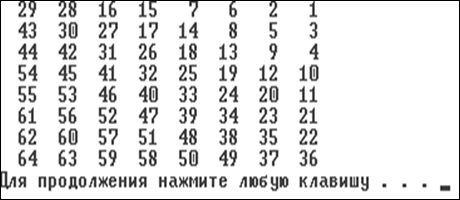
Рис. 9.5. Результат работы программы листинга 9.2 Листинг 9.3. Пусть задан массив из 64 целых чисел. Будем считать, что одномерный массив состоит из целых чисел от 1 до 64. Построить матрицу размером 8 × 8 из данного одномерного массива, вставляя элементы одномерного массива в матрицу согласно схеме (рис. 9.6) [26].
Рис. 9.6. Схема размещения элементов одномерного массива в матрице
//L9_3.cpp #include <iostream> using namespace std; int main() { int A[8][8], C[64]; int i, j, k, l=0; // Переменная l принимает значение 0 при //движении по схеме на рис. 9.6 вниз и значение 1 //при движении вверх. for(i=0;i<64;i++) C[i]=i+1; for(i=0;i<=7;i++) { if(i%2!=0) for(k=0,j=7-i;k<=i;k++,j++) { A[k][j]=C[l]; l++; } else for(k=i,j=7;k>=0;k--,j--) { A[k][j]=C[l]; l++; } } for(i=1;i<=7;i++) { if(i%2!=0) for(k=7,j=7-i;j>=0;k--,j--) { A[k][j]=C[l]; l++; } else for(k=i,j=0;k<=7;k++,j++) { A[k][j]=C[l]; l++; } } for(i=0; i<8; i++) { for(j=0; j<8; j++) { cout.width(4); cout<<A[i][j]; } cout<<'\n'; } return 0; }
Результат выполнения программы листинга 9.3 приведен на рис. 9.7.
Рис. 9.7. Результат работы программы листинга 9.3
Листинг 9.4. В программе создается квадратная единичная матрица, порядок которой вводится с клавиатуры. Память под элементы матрицы выделяется динамически во время выполнения программы. Динамически выделенная память освобождается оператором delete [24].
//L9_4.cpp #include "stdafx.h" #include <iostream> #include <locale> using namespace std; void _tmain() {setlocale (LC_ALL,"Russian"); int n; int i, j; cout<<"Введите порядок матрицы: \n"; cin>>n; float **matr; matr=new float *[n]; if(matr==NULL) {cout<<"\n Не создан динамический массив"; return; } for(i=0; i<n; i++) {matr[i]=new float [n]; if(matr[i]==NULL) {cout<<"\n Не создан динамический массив"; return; } for(j=0; j<n; j++) if(i!=j) matr[i][j]=0; else matr[i][j]=1; } for(i=0; i<n; i++) {cout<<"\n Строка "<<i+1<<":"; for(j=0; j<n; j++) cout<<'\t'<<matr[i][j]; } for(i=0; i<n; i++) delete matr[i]; delete [] matr; }
Результат выполнения программы листинга 9.4 представлен на рис. 9.8.
Рис. 9.8. Результат работы программы листинга 9.4
Листинг 9.5. В программе создается матрица, элементы которой задаются случайным образом. Память под элементы матрицы выделяется динамически во время выполнения программы. Программа состоит из трех функций: str() – функция вычисления среднего значения по строкам матрицы, stlb() – функция вычисления среднего значения по столбцам матрицы и функция _tmain().
//L9_5.cpp #include "stdafx.h" #include <stdio.h> #include <locale> #include <iostream> #include <stdlib.h> #include <conio.h> using namespace std;
double* str (int** arr, int n, int m) { double* res = new double [n]; double k = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { k += arr[i][j]; } res[i] = k / m; k = 0; } return res; } double* stlb (int** arr, int n, int m) { double* res = new double [m]; double k = 0; for (int j = 0; j < m; j++) { for (int i = 0; i < n; i++) { k += arr[i][j]; } res[j] = k / n; k = 0; } return res; } int _tmain() { setlocale(LC_ALL, "Russian"); int n, m; cout << "Введите количество строк: "; cin >> n; cout << "\n"; cout << "Введите количество столбцов: "; cin >> m; cout << "\n"; int** arr; arr = new int*[n]; for (int i = 0; i < n; i++) { arr[i] = new int[m]; } for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { arr[i][j] = rand() % 10; } } cout<<"Матрица: \n"<<endl; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { cout << arr[i][j]; cout << " "; } cout << "\n"; } cout<<endl; double* sr_stroki = str(arr, n, m); cout << "Среднее значение по строкам: \n"<<endl; for (int i = 0; i < n; i++) { cout << sr_stroki[i] << " "; } cout << '\n'; cout<<endl; double* sr_stolb = stlb(arr, n, m); cout << "Среднее значение по столбцам: \n"<<endl; for (int i = 0; i < m; i++) { cout << sr_stolb[i] << " "; } cout << '\n'; return 0; }
На рис. 9.9 представлен результат выполнения программы листинга 9.5.
Рис. 9.9. Результат работы программы листинга 9.5
Упражнения 1. В файле “input.txt” задана матрица А размером n × m. В первой строке файла указаны ее размеры (n и m), а в следующих строках файла – значения элементов матрицы по строкам. Построить вектор 2. В файле “input.txt” задана матрица А размером n × m. В первой строке файла указаны ее размеры (n и m), а в следующих строках файла – значения элементов матрицы по строкам. Построить вектор 3. В файле “input.txt” задана квадратная матрица А размером n × n. В первой строке файла указан ее размер (n), а в сл
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.144 (0.013 с.) |



 1
1
 1
1
 1
1

 (9.1)
(9.1)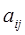 . Элемент
. Элемент 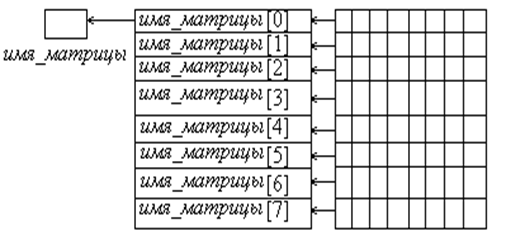

 . Область W показана на рис. 9.3 [26]. Индексы k и l изменяются в этом случае в следующих пределах: k от 0 до i, а l от j – i + k до j + i - k, причем при проведении сравнения с элементом akl следует проверять, что l лежит в диапазоне от 0 до n -1. Исходные данные находятся в файле “input.txt”, представленном на рис. 9.4.
. Область W показана на рис. 9.3 [26]. Индексы k и l изменяются в этом случае в следующих пределах: k от 0 до i, а l от j – i + k до j + i - k, причем при проведении сравнения с элементом akl следует проверять, что l лежит в диапазоне от 0 до n -1. Исходные данные находятся в файле “input.txt”, представленном на рис. 9.4.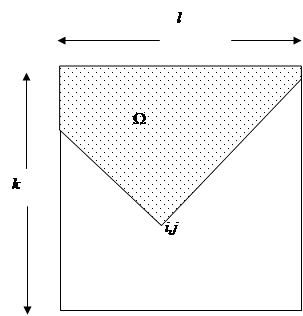




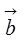 размерности n, причем bi определяется как максимальное значение в i -ой строке матрицы. Исходную матрицу и полученный вектор записать в файл.
размерности n, причем bi определяется как максимальное значение в i -ой строке матрицы. Исходную матрицу и полученный вектор записать в файл.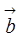 размерности n, причем bi определяется как сумма значений в i-ой строке матрицы. Исходную матрицу и полученный вектор записать в файл.
размерности n, причем bi определяется как сумма значений в i-ой строке матрицы. Исходную матрицу и полученный вектор записать в файл.


