
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень, наименование, обозначение символов и отображаемые ими функцииСодержание книги
Поиск на нашем сайте
Кафедра «информатика»
Алгоритмы в блок-схемах
Методические указания к выполнению лабораторной работы для студентов по направлениям 190000, 200000, 260000, 280000 специальностей 140211, 150202, 151001, 150002, 19201, 190601, 190603, 190702, 200503, 260601, 280101
Курган 2006
Кафедра: «Информатика»
Дисциплина: «Информатика» (направления: 190000, 200000, 260000, 280000 специальности: 140211, 150202, 151001, 150002, 19201, 190601, 190603, 190702, 200503, 260601, 280101)
Составили: старший преподаватель Сысолятина Л.Г. старший преподаватель Бекишева М.Б.
Методические указания составлены на основе учебных программ по указанному курсу. Работа выполнена при равноценном участии авторов.
Утверждены на заседании кафедры «25» мая 2006 г., протокол № 8
Рекомендованы методическим советом Курганского государственного университета «____» _______________ 2006 г. Введение Прежде чем обратиться к рассмотрению конкретных алгоритмов, необходимо определиться с тем, что же такое алгоритм. Традиционно считается, что самый первый алгоритм был придуман древнегреческим математиком Евклидом – правило нахождения общего делителя двух целых чисел. В современной математике понятие алгоритма является ключевым понятием, которое восходит к работам выдающегося узбекского математика IX века Аль-Хорезми. Примеры алгоритмов в широком смысле этого слова можно встретить и в повседневной жизни. Так, поваренная книга является сборником алгоритмов, описывающих процессы приготовления пищи. Не случайно термин «рецепт» часто можно встретить как синоним термину алгоритм. Компьютерные программы представляют собой алгоритмы, записанные средствами языков программирования. Алгоритм и его свойства Исчерпывающее определение алгоритма дано выдающимся соотечественником А. А Марковым. алгоритм – это точное общепринятое предписание, определяющее процесс преобразования исходных данных в искомый результат. Исполнитель алгоритма -это тот объект или субъект, для управления которым составлен алгоритм. Система команд исполнителя (СКИ) - это вся совокупность команд, которые исполнитель умеет выполнять. Алгоритм должен обладать следующими свойствами: понятностью, точностью, конечностью. Понятность: алгоритм составляется только из команд, входящих в СКИ исполнителя. Точность: каждая команда алгоритма управления определяет однозначное действие исполнителя. Конечность (или результативность): выполнениеалгоритма должно приводить к результату за конечное число шагов. Среда исполнителя: обстановка, в которой функционирует исполнитель. Определенная последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления блюда по кулинарному рецепту нужны соответствующие продукты (данные). Для решения математической задачи (решение квадратного уравнения) нужны исходные числовые данные (коэффициенты уравнения). Полный набор данных: необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата).
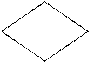
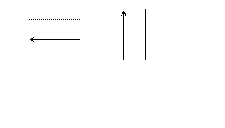
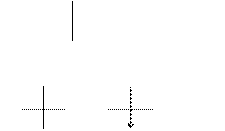
для того чтобы сделать алгоритм более наглядным, часто используют блок-схемы. Блок-схема алгоритма представляет собой систему блоков, соединенных между собой линиями, которые указывают последовательность выполнения блоков. Направление на линии связи между блоками указывается стрелкой в конце линии. Если линия связи направлена сверху вниз и слева направо, то стрелка на этой линии не ставится. Блоки изображаются геометрическими фигурами, внутри которых дается текстоформульная информация. Блок, организующий ввод или вывод данных, изображается параллелограммом. Для изображения разветвления используется ромб, внутри которого записывается разветвление. для обозначения начала и конца алгоритма используются прямоугольники с закругленными углами. Допускается нумерация блоков путем разрыва верхней стороны их контура и записи на месте разрыва номера блока. При составлении блок-схемы алгоритма рекомендуется располагать ее на одной странице ученической тетради и придерживаться правил, установленных ГОСТ 19.002-80 «Схемы алгоритмов и программ. Правила выполнения» и ГОСТ 19.003-80 «Схемы алгоритмов и программ. Обозначения условные графические». Фрагменты ГОСТ 19.002-80 Единая система программной документации Схемы алгоритмов и программ Правила выполнения
Настоящий стандарт распространяется на алгоритмы и программы систем программного обеспечения вычислительных машин, комплексов и систем независимо от их назначения и области применения и устанавливает правила выполнения схем алгоритмов и программ, выполняемых автоматическим способом или от руки. Стандарт полностью соответствует МС ИСО 2636-73.
Правила выполнения схем 1.1.1. При выполнении схем алгоритмов и программ отдельные функции алгоритмов и программ, с учетом степени их детализации, отображаются в виде словных графических обозначений – символов по ГОСТ 19.003-80. 1.1.2. Для облегчения вычерчивания и нахождения на схеме зон устанавливают с учетом минимальных размеров символов, изображенных на данном листе. Допускается один символ размещать в двух и более зонах, если размер символа превышает размер зоны. 1.1.3. Координаты зоны представляют: по горизонтали – арабскими цифрами слева направо в верхней части листа; по вертикали – прописными буквами латинского алфавита сверху вниз в левой части листа. 1.1.4. Координаты зон в виде сочетания букв и цифр присваиванию символам, вписанным в поля этих зон, например А1, А2, А3, В1, В2, В3 и т.д. При выполнении схем от руки, если поле листа не разбито на зоны, символам присваивают порядковые номера. 1.1.5. В пределах одной схемы, при выполнении ее от руки, допускается применять не более двух смежных размеров ряда чисел, кратных 5. 1.1.6. Расположение символов на схеме должно соответствовать требованиям ГОСТ 19.003-80. 1.1.7. Линии потока должны быть параллельны линиям внешней рамки схемы. 1.1.8. Направления линии потока сверху вниз и слева направо принимают за основные и, если линии потока не имеют изломов, стрелками можно не обозначать. В остальных случаях направление линии потока обозначать стрелкой обязательно. 1.1.9. Расстояние между параллельными линиями потока должны быть не менее 3 мм, между остальными символами схемы – не менее 5 мм. 1.1.10. Записи внутри символа или рядом с ним должны быть краткими. Сокращения слов и аббревиатуры, за исключением установленных государственными стандартами, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится. 1.1.11. Для удобства детализации программы должны быть использованы символы «Процесс», «Решение», «Модификация», «Ввод-вывод» и «Пуск-останов», при этом внутри символов на расстоянии не менее 0,25 а проводят тонкую линию (размер а по ГОСТ 19.003-80) 1.1.12. Записи внутри символов должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока (черт. 1) Вид а должен быть прочитан как вид б.
А б Рис. 1 Правила применения символов 1.2.1. Применение символов должно соответствовать указанному в табл. 1. Таблица 1
Фрагменты ГОСТ 19.003-80 Единая система программной документации Схемы алгоритмов и программ Обозначения условные графические Настоящий стандарт распространяется на условные графические обозначения (символы) в схемах алгоритмов и программ, отображающие основные операции процесса обработки данных и программирования для систем программного обеспечения вычислительных машин, комплексов и систем независимо от их назначения и области применения. Стандарт не распространяется на записи и обозначения, помещаемые внутри символа или рядом с ним, служащие для уточнения выполненных им функций. Стандарт устанавливает перечень, наименования, форму, размеры символов и отображаемые символами функции.
Линейный алгоритм Алгоритм, в котором команды выполняются последовательно одна за другой, называется линейным алгоритмом. Линейный алгоритм может быть построен из команд присваивания, ввода и вывода.
Пример: x:=5 Переменной X присваивается значение, равное 5.
Пример: ввод А - ввод значения переменной А с клавиатуры компьютера.
Пример: вывод Х - значение переменной Х выводится на экран. На блок-схеме хорошо видна структура линейного алгоритма, по которой исполнителю (человеку) удобно отслеживать процесс его выполнения.
Повторять <тело цикла>
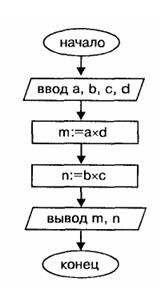
Примеры Пример 1. Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления. Решение. В алгебраической форме решение задачи выглядит следующим образом:
Тест: a = 3, b=4, c=5, d=6. Результат: m = 18, n = 20.
Пример 2. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Обмен происходит через промежуточную переменную Z.
Z:=X X:=Y
вывод X, Y
Тест: x = 3, y = -7.
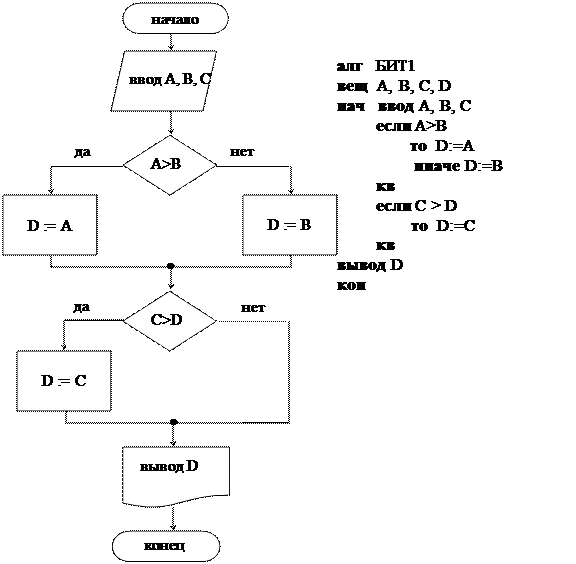
Пример 3. Даны три вещественных числа А, В, С. Найти наибольшее среди них. Решение.1 способ. Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух последовательных ветвлений.
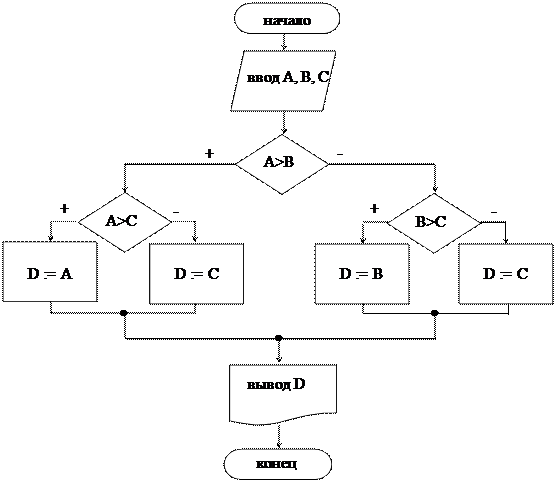
Тест: a = 3, b = 6, c = 2. Результат: D = 6. 2 способ. Задача решена с помощью вложенных ветвлений.
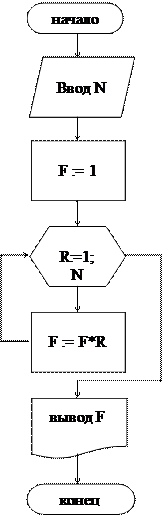
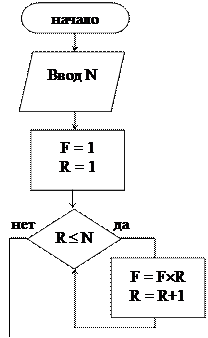
Пример 4. Дано целое положительное число N. Вычислить факториал этого числа: N! = 1 * 2 * 3 *... * N Решение. Задача решается c помощью циклического алгоритма. Составим два варианта алгоритма: цикла с параметром и с применением цикла с предусловием.
Тест: N = 5. Результат: факториал F = 120.
Пример 5. вычислить значение функции Y = A = BX + CX2 для
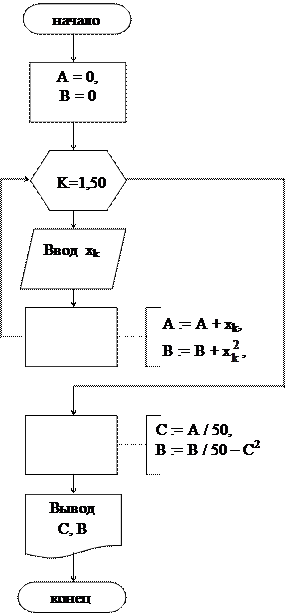
Пример 6. Вычислить выборочное среднее С и выборочную дисперсию D случайной величины x по формулам
(х1, х2, …, х50 – выборочные значения случайной величины х). Указание: при нахождении суммы (произведения) рекомендуется начальное значение суммы (произведения) брать равным нулю (единице) или первому слагаемому (множителю).
Пример 7. Использование вложенных циклов на примере вычисления двойной суммы
А= В = (b1, b2, b3, …, bk) – одномерный массив (вектор) данных одного и того же типа.
Варианты Задание по лабораторной работе «Алгоритмы в блок-схемах» Составить алгоритмы на уровне блок-схем решения задач 5.1., 5.2., 5.3., 5.4., 5.5., 5.6. Контроль решения задачи или тест или ожидаемый результат должен быть рассмотрен и подготовлен до решения задачи с помощью ЭВМ. Номер варианта указывает преподаватель. Задачи на линейный алгоритм 5.1.1. Вычислить объем конуса и площадь основания. Даны радиус основания R и высота конуса H. (V= 5.1.2. Вычислить радиус вписанного в треугольник круга по сторонам треугольника.
5.1.3. Даны два числа. Найти их сумму, произведение и разность. 5.1.4. Дано t. Камень бросили в колодец, и через t секунд послышался всплеск воды. На какой глубине (от сруба) вода в колодце. (h= g*t2/2) 5.1.5.Составить программу вычисления площади треугольника по его трем углам A, B, C и стороне a. 5.1.6.Вычислить площадь поверхности цилиндра по радиусу основания R и высоте цилиндра H. 5.1.7.Дана сторона куба. Вычислить объем куба и полную поверхность. 5.1.8.Даны площадь треугольника S и стороны a, b, c. Вычислить сумму его высот. 5.1.9.Вычислить радиус описанного круга по сторонам треугольника. 5.1.10.Вычислить площадь трапеции по ее основаниям и высоте. 5.1.11.Длины сторон первого прямоугольника a и b, его площадь в 6 раз меньше площади второго прямоугольника. Найти длину стороны второго прямоугольника, если длина одной из его сторон равна c. 5.1.12.Составить алгоритм вычисления площади треугольник со сторонами a, b, c (а, b, c - вещественные положительные числа). 5.1.13.Длина стороны треугольника равна a, периметр равен Р, длины двух других сторон равны между собой. Найти эти длины. 5.1.14.Периметр треугольника рaвен Р, длина одной стороны равна a, другой - b. Найти длину третьей cтоpоны. 5.1.15.Найти полную поверхность конуса с высотой H и радиусом основания R Задачи на разветвление 5.2.1. Написать алгоритм нахождения максимального среди четырех целых чисел. 5.2.2. Написать алгоритм проверки условия: имеются ли среди трех целых чисел два положительных числа? 5.2.3. Написать алгоритм проверки условия: могут ли три данных числа быть длинами сторон треугольника? 5.2.4. Написать алгоритм проверки условия: лежит ли данная точка c координатами (х, у) в первой четверти координатной плоскости? 5.2.5. Проверить принадлежность числа x интервалам [а,b] или [c,d]. 5.2.6. Проверить, является ли четырехугольник со сторонам a, b, c, d ромбом. 5.2.7. Определить, является ли треугольник со сторонами а, b, c равнобедренным. 5.2.8. Определить, является ли треугольник со сторонами а, b, c равносторонним. 5.2.9. Среди чисел а, b, с определить количество отрицательных. 5.2.10. Среди чисел а, b, с определить количество положительных. 5.2.11. Числа а и b - катеты одного треугольника, с и d - катеты другого. Определить являются ли эти треугольники равновеликими. 5.2.12. Определить, принадлежит ли заданная точка (х,у) плоской фигуре, являющейся кольцом с центром в начале координат, с внутренним радиусом r1 и внешним радиусом r2. 5.2.13. Какая площадь больше - параллелограмма со сторонами а, b и углом между ними 30° или площадь прямоугольника со сторонами n, m? 5.2.14. Выбрать среди данных четырех чисел a, b, c, d те, которые принадлежат интервалу (m, n). 5.2.15. Сколько чисел среди а, b, c, d принадлежит отрезку [m, n]. Задачи на двумерные массивы
5.6.1. Дана действительная матрица размера m*n. Найти сумму наибольших значений элементов ее строк. 5.6.2. Дана действительная матрица размера m*n. Найти сумму наибольших значений элементов ее столбцов. 5.6.3. В данной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный. 5.6.4. В данной квадратной матрице порядка n найти сумму элементов столбцов, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный. 5.6.5. Дана целочисленная квадратная матрица порядка n. Найти номера строк, все элементы которых – нули. 5.6.6. Дана целочисленная квадратная матрица порядка n. Найти номера строк, элементы в каждой из которых одинаковы. 5.6.7. Дана целочисленная квадратная матрица порядка n. Найти номера строк, все элементы которых – четны. 5.6.8. Дана действительная квадратная матрица порядка n. Создать массив номеров столбцов с отрицательными элементами на главной диагонали. 5.6.9. Дана действительная квадратная матрица порядка n. Создать массив номеров строк с отрицательными элементами на главной диагонали. 5.6.10. Дана действительная матрица размера m*n. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов. 5.6.11. Дана целочисленная квадратная матрица порядка n. Выяснить, имеются ли в матрице ненулевые элементы, и если имеются, то указать номера этих элементов. 5.6.12. Дана целочисленная матрица порядка m*n. Найти матрицу, получающуюся из данной перестановкой столбцов – первого с последним. 5.6.13. Дана действительная матрица размера m*n. Найти произведение наибольших значений элементов ее строк, если они не нулевые. 5.6.14. Дана действительная матрица размера m*m. Найти разность наибольших значений элементов ее столбцов и соответствующих этим столбцам диагональных элементов. 5.6.15. В данной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент со значением, принадлежащим интервалу (1; 5). Предполагается, что такой элемент единственный. Список ЛИТЕРАТУРы
1. Информатика: Базовый курс: Учебник для вузов / Под ред. С. В. Симоновича. – СПб.: Питер, 2003. С 640. 2. Угринович Н. Информатика и информационные технологии. М.: Бином, Лаборатория знаний, 2003. С.512. 3. Семакин И.Г., Вараксин Г. С. Информатика. Структурированный конспект базового курса. М.: Лаборатория базовых знаний, 2004. С.168. 4. Семакин И.Г., Хеннер Е. Информатика: Задачник – практикум. Т.1. М.: Лаборатория базовых знаний, 2002. С.304. 5. ГОСТ 19.002-80. Единая система программной документации. Схемы алгоритмов и программ. Правила выполнения. 6. ГОСТ 19.003-80. Единая система программной документации. Схемы алгоритмов и программ. Обозначения условные графические.
содержание
Введение. 3 Алгоритм и его свойства. 3 1. Фрагменты ГОСТ 19.002-80. 5 1.1. Правила выполнения схем. 5 1.2. Правила применения символов. 7 2. Фрагменты ГОСТ 19.003-80. 11 2.1. Перечень, наименование, обозначение символов и отображаемые ими функции 11 2.2. Соотношение геометрических элементов символов. 14 3. основные типы алгоритмических структур. 15 3.1. Линейный алгоритм. 15 3.2. Алгоритмическая структура «Ветвление». 15 3.3. Алгоритмическая структура «Выбор». 17 3.4. Алгоритмическая структура «Цикл». 17 4. Примеры.. 19 5. Варианты.. 28 5.1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.018 с.) |

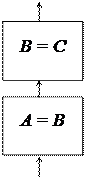
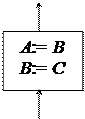





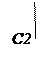















 А
А








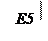


 Е5
Е5




 В1
В1 А
А

 А
А





 5
5










 =
=
 y1 011E1
y1 011E1 y2 016A1
y2 016A1 y3 005B5
y3 005B5 y1 015E4
y1 015E4
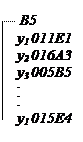



 координата символа
координата символа номер листа схема
номер листа схема Команда ввода - команда, по которой значения переменных задаются через устройства ввода (например, клавиатуру).
Команда ввода - команда, по которой значения переменных задаются через устройства ввода (например, клавиатуру). Команда вывода: команда, по которой значение величины отражается на устройстве вывода компьютера (например, экран дисплея, бумага).
Команда вывода: команда, по которой значение величины отражается на устройстве вывода компьютера (например, экран дисплея, бумага).
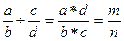 .
. Исходными данными являются четыре целые величины: а, b, с, d. Результат - два целых числа m и n.
Исходными данными являются четыре целые величины: а, b, с, d. Результат - два целых числа m и n.


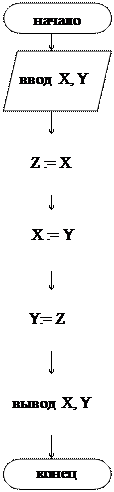
 ввод X,Y
ввод X,Y Y:=Z
Y:=Z
 Результат: x = -7, y = 3.
Результат: x = -7, y = 3.


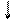

 изменяющимся с шагом 0,5.
изменяющимся с шагом 0,5.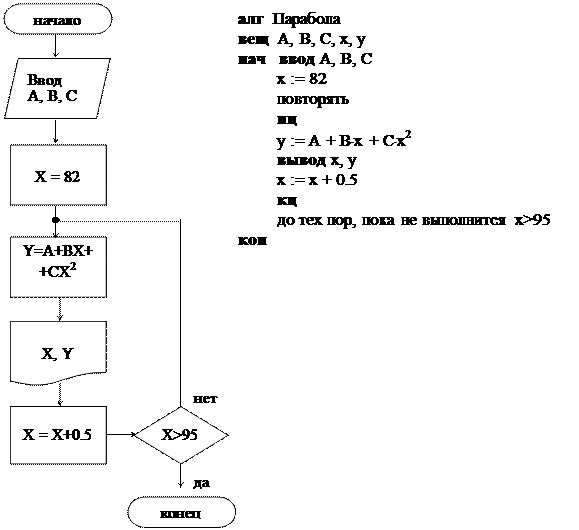
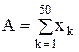 ,
, 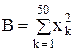 ,
, 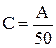 ,
, 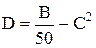
 кц
C:= A/50
B:=B/50 – C2
вывод “значение С=”, С
“значение В=”, В
кон
кц
C:= A/50
B:=B/50 – C2
вывод “значение С=”, С
“значение В=”, В
кон
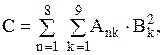 где
где - матрица или двумерный массив данных одного и того же типа
- матрица или двумерный массив данных одного и того же типа
 кц
кц
выводС
кон
кц
кц
выводС
кон
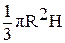 ).
).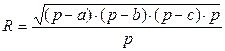 , где
, где 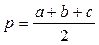 .
.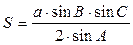 .
. .
.
 , где
, где 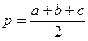 .
.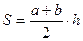 .
. .
.


