
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые равенства и неравенства, их основные свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Билет 1 Определение вычитания натуральных чисел через сложение. Теоретико-множественный смысл разности натуральных чисел. Условие существования разности в множестве натуральных чисел. Правило вычитания числа из суммы и суммы из числа, их теоретико-множественная интерпретация. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл разности натуральных чисел. Натуральные числа — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). Разность целых не отрицательных чисел а - в, называется такое целое неотрицательное число, что: а = в + с. 8 – 6 = 2 т. к. 6 + 2 = 8 С теоретико-множественной позиции разность натуральных чисел a и b представляет собой число элементов в дополнении множества B до множества A, если а = n(A), (целое неотрицательное число определяющее число элементов в множестве А) b = n(B) (целое неотрицательное число определяющее число элементов в множестве В) и B С A (Множество В, является подмножеством множества А). а = n(A)
а – в = n(B \ A) Пример: 7 – 2 = n(B\A) = 5 7 = n(A) 2 = n(B) B С A Условие существования разности натуральных чисел: разность натуральных чисел a и b существует тогда и только тогда, когда b Правило вычитания числа из суммы и суммы из числа, их теоретико-множественная интерпретация. Взаимосвязь вычитания чисел и вычитание множеств позволяет обосновать выбор действия. Чтобы узнать, насколько одно число меньше или больше другого, надо из большего числа вычисть меньшее. Взаимосвязь действий над числами, теоретико-множественный смысл отношений «меньше на и больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями. 1. Вычитание числа из суммы: Правило вычитания числа из суммы: чтобы вычесть число из суммы достаточно вычесть это число из любого слагаемого и полученному результату прибавить оставшееся слагаемое(другое, которое еще не задействовано). Теор.множ.трактовка этого правила: Для трех конечных мн-в А, В и С, таких, что а=n(А), в=n(В) и с=n(С), A имеет место равенство: (А U В) \ С=(А\С) В, из этого следует, что число элементов в этой разности n((А 2.Вычитание суммы из числа: a - (b + c) = a - b - c (при а >= b + c) Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности - второе слагаемое. Теоретико-множественная интерпретация правила вычитания суммы из числа: для трёх конечных множеств А, В, С таких, что a=n(A), b=n(B), c=n(C), B 1. Если из числа вычесть нуль, оно не изменится. 2. Если из числа вычесть это число, получится нуль. 3. Истомина 2 класс, № 370, с. 121
Билет 2 Числовое выражение и выражение с переменной. Тождественные преобразования выражений. Числовые равенства и неравенства, их основные свойства. Примеры тождественных преобразований выражений, выполняемых младшими школьниками при изучении устных приёмов умножения двузначных чисел на однозначные. Числовыми выражениями следует считать такие математические предложения, в записи которых используются числа, знаки действий, скобки. 4 + 2; 37*2; (26 – 3)*4; Результат выполненных действий, указанный в выражении, называется его значением (значением выражения). Среди числовых выражений встречаются такие, значение которых по той или иной причине найти нельзя, такие выражение называются выражениями, не имеющими смысла (4:(3-3)). Если в числовом выражении заменить одно или несколько чисел буквами, то полученное математическое предложение будет называться выражением с переменной (-ыми) (4а-6; 3*а; 3*а + 6). Все те значения переменного, при которых выражение имеет смысл, называются областью определения выражения. *Если f и g являются числовыми выражениями, то f±g; f*g; f:g тоже будут являться числовыми выражениями. Тождественные преобразования выражений. *Два выражения называются тождественно равными, если при любых значениях переменного из области определения этих выражений их соответствующие значения равны. Например, 6*х-3 и 3(2х-1) – выражения тождественно равны. *Переход от одного выражения к другому, который ему тождественно равен, называется тождественным преобразованием выражений (3*(2х-1)=6х-3). К тождественным преобразованиям выражений относятся: - представление числа в виде суммы разрядных слагаемых - раскрытие скобок - вынесение общего множителя за знак скобок - приведение подобных слагаемых - замена результата действий его значением и т.д. Билет 3 Отрезок натурального ряда чисел и счёт элементов конечного множества. Теоретико-множественный смысл натурального числа. Определение отношения «меньше» для натуральных чисел, его теоретико-множественный смысл. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл натурального числа и отношения «меньше». Натуральные числа - числа, используемые при счете. Отрезком натурального ряда чисел Nа называется множество, элементами которого являются все те натуральные числа, которые меньше или равны а: Nа = {1, 2, 3, …., а}Например: отрезок N7 – это множество натуральных чисел, не превосходящих числа 7, т.е. N7 = {1, 2, 3, 4, 5, 6, 7} Свойства отрезка натурального ряда чисел: - каждый отрезок натурального ряда должен содержать «1». - если натуральное число х принадлежит отрезку Nа и х≠а => число, которое следует за х (х+1) будет принадлежать Nа. (х?Nа и х≠а) => (х+1? Nа) Счетом элементов множества А называется установление взаимно однозначного соответствия между элементами данного множества и отрезком натурального ряда Nа. В результате пересчета элементов, входящих в данное множество, мы получаем число, которое можно считать характеристикой численности множества. Взаимно однозначным соответствием между элементами множества X и элементами множества Y называется такое соответствие, при котором каждому элементу из множества X соответствует единственный элемент из множества Y и каждый элемент их множества Y соответсвует единственному элементу из множества Х Множества называются равномощными, если между ними можно установить взаимно однозначное соответствие. Множество является конечным, если оно равномощно некоторому отрезку натурального ряда чисел Nа. Правила счета: 1) Любой элемент из множества может быть назван первым при счете, т.е. пересчитывать элементы можно в любом порядке. 2) Никакой элемент не должен быть пропущен при счете, т.е. должен быть просчитан. 3) Каждый элемент при счете должен быть просчитан только один раз. Любое натуральное число при счёте носит количественный (количество просчитанных элементов) и порядковый (показано, какой элемент был просчитан под этим номером) смысл.
БИЛЕТ № 6 Теоретико-множественный смысл суммы натуральных чисел. Свойства сложения, их теоретико-множественный смысл и назначение. Словесные формулировки свойств сложения, изучаемых в нач школе. Примеры заданий из начального курса математики, раскрывающих теоретико-множественный смысл суммы натуральных чисел. Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Например, если множество А содержит 5 элементов, а множество В – 4 элемента и пересечение множеств А и В, пусто, то число элементов в их объединении равно сумме 5 + 4. Теоретико-множественных позиций сумма натуральных чисел а и в представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а = n(A), b = n(B): а + в = n(A) + n(B) = n(A È B), если А Ç В = Æ. Билет №7 1. Различные определений понятия «квадрат». Свойства и признаки квадрата. Определение понятия «квадрат» в начальном курсе обучения математике и алгоритм его использования при распознавании квадратов. Квадрат – это один из видов геометрических фигур, который подробно изучается в курсе математики в начальной школе. Если говорить о других геометрических фигурах, таких как угол, отрезок, треугольник, круг, то объем содержания, который рассматривается в начальной школе, достаточно узок. В случае же с квадратом, объем, раскрываемых существенных свойств этого понятия значительно более широк. Учащиеся знакомятся с целым рядом существенных свойств указанного понятия, а именно, что у квадрата: - все стороны равны, - все углы равны, - чему равны периметр и площадь квадрата - что квадрат – это вид прямоугольника. Т.к. квадрат – это видовое понятие по отношению к понятиям «четырехугольник», «параллелограмм», «прямоугольник», «ромб», то соответственно квадрату можно давать различные определения в зависимости от родового понятия. Квадрат – это параллелограмм, у которого соседние стороны равны и угол равен 900. Квадрат – это прямоугольник, у которого соседние стороны равны. Квадрат – это ромб, у которого угол равен 900. Квадрат – это четырехугольник, у которого все стороны равны и угол равен 900. Признаки квадрата: 1. если в четырехугольнике все стороны равны и каждый угол равен 900, то этот четырехугольник – квадрат. 2. если в ромбе угол равен 900, то этот ромб – квадрат. 3. если в прямоугольнике соседние стороны равны, то этот прямоугольник – квадрат. Т.к. – это и ромб, и прямоугольник, то он обладает всеми теми свойствами, которые присущи как прямоугольнику, так и ромбу, а т.к. квадрат еще является и параллелограммом, то он обладает и всеми свойствами, присущими параллелограмму. Основные свойства квадрата: 1. диагонали пересекаются под прямым углом 2. диагонали квадрата равны 3. диагонали пересекаются в одной точке и делят его на 4 равных прямоугольных треугольника. 4. площадь равна а2, где а – длина стороны квадрата 5. периметр равен 4а 6. около квадрата можно описать окружность и вписать окружность в него, причем центры вписанной и описанной окружности совпадут. Квадрат относится к одному из тех понятий, которому по определенным методикам дается явное определение, т.е. квадрат определяется как прямоугольник, у которого все стороны равны. Данное определение содержит определенный элемент избыточности, но для осознания детьми данного понятия эта избыточность методически обоснована. Указанное определение лежит в основе распознания объектов, принадлежащих объему понятия квадрат в начальной школе. Для того, чтобы дети распознали, является ли фигура квадратом, надо чтобы они прежде всего определили является ли фигура прямоугольником. Для этого они должны определить, обладает ли фигура следующими свойствами: - является ли она четырехугольником - все ли углы в четырехугольнике прямые - равны ли в прямоугольнике все стороны между собой Если все эти условия выполняются, то фигура является квадратом. Квадрат достаточно часто в курсе математики начальной школы используется в качестве счетного материала на начальном этапе изучения математики. Использование квадрата в таком виде дает возможность создать у ребенка целостное представление о том, что такое квадрат. Является ли фигура квадратом, ребенок определяет визуально. По мере изучения математики у детей расширяется представление о содержании такого понятия как квадрат. Причем следует отметить, что объем рассматриваемых существенных свойств квадрата зависит от того учебника математики, который используется учителем в начальной школе. Но объем некоторых существенных свойств является одинаковым для всех учебников. Объем существенных свойств квадрата, которые должны знать все дети независимо от системы, по которой они занимаются, указан в стандартах по математике для начальной школы. Вот некоторые из них: · это четырехугольник · в квадрате все стороны равны · в квадрате все углы прямые · периметр квадрата · площадь квадрата (а х а) В некоторых учебниках еще рассматриваются такие понятия как: - диагональ квадрата - ось симметрии квадрата.
Билет 8 1. Понятия их объём. Отношения рода и вида между понятиями. Явные и неявные определения понятий. Примеры (2-3) явных и неявных определений понятий, изучаемых в начальном курсе математики. Каждое понятие характеризуется термином, содержанием и объемом. Под объемом понятия следует понимать множество объектов, относящихся к этому понятию. Содержанием понятия называется совокупность всех существенных свойств данного понятия. Следует отметить, что чем больше объем понятия, тем меньше его содержание. Приведем пример: В содержание такого понятия как четырехугольник входят: сумма углов четырехугольника равна 360о и т.п., а в то же время в объем понятия входит множество таких четырехугольников как трапеция, параллелограмм, ромб и т.д. Если взять такое понятие как квадрат, то к объему этого понятия можно отнести только четырехугольники, которые являются квадратами, а в содержание этого понятия входят все свойства четырехугольника, параллелограмма и все свойства специфичные для квадрата (S = a2, диагонали одновременно равны и перпендикулярны). Если объемы понятий совпадают, то такие понятия называют тождественными. Пример: равносторонний треугольник и равноугольный треугольник. * Существенные свойства – это свойства, без которых указанное понятие существовать не может. Одно понятие может определяться через другое, и в этом случае говорят, что эти понятия находятся в отношении рода-вида. Понятие четырехугольника является родовым по отношению к понятию квадрат, а квадрат есть видовое понятие по отношению к четырехугольнику. Видовое понятие обладает всеми свойствами родового понятия. Но нельзя сказать, что родовое понятие обладает всеми свойствами видового понятия. Следует отметить, что одно и то же понятие может быть по отношению к одному родовым, а по отношению к другому видовым. Например: параллелограмм – родовое понятие по отношению к квадрату и видовое понятие по отношению к понятию четырехугольник. А также одно и то же понятие может иметь несколько родовых понятий. Например, для квадрата родовыми понятиями могут быть: параллелограмм, ромб, прямоугольник. Определение – это логическая операция, раскрывающая содержание данного понятия. Определения бывают явные и неявные.
Требования к определению понятий: · В определении должна отсутствовать избыточность, т.е. в определении должно быть указано именно столько существенных свойств определяемого понятия, которых было бы достаточно для распознания объектов, принадлежащих данному объему понятия. Пример: Прямоугольник – это параллелограмм, у которого все углы прямые (достаточно было указать на один прямой угол). · В определении должен отсутствовать порочный круг, т.е. одно понятие не может определяться через другое, которое в свою очередь определяется через первое. Пример: Сложение – это когда числа складываются. · В определении должны быть указаны все свойства, позволяющие однозначно выделять объекты, принадлежащие объему данного понятия. Пример: Прямоугольный треугольник – это такой треугольник, у которого два угла острые, а один нет. Важную роль в курсе математики в начальной школе играют так называемые неявные определения. С помощью этих определений в начальной школе дети получают те или иные представления, знания, умения о математических понятиях. Обычно в начальной школе используют контекстуально-остенсивные определения понятий, используя одновременно рассказ и показ для раскрытия содержания понятия. Пример: углы (Истомина 1 класс), уравнения (Моро 2-3 класс). Истомина 1 класс № 50-51 c. 26 - 27
Билет 9
1. Алгоритм сложения и вычитания многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данных алгоритмов. Одним из основных разделов, изучаемых в курсе математики в начальной школе, является изучение письменных вычислительных приёмов: сложения, вычитания, умножения, деления, называемых алгоритмами сложения, вычитания, умножения и деления. В начальной школе эти алгоритмы известны под: сложением, вычитание, умножением, делением многозначных чисел в столбик. Первым письменным приёмом, изучаемым в курсе математики в начальной школе, являются алгоритмы письменного сложения и вычитания. В основе алгоритмаов письменного сложения и вычитания лежат следующие теоретические положения: 1. Представление числа в десятичной системе счисления. 6145 = 6*103 + 1*102 + 4*10 + 5 Представление числа в десятичной системе счисления аналогом в начальной школе является разрядный состав числа. 2. Предлагая учащимся записать одно слагаемое под другим, а также вычитаемое, разряд под разрядом, мы тем самым раскрываем такие теоретические основы данных алгоритмов, как коммутативно-ассоциативное свойство сложения, а также правило вычитания числа из суммы и суммы из числа. 3. В основе сложения и вычитания многозначных чисел также лежит дистрибутивный закон умножения относительно сложения и вычитания соответственно. 4. Общее положение лежащее в основе данных письменных вычислительных алгоритмов – табличные случаи сложения однозначных чисел. Рассмотрим указанные теоретические положения на конкретных примерах и начнем с письменного сложения: 451 + 237 (представление чисел в десятичной системе счисления) === === (4*102 + 5*10 + 1) + (2*102 + 3*10 + 7) (ассоциативный и коммутативный законы) === (4*102 + 2*102) + (5*10 + 3*10) + (1+7) (дистрибутивный закон умножения относительно сложения) === (4+2)*102 + (5+3)*10 + (1+7) (табличное сложение) === 6*102 + 8*10 + 8 (представление числа в десятичной системе счисления) === 688. Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного сложения многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным сложением многозначных чисел в столбик: Алгоритм письменного сложения многозначных чисел: 1. Записываем второе слагаемое под первым строго разряд под разрядом. 2. Сложение начинаем с разряда единиц: число единиц второго слагаемого прибавляем к числу единиц первого слагаемого. Если полученный результат < 10, записываем его в разряд единиц суммы и переходим к сложению в следующем разряде. Если полученный результат >= 10, то представляем его в виде 10 + c, где с – однозначное число. С записываем в разряд единиц суммы, увеличивая одновременно число единиц в разряде первого десятка на 1. 3. Повторяем один из процессов. 4. Сложение считаем законченным после того, как сложены единицы старших разрядов.
Теперь рассмотрим выше перечисленные теоретические положения на примере письменного вычитания:
=== (4*102 + 6*10 + 8) – (2*102 + 3*10 + 7) (правило вычитания суммы из числа) === (4*102 + 6*10 + 8) – 2*102 – 3*10 – 7 (правило вычитания числа из суммы + дистрибутивное свойство умножения относительно вычитания) === === (4*102 – 2*102) + (6*10 – 3*10) + (8 – 7) (табличное сложение + дистрибутивное свойство умножения относительно вычитания) === 2*102 + 3*10 + 1 (представление числа в десятичной системе счисления) === === 231.
Алгоритм письменного вычитания многозначных чисел: 1. записываем вычитаемое под уменьшаемым строго разряд под разрядом 2. вычитание начинаем с разряда единиц: - если число единиц разряда единиц уменьшаемого больше или равно числу единиц разряда единиц вычитаемого, то производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. - если число единиц разряда единиц уменьшаемого меньше числа единиц разряда единиц вычитаемого и число единиц в разряде десятков уменьшаемого ≠ 0, то уменьшаем число десятков в разряде десятков уменьшаемого на 1, увеличивая одновременно число единиц в разряде единиц уменьшаемого на 10. Производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. - если число единиц в разряде единиц уменьшаемого меньше числа единиц разряда единиц вычитаемого и число единиц в разряде десятков, сотен, тысяч и т.д. = 0, то уменьшаем число единиц в первом из разрядов уменьшаемого, в котором число единиц отлично от 0, на 1, увеличиваем одновременно число единиц в тех разрядах уменьшаемого, где был 0, на 9, а число единиц в разряде единиц на 10. Производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. 3. производим вычитание в следующем разряде, повторяя один из трех описанных процессов 4. процесс вычитания считаем законченным, если произвели вычитание из старшего разряда уменьшаемого. Рассмотрим пункт 2 на конкретном примере:
Изучение алгоритмов письменного сложения и вычитания в курсе математики в начальной школе по разным учебникам происходит в разные периоды (см. Петерсон и Стойлова 2-3 классы).
Билет №10 1. Различные определений понятия «прямоугольник». Свойства и признаки прямоугольника. Определение понятия «прямоугольник» в начальном курсе обучения математике и алгоритм его использования при распознавании квадратов. Прямоугольник – это один из видов геометрических фигур, который подробно изучается в курсе математики в начальной школе. Если говорить о других геометрических фигурах, таких как угол, отрезок, треугольник, круг, то объем содержания, который рассматривается в начальной школе, достаточно узок. В случае же с прямоугольником, объем, раскрываемых существенных свойств этого понятия значительно более широк. Учащиеся знакомятся с целым рядом существенных свойств указанного понятия, а именно, что у квадрата: - противоположные стороны равны - все углы равны 90 градусам - прямые - чему равны периметр и площадь прямоугольника - что прямоугольник – вид четырехугольника Т.к. прямоугольник – это видовое понятие по отношению к понятиям «», «параллелограмм», «четырехугольник», то соответственно прямоугольнику можно давать различные определения в зависимости от родового понятия. Прямоугольник – это параллелограмм, у которого все углы прямые Прямоугольник – это четырехугольник, у которого все углы прямые Признаки прямоугольника: 1. если в четырехугольнике противоположные стороны равны и каждый угол равен 900, то этот четырехугольник – прямоугольник. 2. 4 вершины, 4 стороны, 4 угла,все углы прямые. 3. квадрат -прямоугольник Т.к. – это и четырехугольник и параллелограмм, то он обладает всеми теми свойствами, которые присущи как параллелограмму, так и четырехугольника. Билет 11 1. Определение отношений на множестве. Способы задания отношений. Отношения эквивалентности и их связь с разбиением множества на классы. Отношения порядка. Примеры заданий из учебников математики начальных классов, при выполнении которых происходит: а) разбиение на классы с помощью отношения, б) упорядочение заданных множеств. Отношением на множестве или отношением между элементами множества называется любое подмножество декартова произведения множества самого на себя. Отношение – это есть множество упорядоченных пар. Отношение обозначается заглавными буквами латинского алфавита (конечными). Способы задания отношений. 1) с помощью перечисления входящих в него элементов (только конечное множество). Х = {1; 2; 3; 4; 5; 6} 2) при помощи характеристического свойства (в словесной форме, с помощью формулы). Т: «х больше у на 1» Т: «х = у + 1» 3) графический способ задания: при помощи рисунка, который называется граф.
Т: {(3;2), (4;3), (5;4), (6;5)} Свойства отношений: 1) Отношение R, заданное на множестве X, обладает свойством рефлексивности если каждый элемент данного множества вступает в отношение R с самим собой. На графе это представлено следующим образом: около каждого элемента множества Х присутствует стрелочка.
2) Отношение R, заданное на множестве X, обладает свойством симметричности, если из того, что какой-либо элемент х из множества Х вступает в отношение R с элементом у из множества Х, следует, что элемент у вступает в отношение R с элементом х. На графе: если есть стрелочка от одного элемента к другому, то обязательно имеется стрелочка в обратном направлении. Отношение равенства + между прямыми отношения параллельности и перпендикулярности.
На графе: стрелочка направлена в одну сторону.
Отношения кратности, делимости, больше (меньше) на … 4) Отношение R, заданное на множестве X, обладает свойством транзитивности, если из того, что элемент х из множества Х входит в отношение R с элементом у из множества У и элемент у входит в отношении R с элементом z из множества Х, следует, что элемент х входит в отношение R с элементом z.
Отношения кратности, делимости, параллельности между прямыми. Отношение R, заданное на множестве X называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности. Для того, чтобы выяснить, является ли отношение, заданное на множестве, отношением эквивалентности, достаточно выявить, какими свойствами это отношение обладает. Теорема: Если на множестве Х задано отношение R, которое является отношением эквивалентности, то данное множество при помощи указанного отношения разбивается на классы, которые называются классами эквивалентности. (Считают, что множество Х разбито на классы Х1, Х2, Х3,…Хn, где Х1, Х2, Х3,…Хn – подмножества множества Х, если выполняются 2 условия: 1. подмножества Х1, Х2, Х3,…Хn попарно не пересекаются 2. в объединении дают исходное множество. Если хотя бы одно из этих условий не выполнено, считается, что разбиение на классы не произошло). Верна и обратная теорема: если на множестве задано некоторое отношение, с помощью которого это множество разбивается на классы, то данное отношение будет являться отношением эквивалентности. Указанные теоремы позволяют найти еще один способ проверки того, является ли отношение, заданное на множестве, отношением эквивалентности. Отношение R на множестве X называется отношением порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Множество X называется упорядоченным, если на нем задано отношение порядка. Примеры заданий из учебников математики для начальных классов, при выполнении которых происходит:
X: «х длиннее у»; Х={(а;b); (d;а); (d;b); (d;с); (с;а); (с;b)}]
Билет 12 1. Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Правило установления отношений 2равно», «меньше», «больше» для чисел, записанных в этой системе. Примеры заданий из начального курса математики, при выполнении которых младшие школьники знакомятся с особенностями десятичной системы счисления. Каждый человек постоянно сталкивается в своей жизни с числами, которые он должен уметь записывать, называть, а так же выполнять над ними действия. Основными языком, которым мы пользуемся, для названия записей чисел является позиционная десятичная система счисления. Системой счисления называется язык для названий чисел, их записи, сравнения, а так же выполнения действий над ними. Нумерация чисел – язык для названия чисел их записи и сравнения. Из десяти цифр, которые используются в десятичной системе счисления, составляются конечные последовательности, которые называются краткими записями числа. Система счисления называется позиционной потому что при её использовании значение числа зависит о того на каком месте располагается тот или иной знак (цифра) в записи числа. Десятичной записью числа Х является: Х = а п * 10 п + а п -1 * 10 п -1 +...+ а1 * 10 + а0 а0 = а0 * 10° где а п,а п -1, …, а1, а0 принимают любые из следующих значений: 0, 1, 2, …, 9. Причём а2 не равняется 0 10 п , 10 п -1,…, 10, 10° называются разрядными единицами. (10° = 1) 10 единиц одного разряда составляет одну единицу следующего разряда, поэтому система называется десятичной. Число 10 в этом случае называется основанием системы.
I. единиц II. десятков класс единиц III. IV. тысяч VI. сотен тысяч VII. VIII. класс миллионов IX. Представление натурального числа в десятичной системе счисления: 2382 = 4 * 10³ * 3 * 10 ² + 8 * 10 + 2 Следует отметить, что представление числа в 10 сс. находит своё отражение в несколько адаптированном виде в курсе математики в начальной школе и называется там представлением числа в виде суммы разрядных слагаемых. 4382 = 4000 + 300 + 80 + 2 Представление числа в 10 сс. даёт способ сравнения натуральных чисел, который состоит в следующем: Х = а п * 10 п + а п -1 * 10 п -1 +...+ а1 * 10 + а0 Y = b m * 10 m + b m -1 * 10 m -1 +... + b1 * 10 + b0 Тогда: 1) если n > m, то x > y 2) n = m, то: 1. а п > b m => x > y (5 844 и 3 849, 5 > 3); 2. а п = b m а п -1 = b m -1; а к+ 1 = b к +1 а к > b к => x > y (45 8 23 > 45 8 19) Ознакомление учащихся с особенностями 10 сс. происходит практически в процессе всего обучения математики в курсе начальной школы. Т. е.: - сначала дети знакомятся с этими особенностями на этапе изучения чисел первого десятка; - получают представления о таких понятиях, как разряд единиц. - познания детей расширяется на этапе изучения натуральных чисел и действий над ними в концентре сотни; - вводятся такие понятия и названия как «разря
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 b = n(B)
b = n(B) B С A
B С A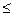 a и эта разница единственна.
a и эта разница единственна.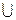 B= Ø, С
B= Ø, С  А
А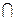 C=
C= 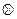 , B
, B 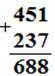 468 – 237 (представление чисел в десятичной системе счисления) ===
468 – 237 (представление чисел в десятичной системе счисления) === Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного вычитания многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным вычитанием многозначных чисел в столбик:
Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного вычитания многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным вычитанием многозначных чисел в столбик: т.к. 3 < 7, то сразу произвести вычитание в разряде единиц мы не можем, т.к. разряды десятков и сотен уменьшаемого содержат по 0 единиц, то уменьшаем число единиц тысяч на 1, увеличивая одновременно число единиц в разрядах, где был 0 на 9, а число единиц в разряде единиц на 10.
т.к. 3 < 7, то сразу произвести вычитание в разряде единиц мы не можем, т.к. разряды десятков и сотен уменьшаемого содержат по 0 единиц, то уменьшаем число единиц тысяч на 1, увеличивая одновременно число единиц в разрядах, где был 0 на 9, а число единиц в разряде единиц на 10.
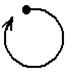 На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости.
На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости.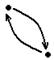
 3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает.
3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает. На графе:
На графе: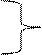 Различают следующие разряды:
Различают следующие разряды: сотен
сотен



