
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истомина Н.Б. 4 класс №580 c. 225Содержание книги
Поиск на нашем сайте
Истомина 1 класс № 50-51 c. 26 - 27
Билет 9
1. Алгоритм сложения и вычитания многозначных чисел в десятичной системе счисления; теоретические факты, лежащие в основе. Примеры заданий из учебников математики для начальной школы, раскрывающих теоретические основы данных алгоритмов. Одним из основных разделов, изучаемых в курсе математики в начальной школе, является изучение письменных вычислительных приёмов: сложения, вычитания, умножения, деления, называемых алгоритмами сложения, вычитания, умножения и деления. В начальной школе эти алгоритмы известны под: сложением, вычитание, умножением, делением многозначных чисел в столбик. Первым письменным приёмом, изучаемым в курсе математики в начальной школе, являются алгоритмы письменного сложения и вычитания. В основе алгоритмаов письменного сложения и вычитания лежат следующие теоретические положения: 1. Представление числа в десятичной системе счисления. 6145 = 6*103 + 1*102 + 4*10 + 5 Представление числа в десятичной системе счисления аналогом в начальной школе является разрядный состав числа. 2. Предлагая учащимся записать одно слагаемое под другим, а также вычитаемое, разряд под разрядом, мы тем самым раскрываем такие теоретические основы данных алгоритмов, как коммутативно-ассоциативное свойство сложения, а также правило вычитания числа из суммы и суммы из числа. 3. В основе сложения и вычитания многозначных чисел также лежит дистрибутивный закон умножения относительно сложения и вычитания соответственно. 4. Общее положение лежащее в основе данных письменных вычислительных алгоритмов – табличные случаи сложения однозначных чисел. Рассмотрим указанные теоретические положения на конкретных примерах и начнем с письменного сложения: 451 + 237 (представление чисел в десятичной системе счисления) === === (4*102 + 5*10 + 1) + (2*102 + 3*10 + 7) (ассоциативный и коммутативный законы) === (4*102 + 2*102) + (5*10 + 3*10) + (1+7) (дистрибутивный закон умножения относительно сложения) === (4+2)*102 + (5+3)*10 + (1+7) (табличное сложение) === 6*102 + 8*10 + 8 (представление числа в десятичной системе счисления) === 688. Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного сложения многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным сложением многозначных чисел в столбик: Алгоритм письменного сложения многозначных чисел: 1. Записываем второе слагаемое под первым строго разряд под разрядом. 2. Сложение начинаем с разряда единиц: число единиц второго слагаемого прибавляем к числу единиц первого слагаемого. Если полученный результат < 10, записываем его в разряд единиц суммы и переходим к сложению в следующем разряде. Если полученный результат >= 10, то представляем его в виде 10 + c, где с – однозначное число. С записываем в разряд единиц суммы, увеличивая одновременно число единиц в разряде первого десятка на 1. 3. Повторяем один из процессов. 4. Сложение считаем законченным после того, как сложены единицы старших разрядов.
Теперь рассмотрим выше перечисленные теоретические положения на примере письменного вычитания:
=== (4*102 + 6*10 + 8) – (2*102 + 3*10 + 7) (правило вычитания суммы из числа) === (4*102 + 6*10 + 8) – 2*102 – 3*10 – 7 (правило вычитания числа из суммы + дистрибутивное свойство умножения относительно вычитания) === === (4*102 – 2*102) + (6*10 – 3*10) + (8 – 7) (табличное сложение + дистрибутивное свойство умножения относительно вычитания) === 2*102 + 3*10 + 1 (представление числа в десятичной системе счисления) === === 231.
Алгоритм письменного вычитания многозначных чисел: 1. записываем вычитаемое под уменьшаемым строго разряд под разрядом 2. вычитание начинаем с разряда единиц: - если число единиц разряда единиц уменьшаемого больше или равно числу единиц разряда единиц вычитаемого, то производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. - если число единиц разряда единиц уменьшаемого меньше числа единиц разряда единиц вычитаемого и число единиц в разряде десятков уменьшаемого ≠ 0, то уменьшаем число десятков в разряде десятков уменьшаемого на 1, увеличивая одновременно число единиц в разряде единиц уменьшаемого на 10. Производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. - если число единиц в разряде единиц уменьшаемого меньше числа единиц разряда единиц вычитаемого и число единиц в разряде десятков, сотен, тысяч и т.д. = 0, то уменьшаем число единиц в первом из разрядов уменьшаемого, в котором число единиц отлично от 0, на 1, увеличиваем одновременно число единиц в тех разрядах уменьшаемого, где был 0, на 9, а число единиц в разряде единиц на 10. Производим вычитание, полученный результат записываем в разряд единиц разности и переходим к вычитанию в следующем разряде. 3. производим вычитание в следующем разряде, повторяя один из трех описанных процессов 4. процесс вычитания считаем законченным, если произвели вычитание из старшего разряда уменьшаемого. Рассмотрим пункт 2 на конкретном примере:
Изучение алгоритмов письменного сложения и вычитания в курсе математики в начальной школе по разным учебникам происходит в разные периоды (см. Петерсон и Стойлова 2-3 классы).
Билет №10 1. Различные определений понятия «прямоугольник». Свойства и признаки прямоугольника. Определение понятия «прямоугольник» в начальном курсе обучения математике и алгоритм его использования при распознавании квадратов. Прямоугольник – это один из видов геометрических фигур, который подробно изучается в курсе математики в начальной школе. Если говорить о других геометрических фигурах, таких как угол, отрезок, треугольник, круг, то объем содержания, который рассматривается в начальной школе, достаточно узок. В случае же с прямоугольником, объем, раскрываемых существенных свойств этого понятия значительно более широк. Учащиеся знакомятся с целым рядом существенных свойств указанного понятия, а именно, что у квадрата: - противоположные стороны равны - все углы равны 90 градусам - прямые - чему равны периметр и площадь прямоугольника - что прямоугольник – вид четырехугольника Т.к. прямоугольник – это видовое понятие по отношению к понятиям «», «параллелограмм», «четырехугольник», то соответственно прямоугольнику можно давать различные определения в зависимости от родового понятия. Прямоугольник – это параллелограмм, у которого все углы прямые Прямоугольник – это четырехугольник, у которого все углы прямые Признаки прямоугольника: 1. если в четырехугольнике противоположные стороны равны и каждый угол равен 900, то этот четырехугольник – прямоугольник. 2. 4 вершины, 4 стороны, 4 угла,все углы прямые. 3. квадрат -прямоугольник Т.к. – это и четырехугольник и параллелограмм, то он обладает всеми теми свойствами, которые присущи как параллелограмму, так и четырехугольника.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.25 (0.008 с.) |

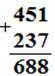 468 – 237 (представление чисел в десятичной системе счисления) ===
468 – 237 (представление чисел в десятичной системе счисления) === Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного вычитания многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным вычитанием многозначных чисел в столбик:
Для того, чтобы упростить указанную запись, которая представляет собой алгоритм письменного вычитания многозначных чисел, предлагается представить эту запись в следующем виде, называя его письменным вычитанием многозначных чисел в столбик: т.к. 3 < 7, то сразу произвести вычитание в разряде единиц мы не можем, т.к. разряды десятков и сотен уменьшаемого содержат по 0 единиц, то уменьшаем число единиц тысяч на 1, увеличивая одновременно число единиц в разрядах, где был 0 на 9, а число единиц в разряде единиц на 10.
т.к. 3 < 7, то сразу произвести вычитание в разряде единиц мы не можем, т.к. разряды десятков и сотен уменьшаемого содержат по 0 единиц, то уменьшаем число единиц тысяч на 1, увеличивая одновременно число единиц в разрядах, где был 0 на 9, а число единиц в разряде единиц на 10.


