
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства прямоугольникаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Диагонали прямоугольника равны. 2. диагонали прямоугольника равны 3. диагонали пересекаются в одной точке и делят его на 4 равных треугольника. 4. площадь равна S=a*b, где а – длина стороны прямоугольника, a b - ширина 5. периметр равен = a+b+a+b Прямоугольник относится к одному из тех понятий, которому по определенным методикам дается явное определение, т.е. прямоугольник определяется как, четырехугольник у которого все углы прямые. Указанное определение лежит в основе распознания объектов, принадлежащих объему понятия прямоугольник в начальной школе. Для того, чтобы дети распознали, является ли фигура прямоугольником, надо чтобы они прежде всего определили является ли фигура четырехугольником Для этого они должны определить, обладает ли фигура следующими свойствами: - все ли углы в четырехугольнике прямые - равны ли в прямоугольнике противоположные стороны между собой Если все эти условия выполняются, то фигура является прямоугольником
Билет 11 1. Определение отношений на множестве. Способы задания отношений. Отношения эквивалентности и их связь с разбиением множества на классы. Отношения порядка. Примеры заданий из учебников математики начальных классов, при выполнении которых происходит: а) разбиение на классы с помощью отношения, б) упорядочение заданных множеств. Отношением на множестве или отношением между элементами множества называется любое подмножество декартова произведения множества самого на себя. Отношение – это есть множество упорядоченных пар. Отношение обозначается заглавными буквами латинского алфавита (конечными). Способы задания отношений. 1) с помощью перечисления входящих в него элементов (только конечное множество). Х = {1; 2; 3; 4; 5; 6} 2) при помощи характеристического свойства (в словесной форме, с помощью формулы). Т: «х больше у на 1» Т: «х = у + 1» 3) графический способ задания: при помощи рисунка, который называется граф.
Т: {(3;2), (4;3), (5;4), (6;5)} Свойства отношений: 1) Отношение R, заданное на множестве X, обладает свойством рефлексивности если каждый элемент данного множества вступает в отношение R с самим собой. На графе это представлено следующим образом: около каждого элемента множества Х присутствует стрелочка.
2) Отношение R, заданное на множестве X, обладает свойством симметричности, если из того, что какой-либо элемент х из множества Х вступает в отношение R с элементом у из множества Х, следует, что элемент у вступает в отношение R с элементом х. На графе: если есть стрелочка от одного элемента к другому, то обязательно имеется стрелочка в обратном направлении. Отношение равенства + между прямыми отношения параллельности и перпендикулярности.
На графе: стрелочка направлена в одну сторону.
Отношения кратности, делимости, больше (меньше) на … 4) Отношение R, заданное на множестве X, обладает свойством транзитивности, если из того, что элемент х из множества Х входит в отношение R с элементом у из множества У и элемент у входит в отношении R с элементом z из множества Х, следует, что элемент х входит в отношение R с элементом z.
Отношения кратности, делимости, параллельности между прямыми. Отношение R, заданное на множестве X называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности. Для того, чтобы выяснить, является ли отношение, заданное на множестве, отношением эквивалентности, достаточно выявить, какими свойствами это отношение обладает. Теорема: Если на множестве Х задано отношение R, которое является отношением эквивалентности, то данное множество при помощи указанного отношения разбивается на классы, которые называются классами эквивалентности. (Считают, что множество Х разбито на классы Х1, Х2, Х3,…Хn, где Х1, Х2, Х3,…Хn – подмножества множества Х, если выполняются 2 условия: 1. подмножества Х1, Х2, Х3,…Хn попарно не пересекаются 2. в объединении дают исходное множество. Если хотя бы одно из этих условий не выполнено, считается, что разбиение на классы не произошло). Верна и обратная теорема: если на множестве задано некоторое отношение, с помощью которого это множество разбивается на классы, то данное отношение будет являться отношением эквивалентности. Указанные теоремы позволяют найти еще один способ проверки того, является ли отношение, заданное на множестве, отношением эквивалентности. Отношение R на множестве X называется отношением порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Множество X называется упорядоченным, если на нем задано отношение порядка. Примеры заданий из учебников математики для начальных классов, при выполнении которых происходит:
X: «х длиннее у»; Х={(а;b); (d;а); (d;b); (d;с); (с;а); (с;b)}]
Билет 12 1. Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Правило установления отношений 2равно», «меньше», «больше» для чисел, записанных в этой системе. Примеры заданий из начального курса математики, при выполнении которых младшие школьники знакомятся с особенностями десятичной системы счисления. Каждый человек постоянно сталкивается в своей жизни с числами, которые он должен уметь записывать, называть, а так же выполнять над ними действия. Основными языком, которым мы пользуемся, для названия записей чисел является позиционная десятичная система счисления. Системой счисления называется язык для названий чисел, их записи, сравнения, а так же выполнения действий над ними. Нумерация чисел – язык для названия чисел их записи и сравнения. Из десяти цифр, которые используются в десятичной системе счисления, составляются конечные последовательности, которые называются краткими записями числа. Система счисления называется позиционной потому что при её использовании значение числа зависит о того на каком месте располагается тот или иной знак (цифра) в записи числа. Десятичной записью числа Х является: Х = а п * 10 п + а п -1 * 10 п -1 +...+ а1 * 10 + а0 а0 = а0 * 10° где а п,а п -1, …, а1, а0 принимают любые из следующих значений: 0, 1, 2, …, 9. Причём а2 не равняется 0 10 п , 10 п -1,…, 10, 10° называются разрядными единицами. (10° = 1) 10 единиц одного разряда составляет одну единицу следующего разряда, поэтому система называется десятичной. Число 10 в этом случае называется основанием системы.
I. единиц II. десятков класс единиц III. IV. тысяч
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.85.96 (0.008 с.) |


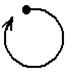 На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости.
На множестве натуральных чисел рефлексивными свойствами обладают отношения кратности, равенства, делимости.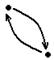
 3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает.
3) Отношение R, заданное на множестве X, обладает свойством антисимметричности, если для различных элементов х и у из множества X из того, что элемент х вступил в отношение R с элементом у следует, что элемент у в отношение R с элементом х не вступает. На графе:
На графе: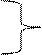 Различают следующие разряды:
Различают следующие разряды: сотен
сотен


