Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение трапеции. Виды трапеции. Свойства равнобедренной трапеции.Содержание книги
Поиск на нашем сайте
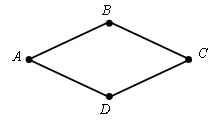
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны Виды трапеции: равнобедренная и прямоугольная Первое свойство равнобедренной трапеции – у равнобедренной трапеции боковые стороны равны Второе свойство равнобедренной трапеции – у равнобедренно трапеции углы при основании равны
Определение прямоугольника. Свойство прямоугольника. Признак прямоугольника. Прямоугольник – параллелограмм, у которого все углы прямые Свойство прямоугольника – диагонали прямоугольника равны Признак прямоугольника – если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
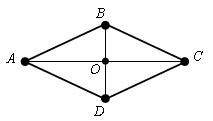
Определение ромба. Свойство ромба. Ромб – параллелограмм, у которого все стороны равны Свойство ромба – диагонали ромба взаимно перпендикулярны и делят его углы пополам
Определение квадрата. Свойства квадрата. Квадрат – прямоугольник, у которого все стороны равны Первое свойство квадрата – все углы квадрата прямые Второе свойство квадрата – диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам
Понятие площади многоугольника. Единица измерения площадей. Свойства площадей. Площадь квадрата.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник Единицы измерения площадей: квадратный сантиметр (см2), квадратный метр (м2), квадратный миллиметр (мм2) и т. д. Первое свойство площади – равные многоугольники имеют равные площади Второе свойство площади – если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников Площадь квадрата – площадь квадрата равна квадрату его стороны (S=a2)
Определение высоты параллелограмма. Площадь параллелограмма. Высота параллелограмма – перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание Площадь параллелограмма –
произведение основания на высоту
произведение сторон на синус угла между ними
полупроизведение диагоналей на синус угла между ними
Определение высоты трапеции. Площадь трапеции.
Высота трапеции – перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. Площадь трапеции – площадь трапеции равна произведению полусуммы её оснований на высоту S=
произведение средней линии на высоту
полупроизведение диагоналей на синус угла между ними
Площадь ромба (через диагонали). Площадь прямоугольника. Площадь ромба – площадь ромба равна половине произведений его диагоналей
Площадь прямоугольника – площадь прямоугольника равна произведению его смежных сторон S=ab
Теорема Пифагора и обратная ей. Теорема Пифагора – в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2 Теорема, обратная теореме Пифагора – если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный Площадь прямоугольного треугольника. Теорема об отношениях площадей треугольников: с равными высотами; имеющих по равному углу. Площадь прямоугольного треугольника – площадь прямоугольного треугольника равна половине произведения его катетов Теорема об отношениях площадей треугольников имеющих по равному углу – если угол одного треугольника равен углу другого, то площади треугольников относятся как произведение сторон, заключающих равные углы Теорема об отношениях площадей треугольников с равными высотами – если площади двух треугольников равны, то их площади относятся как основания
Определение подобных треугольников. Теоремы об отношениях периметров и площадей подобных треугольников. Подобные треугольники – два треугольника, углы которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого Теорема об отношении площади подобных треугольников – отношение площадей подобных треугольников равно квадрату коэффициента подобия
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.006 с.) |












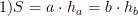


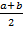 h
h