Сформулируйте теорему об окружности, вписанной в треугольник.

Теорема. В любой треугольник можно вписать окружность.

 

Сколько окружностей можно вписать в треугольник?

В треугольник можно вписать только одну окружность.

Какая точка является центром окружности, вписанной в треугольник?

Центром окружности, вписанной в треугольник, является точка пересечения биссектрис углов треугольника.

 

Как построить окружность, вписанную в треугольник? Можно ли вписать окружность в четырёхугольник?

1) Построить биссектрисы двух углов треугольника.

2) Точку их пересечения обозначить буквой О.

3) Из точки О к одной из сторон треугольника провести перпендикуляр.

4) Построить окружность с центром в точке О и радиусом, равным проведённому перпендикуляру.

5) Не во всякий четырёхугольник можно вписать окружность

 

В какой четырёхугольник можно вписать окружность?

Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

АВ+СD=ВС+АD

 

Можно ли вписать окружность в ромб? квадрат? параллелограмм? прямоугольник? трапецию?

1) В ромбе и в квадрате все стороны равны, значит и суммы противоположных сторон равны, поэтому в любой ромб и в любой квадрат можно вписать окружность.

2) В параллелограмм только тогда можно вписать окружность, когда он будет ромбом.

3) В прямоугольник только тогда можно вписать окружность, когда он будет квадратом.

4) В трапецию можно вписать окружность тогда, когда суммы противоположных сторон будут равны.

 

Каким свойством обладают стороны четырёхугольника, описанного около окружности?

В любом описанном четырёхугольнике суммы противоположных сторон равны.

 

АВ+СD=ВС+АD

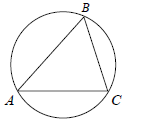
Какая окружность называется описанной около треугольника? Какой треугольник называется вписанным в окружность?

Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник – вписанным в эту окружность.

 

 

Какая окружность называется описанной около многоугольника? Какой многоугольник называется вписанным в окружность?

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

 

 

Сформулируйте теорему об окружности, описанной около треугольника.

Теорема: Около любого треугольника можно описать окружность.

 

 

Сколько окружностей можно описать около данного треугольника?

Около треугольника можно описать только одну окружность.

 

Какая точка является центром окружности, описанной около треугольника?

Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.

 

 

Где находится центр окружности, описанной около остроугольного треугольника?

Центр окружности, описанной около остроугольного треугольника лежит внутри треугольника.

 

Как построить окружность, описанную около остроугольного треугольника?

1) Построить серединные перпендикуляры к двум сторонам треугольника.

2) Точку их пересечения обозначить буквой О.

3) Построить окружность с центром в точке О и радиусом, равным расстоянию от точки О до любой из вершин треугольника.

 

Где находится центр окружности, описанной около прямоугольного треугольника?

Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.

 

Как построить окружность, описанную около прямоугольного треугольника?

1 способ:

1) Построить серединные перпендикуляры к двум сторонам треугольника.

2) Точку их пересечения обозначить буквой О (точка О – середина гипотенузы).

3) Построить окружность с центром в точке О и радиусом, равным расстоянию от точки О до любой из вершин треугольника.

2 способ:

1) Построить точку О – середину гипотенузы.

2) Построить окружность с центром в точке О и радиусом, равным половине гипотенузы.

 

 

Где находится центр окружности, описанной около тупоугольного треугольника?

Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.