Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производство материальных благ и производственная функция.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В кругообороте капитала второй стадией является производство - процесс взаимодействия факторов производства (ресурсов) с целью получения новых благ и услуг, необходимых потребителям. С точки зрения марксизма производство рассматривается как процесс создания и возрастания стоимости, первоначально авансированного капитала, создания прибыли (прибавочной стоимости). Производственный процесс можно описать с помощью производственной функции. Зависимость максимального объема производимого продукта от затрат, используемых факторов называется производственной функцией: Q=f(K,L,M), где К - затраты капитала; L - затраты труда; М - затраты материалов, сырья; Q - максимальный объем производства при заданной технологии и определенных факторах производства. Если производителю известна производственная функция и его затраты, то он легко может получить прогноз объема своей продукции. Для укрупненного анализа и прогнозирования используется производственная функция Кобба-Дугласа: Q=k×Ka×Lb×Mg, где k - коэффициент пропорциональности или масштабности; a, b, g - коэффициенты объема производства соответственно по капиталу, труду, материалам или коэффициенты прироста Q, приходящиеся на 1 % прироста соответствующего фактора (a+b+g=1). Общие свойства производственной функции, хотя для производства каждого конкретного продукта требуется сочетание разных факторов: - взаимодополняемость факторов, т.е. набор определенных факторов, (отсутствие одного из них означает невозможность производства); - определенная взаимозаменяемость факторов, т.е. один фактор может быть заменен другим в определенной пропорции (труд на средства производства, и наоборот), но не означает полного исключения из производственного процесса какого-либо фактора. 3.1 Производственная функция с одним переменным ресурсом. Закон убывающей производительности (отдачи) Различные комбинации факторов производства дают разные объемы произведенной продукции. Однако существует определенный предел роста объема производства при увеличении одного фактора, в то время как остальные факторы остаются постоянными. Это свойство получило название закона убывающей производительности, или убывающей отдачи: новые дополнительные затраты одного фактора при неизменности остальных дают все меньший объем дополнительной продукции. Этот закон характерен для производственной функции с одним переменным фактором: Q=f(х, у), где у(затраты капитала) - const, х (затраты труда) - величина переменного фактора. Прежде чем, перейти к анализу данной функции, необходимо ввести ряд понятий общего, среднего и придельного продуктов. Общий (физический) продукт (ТР) - общее количество произведенного фирмой продукта, измеряемого в физических единицах (кг, т, л), которое изменяется по мере увеличения использования переменного фактора ТР=Q=f(K,L,M). Средний (физический) продукт (АР) - это отношение общего продукта к количеству использованного в производстве переменного фактора (Qxres=xres):
Предельный (физический) продукт (МР) - это количество дополнительного продукта, полученное при использовании дополнительной единицы переменного ресурса (при неизменности других затрат)
На кривой ТР отмечены три точки: В - точка перегиба, где MP достигает своего максимального значения, где TP=maxMP. С - точка, которая принадлежит касательной (0К), совпадающей с линией соединяющей данную точку с началом координат, где MP=maxAP D - точка максимального значения ТР (maxTP) при MP=0. Точка А движется по кривой ТР, соединив точку А с началом координат, получим линию ОА, а опустив перпендикуляр на ось абсцисс, получим DОАМ, где
Проведя через точку А касательную, получим угол b.
Сравнивая два треугольника LAM и OAM видно, что до определенного момента tg b>tg a, следовательно МР>АР. Когда точка А совпадает с точкой В, tg b имеет максимальное значение, следовательно МР достигает максимального значения(maxMP). Когда точка А совпадает с точкой С, то МР=maxАР. При
с одним переменным фактором: а) кривая общего продукта (ТР) изменяется в зависимости от величины переменного фактора; б) кривая среднего (АР) и предельного (МР) продукта. Сравнивая два треугольника LAM и OAM видно, что до определенного момента tg b>tg a, следовательно МР>АР. Когда точка А совпадает с точкой В, tg b имеет максимальное значение, следовательно МР достигает максимального значения(maxMP). Когда точка А совпадает с точкой С, то МР=maxАР. При дальнейшем увеличении фактора Х, tgb будет уменьшаться и при совпадении точки А с точкой D будет равен 0, где maxTP при МР=0. Далее TP будет уменьшаться, а MP примет отрицательное значение. Из приведенного анализа можно сделать вывод, что наиболее эффективно используется переменный фактор (Х) на отрезке BC(от точки B, где TP=maxMP до точки C где MP=maxAP): на каждую дополнительную единицу затраченного переменного фактора производитель получает наибольший прирост общего продукта (ТР). После того, как AP достигает своего максимального значения, эффективность увеличения переменного фактора в производстве снижается. Примером производственной функции с одним переменным фактором служит производство фермером, какого-либо продукта. Все факторы производства: величина земельных угодий, сельхозтехники, посевного материала, количество труда - остаются из года в год постоянной величиной. Изменяется лишь один фактор - количество применяемых удобрений. Следовательно, в результате изменяется величина получаемого продукта: TP сначала быстро растет, затем рост ТР замедляется, и начинает убывать. Дальнейшее увеличение переменного фактора (удобрений) не дает увеличения продукта (ТР). Если бесконечно увеличивать применение минеральных удобрений, то весь урожай будет недостаточен для того, чтобы накормить страну.
3.2 Производственная функция с двумя переменными ресурсами. Изокванта и предельная норма технологическогозамещения (MRTSx,y)
Рассмотрим производственную функцию, где переменными являются два фактора производства, которые при определенном сочетании дают в результате один объем производимого продукта. При этом возрастание одного фактора вызывает уменьшение другого таким образом, что общий объем производства остается на прежнем уровне. Эту зависимость можно представить графически с использованием изокванты - это кривая равного продукта, отражающая все возможные комбинации двух факторов, которые могут быть использованы для производства определенного объема продукта. С увеличением объемов используемых переменных факторов возникает возможность выпуска большего объема продукции, поэтому изокванта, отражающая производство большего объема продукта расположена правее и выше предыдущей. Разным объемам выпускаемой продукции соответствует множество изоквант, которые образуют карту изоквант.
Рисунок 6.3 Изокванта, отражающая производственную функцию с двумя переменными факторами Рисунок 6.4. Карта изоквант
Изокванты, отражающие ситуацию в сфере производства, подобны кривым безразличия, которые отражают ситуацию в сфере потребления; Отрицательный наклон изоквант объясняется тем, что увеличение одного фактора при определенном объеме выпуска продукта сопровождается уменьшением количества другого фактора. Крутизна наклона изокванты характеризуется предельной нормой технологического замещения (
Рисунок 6.5 Определение MRTSx,y через касательную к изокванте и изменение MRTSx,y при движении вниз по изокванте При движении вниз по изокванте значение В реальных производственных процессах встречаются два исключительных случая в конфигурации изоквант. Эта ситуация, когда факторы идеально взаимозаменяемы (полная автоматизация производства), то
Рисунок 6.6 Изокванта а - при полной заменяемости факторов; б - при жесткой дополняемости факторов Так, при полной автоматизации производства(рис 6.6 а) в точке А весь производственный процесс будет состоять из затрат капитала, в точке В машины будут заменены рабочими руками, а в точках С и D капитал и труд будут дополнять друг друга. В другом случае (рис 6.6 б), как например, в таксопарке, чтобы увеличить Q1 до Q2, т.е. объем (количество) обслуживаемых пассажиров, надо увеличить количество машин и численность водителей. 3.3 Эффект масштаба производства Главная проблема любой экономики - проблема эффективности, отсюда возникает вопрос, что эффективнее один крупный завод или несколько мелких предприятий? Плановая экономика всегда отвечала однозначно, отдавая приоритет промышленным гигантам. С переходом к рыночной экономике стали повсеместно разукрупнять предприятия. А хорошо ли это? Где же золотая середина? Доказательный ответ на заданный вопрос можно получить исследовав эффект масштаба производства, т.е. эффект от расширения производства при изменении всех факторов (ресурсов). Предположим, что обувная фабрика приняла решение значительную часть прибыли направить на развитие производства с целью увеличения объемов производимой продукции. При этом капитал (оборудование, станки, производственные площади) увеличен в 2 раза, численность работников - тоже в 2 раза. Что же при этом произойдет с объемом выпускаемой продукции? Возможны 3 варианта ответа:
- количество продукции (Q) возрастает в 2 раза (постоянная отдача от масштаба производства, рис 6.7 а); - Q возрастает, но меньше, чем в 2 раза (убывающая отдача от масштаба производства, рис 6.7 б); - Q возрастает более, чем в 2 раза (возрастающая отдача от масштаба производства, рис 6.7 в). а – постоянная отдача от масштаба; б – убывающая отдача от масштаба; в – возрастающая отдача от масштаба Постоянная отдача от масштаба производства объясняется однородностью переменных факторов: при пропорциональном увеличении капитала и труда на таком производстве средняя и предельная производительность этих факторов остается неизменной. В таком случае безразлично, будет ли работать одно крупное предприятие или вместо него будет создано два мелких. При убывающей отдаче невыгодно создавать крупное производство. Причиной низкой эффективности в таком случае являются дополнительные затраты, связанные с управлением подобным производством, сложности координации крупного производства. Возрастающая отдача от масштаба производства характерна для тех производств, где возможна широкая автоматизация производственных процессов, применение поточных и конвейерных линий. Но с тенденцией возрастающей отдачи от масштаба нужно быть очень осторожным, так как рано или поздно она превращается в постоянную, а затем и убывающую отдачу от масштаба.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.78.107 (0.012 с.) |

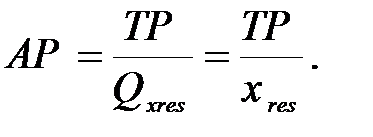

 (разница между последующим и предыдущим значением ТР).
(разница между последующим и предыдущим значением ТР).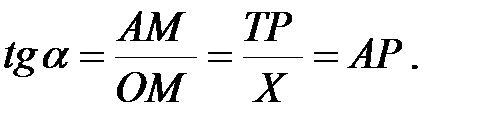

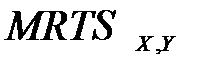 )
)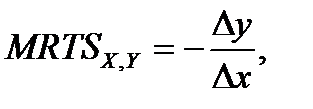 т.е. измеряется соотношением изменения фактора y к изменению фактора x, и показывает на сколько нужно увеличить объем одного ресурса, чтобы уменьшить объем другого ресурса на одну единицу при заданном объеме выпуска. Поскольку замена факторов происходит в обратном отношении, то MRTSx,y берется со знаком минус.
т.е. измеряется соотношением изменения фактора y к изменению фактора x, и показывает на сколько нужно увеличить объем одного ресурса, чтобы уменьшить объем другого ресурса на одну единицу при заданном объеме выпуска. Поскольку замена факторов происходит в обратном отношении, то MRTSx,y берется со знаком минус.